基于马氏链的文献评价修正模型

刘 圣，张景肖

（中国人民大学 统计学院，北京 100872）

0 引言

在国内，现在应用最广泛的科研评价指标的数据源是科学引文索引数据库(SCI)，SCI是由美国科学情报所(ISI)建立的国际性数据库，它收录了国际上高质量的学术期刊，建立了较为科学的文献计量指标，并且被越来越多地用于评价各国的科研绩效。尽管SCI在国际范围内得到了广泛的应用，其本身仍存在很多局限性，不能很好地反映文献的学术水平。

基于马氏链的文献评价方法是对传统文献计量指标（期刊影响因子）的修正和完善，主要包括迭代影响因子(Pinski和 Narin,1976)和 Page Rank算法(Page et al,1998)，该方法能够解决传统文献计量指标对不同的引用关系不进行区分的问题，可以更好地描述文献的影响力，因而也越来越受到研究人员的关注。因为计算过程相对复杂，这类方法在实际中的应用远没有传统计量指标广泛，但该方法对著名的搜索引擎算法的产生起到了重要影响，Larry Page和Sergey Brin提出的Page Rank算法是迭代影响因子在Web结构上的应用(Cole,2007)。

根据文章间的引用与网页间链接的相似性，将发展相对更加成熟的网页排序方法 （如Page Rank算法和HITS算法等）应用到文献的引文分析中是一项重大创新，具有很强的实用价值(Langville和Meyer 2006)。但是基于马氏链的文献评价模型在理论模型、实际应用中仍有许多需要改进和完善的地方，如马氏链转移矩阵中的等权重问题：不同的参考文献对文章的影响是不同的，显然不应同等对待；模型参数敏感性问题：不同的参数选择会导致不同的评价结果，如何选择最优的参数值仍有待研究。本文将针对这些问题提出修正模型，使得修正后的模型结果更能反映实际情况。

1 基于马氏链的文献评价模型

基于马氏链的文献评价方法的思路可描述如下：该方法模拟一名研究人员查阅文献的过程，将所有待评价的文献看作马氏链的状态空间，其中每一篇待评价文献作为一个状态，状态转移矩阵则是根据文献间是否有引用关系、引用关系的类型强弱决定的。文献的影响力则用研究人员在每篇文献上的平均停留次数或到达每篇文献的概率来度量，即需要求解该马氏链的平稳分布，记为 R=（PR(p1)，PR(p2)，…，PR(pN)）T。该模型可表示如下：

其中：p1，p2，…，pN为待评文献；

d为阻尼因子(damping factor)，通常取为0.85；

B(pi)为文献pi的引用文献，即引用的文献；

|O(pj)|为文献pj的参考文献数目。

2 基于马氏链的文献评价修正模型

虽然上述基于引文结构的文献评价较之传统的评价指标有了某种程度的改进，并且随着信息技术的发展，该方法在实际中也有越来越多的应用。但是，从已经发表的相关研究中可以看出，现有的研究主要是从网页链接和引文网络的共同之处出发，借用网页评价中的算法，并没有考虑文献引文网络的独有特点和专有信息。引文结构只代表了文献信息的一部分，所以基于马氏链的文献评价方法仍存在进一步完善的空间。本文将从这个角度出发，研究更加合理的文献评价模型。

2.1 文献相似度指标的引入及转移矩阵的修正

在构造马氏链转移矩阵时，我们最初都是假定等权重的，即被同一篇文章所引用的文章是同等重要的。但很多情况是：一篇文章所引用的文章中有一部分起着非常重要的作用，而另一些只是补充性材料。因此，为了提高文献排序的准确性，有必要对文献的不同引用关系进行区分。

在修正模型中，我们创新性地在文献评价模型中提出了文献引用动机的概念，利用文献引用动机来反映文献间的引文关系，并根据不同的引用动机分配马氏链中的转移概率。对引文动机的研究，除了从引文网络的结结构出发，文献的标题、关键词和摘要等同样包含文献的重要信息，我们试图通过这些信息对文献引用的动机、引文的贡献进行度量。我们将综合考虑引文结构和文献的标题、摘要和关键词等文献信息，对文献进行评价。

引文分析的所有结果都是基于一个基本假定：引用文献对被引文献的引用是对被引文献的影响力的肯定。但是文献的引用情况十分复杂，并不是所有的引用都是对被引文献影响力的肯定。Eugene Garfield,Brooks,Oppenheim等诸多学者都对于引用情况问题有相关研究，对引用情况进行了不同类型的分类总结。

Brooks(1986)根据前人的研究，将引文的动机分为七类：

(1)新颖性：只引用最新的资料，以彰显自己搜集资料的新颖程度；

(2)负面证据：引用反面的证据批评、否定、反驳他人的作品；

(3)操作型资讯：沿用其他研究者的研究方法、结果、参考工具等；

(4)说服：引用文献说服他人；

(5)正面评价：对于同领域的论文或相近的研究成果给予正面评价；

(6)提醒：提醒读者注意背景资料、原始资料和最新资料；

(7)社会认同：为了得到他人在学术上的认同而引用文献。

我们可将上述七类动机分成下列三组：

第一组：说服、正面评价、提醒和操作型资讯；

第二组：负面证据；

第三组：新颖性和社会认同。

其中第一、二组分别为被引文献的正面和负面的影响，但不管是正面的影响还是负面的影响，被引文献对引用文献均产生了相对重要的作用，对知识的进步起到了推动的效果。而第三组的引用只是为了使引用文献得到认同而列出被引文献，对引用文献的结果并未起到实质性的促进作用。另外，第三组出现的次数相对较少。Zhao,Zhang和Tang(2005),Teufel et al(2006)等对引用文献的内容进行分析，根据被引文献在文中被引的信息进行文本分析，根据特征词将被引文献和引用文献间的引用关系分到相应的类别中。因为鉴于涉及所有文献的全文，但在实际分析中通常只能获得文献的引文信息，全文不易获得，所以不能利用全文对不同的引用关系进行区分。退而求其次，我们将试图建立相关的指标来对不同的引用关系进行区分，对第一、二类赋以较大的权重，并对第三类引用赋以较小的权重。

在修正模型中，我们选择文献间的相似度作为区分第三组文献引用动机的指标：若被引文献对引用文献起到正面、负面的影响，文献间的相似程度相对较高；若被引文献只是起到社会认同的作用，则文献间的相似程度相对较低。即相似度越高则贡献越大，反之亦然，这与实际情况是相吻合的。因为在研究过程中，研究人员总是精读与自己研究内容最相关的文献，使得这些文章在研究过程中产生的影响也相对其他文章更加重要。在网页排序中，已经有利用网页的相似性进行排序的研究：Lin et al(2007)提出了PageSim算法，PageSim算法在PageRank算法的基础上根据网页间的相似性对网页进行重要性排序。Wang et al(2006)在PageRank算法和TFIDF算法的基础上，提出了NewPR算法，该算法综合利用网页内容和网页链接信息对网页重要进行评价。

下面介绍本文中使用的文献相似度指标—基于文献文本信息的文献相似度，此文献相似度与空间向量模型(Vector Space Model,VSM)中的相似度的概念十分相近。文献相似度是我们构造马氏链转移矩阵的重要概念。

假设文献j是文献i的被引文献，记文献i和文献j之间的相似度为sij，每篇文档都可表示为一个向量v，向量的每一维度对应文献或文献的一个关键词，总的维数为两篇文献中所有相异的关键词的个数，向量中元素的取值为相应的关键词在该文献的标题、关键词和摘要中出现的频数。这个模型假设，文献间的相关程度，可以经由比较两篇文献（向量）间的夹角偏差程度而得知。

若文献不是文献的被引文献，则令sij=0。

与网页链接相似，引文网络中有相当数量的节点没有出度，即论文后没有相应的参考文献，这种类型的论文基本表现为引文网络的根节点。产生该现象的原因有：

(1)该论文本身没有参考文献。或者是因为论文完全由作者独创，没有相关的参考文献；或者是论文不符合学术规范，没有如实列出相应的参考文献。

(2)该论文本身具有参考文献，但由于引文数据库收录范围的限制、统计分析年限的限制，使得其参考文献没能进入统计分析的范围。

我们将上述没有参考文献的文献（节点）称为悬空点，为了消除悬空点对算法稳定性的影响，我们对相似矩阵进行相应的修正：用一个n×1列向量a来标识悬空点，如果端点i是悬空点，则ai=1；否则令ai=0。令一个1×n行向量w表示访问所有端点的某个概率分布(∑wi=1)，应用最多的是均匀分布，即w=(1/n，1/n，…，1/n)。于是修正后的相似矩阵可表示为

S'=S+aw

当然，这种修正会改变原引文网络的结构，势必会影响文献影响力排序，但这种改变的影响的性质、程度还有待进一步研究。在不引起混淆的情况下，我们仍然用S表示文献的相似矩阵。

下面定义马氏链的转移矩阵，记为P，P中的元素记为pij被定义为

即将相似性矩阵根据行和进行归一化。

2.2 参考文献重要程度度量的引入及阻尼因子(Damping factor)的修正

阻尼因子是评价模型中的重要参数，它能够确保文献PageRank值的存在唯一性，并且它的取值会直接影响最终的评价结果。Bressan和Peserico(2009)研究表明：对于某些网络结构，随着阻尼因子的微小变化，前k个节点的排序可能出现所有种不同的排序结果。在这种情况下，我们根据固定的阻尼因子（d=0.85）得出的评价结果就不再具有重要的参考价值。

为了解决上述问题，Fu et al(2006)在阻尼因子的理解上另辟蹊径，对PageRank算法进行了改进。改进的PageRank算法把阻尼因子当作是一种权重，重要的文献应得到较大的权重，不重要的文献应得到较小的权重，并利用入度与相关出度的比值作为这种重要性的度量，从而避免了阻尼因子最优值的选取。但改进后的模型不再是马氏链模型，使得模型缺乏相关的理论基础，不利于进一步分析模型收敛和模型敏感度等性质。

在这一部分，我们借鉴Fu et.al(2006)对阻尼因子的理解，构造相应的转移矩阵，建立基于马氏链的文献评价修正模型。修正模型不仅避免了原有PageRank算法中选取最优阻尼因子的问题，而且能够为进一步分析提供了理论基础。

我们将阻尼因子定义为如下向量：

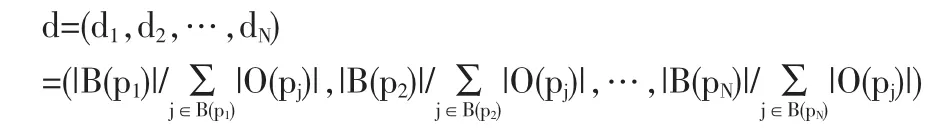
其中，di为第i篇文献所对应的阻尼因子，其含义为：在第i篇文献所影响的文献中，第i篇文献所影响的比重。影响的比重越大，则阻尼因子越大；反之，比重越小，则阻尼因子越小。

在上述阻尼因子定义的基础上，我们提出改进算法，即：利用上述阻尼因子作为权重，将相似矩阵和均匀矩阵做线性插值得随机矩阵：

其中，U是所有元素取值为1/N的N×N矩阵。

从上式可以看出，当参考文献与文章越相似，同类参考文献数越少，该参考文献被阅读的概率也越大。这一特性是与真实的文献浏览过程相一致的。

在给定转移矩阵的基础上，对应的马氏链也相应地确定，文献的PageRank值即为该马氏链的平稳分布，则文献的PageRank值可通过解下列方程得到：

其中，R是待评文献的PageRank值，τ是到任意文献的跳转概率的加权平均：

至此，基于马氏链的文献评价修正模型已成功建立，模型的求解仍然可以利用计算PageRank算法的幂法。因为同为计算矩阵的特征向量，修正模型具有与PageRank算法相同的计算复杂度。

3 总结和进一步讨论的问题

本文主要是针对基于马氏链的文献评价模型中所存在的问题，提出了基于马氏链的文献评价修正模型，是在理论模型方面所做的有益尝试。首先，修正模型创新性地在评价模型中引入了引用动机的概念，在原有引文网络的基础上考虑了文献的文本信息，根据文献间的引用关系计算马氏链的转移概率矩阵；其次，阻尼因子是根据文献的相对重要程度进行选择，不同的文献具有不同的阻尼因子，进而给出基于马氏链的文献评价修正模型。

本文只是一些初步的工作，仍有很多的问题有待解决。首先是对文献评价方法效果的检验，现有的实际应用中并没有行之有效的检验方法，也正是因为缺乏行之有效的评价方法，才使得许多优秀的评价方法引不起重视、得不到应用。在接下来的研究中我们将结合已有的研究成果(Lehmann et al,2006)，对文献评价方法的效果进行讨论，进而检验我们提出的修正模型的评价效果。

另外，随着Internet的发展，电子期刊、Working paper等形式的出现，引文结构也正在逐渐发生变化，文献间的相互引用成为可能，对传统的文献评价方法提出挑战，结合新的引文结构进行文献评价是未来文献评价的重要方向。

[1]Bressan,M.,Peserico,E.Choose the Damping,Choose the Ranking?[A].Algorithms and Models for the Web-Graph[M].Heidelberg:Springer Berlin，2009.

[2]Brooks,T.A.Evidence of Complex Citer Motivations[J].Journal of the American Society for Information Science,1986，37(1).

[3]Fu,H.H.,Lin,D.K.J.,Tsai,H.T.Damping Factor in Google Page Ranking[J].Appl.Stochastic Models Bus.Ind，2006,22.

[4]Langville,A.N.,Meyer,C.D.Google’s Page Rank and Beyond:The Science of Search Engine Rankings[M].New Jersey:Princeton University Press，2006.

[5]Lehmann,S.,Jackson,A.D.,Lautrup,B.E.Measures for Measures[J].Nature,2006,444(7122).

[6]Lin,Z.,King,I.,Lyu,M.R.Page Sim:A Novel Link-based Similarity Measure for the World Wide Web[C].Paper Presented at the Proceedings-2006 IEEE/WIC/ACM，2007.

[7]Page,L.,Brin,S.,Motwani,R.,Winograd,T.The Page Rank Citation Ranking:Bringing Order to the Web[Z].Technical Report,Stanford Digital Library Technologies Project,1998.

[8]Pinski,G.,Narin,F.Citation Influence for Journal Aggregates of Scientific Publications:Theory,with Application to the Literature of Physics[J].Information Processing and Management,1976,12(2).

[9]Teufel,S.,Siddharthan,A.,Tidhar,D.Automatic Classification of Citation Function[C].In Proceedings of EMNLP-06，2006.

[10]Wang,H.M.,Rajman,M.,Guo,Y.,Feng,B.Q.New PR-combining TFIDF with Pagerank[Z].Lecture Notes in Computer Science(Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics)(Vol.4132 LNCS-II).A-thens，2006.

[11]Zhao,P.,Zhang,M.,D.,Tang,S.Finding Hidden Semantics behind Reference Linkages:an Ontological Approach for Scientific Digital Libraries.In The Database Systems for Advanced Applications[C].10thInternational Conference,LNCS,Springer,Beijing,2005.