Bernstein多项式的移位-加算法

谷 峰

(浙江经济职业技术学院，浙江 杭州 310018)

在高级计算系统中，可以很容易地找到Bernstein多项式的算法[3]。 例如 ，在 Mathematica中 ，(t)可以用BernsteinBasis[n，i，t]计算。用高级语言编程计算 Bernstein多项式也非常容易。本文讨论如何在基本计算系统(仅具备移位、加和逻辑运算功能的计算系统)中计算Bernstein多项式。基本计算系统存在于许多系统中，例如工业控制系统、军事应用系统、医疗应用系统等。典型的有单片机系统和FPGA(Field Programmable Gate Arrays)等。

CORDIC算法是可计算多种基本初等函数的移位-加算法[4-6]。参考文献[7-8]扩展了CORDIC算法，其收敛性和误差估计在参考文献[7]中做了分析。随着硬件技术的发展，这些快速统一移位-加算法可以用硬件实现，而且不需使用乘法器[9]，成本较低，也可以用汇编语言编程实现。本文提出一个基于CORDIC算法的Bernstein多项式移位-加算法。

1 算法的描述

[7]中定义了符号函数和正规序列：

设ε为误差上界。Bernstein多项式的移位-加算法包含一个主程序和一个子程序：

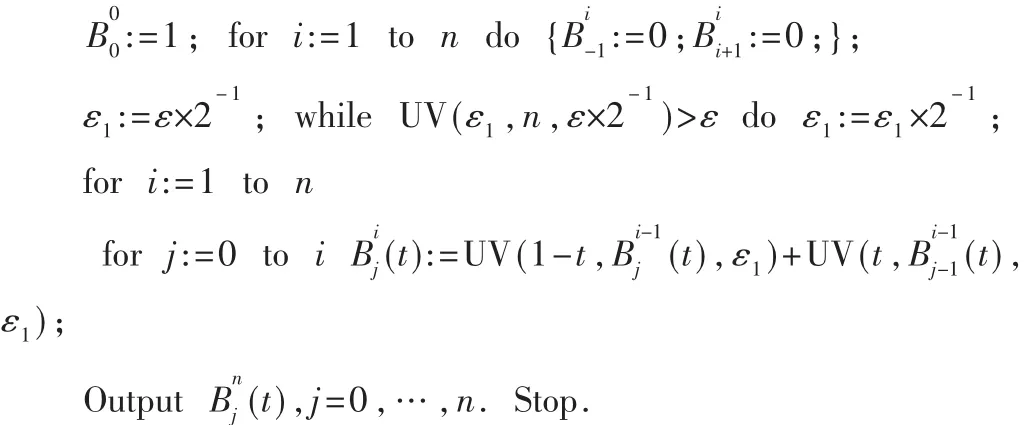
注：(1)算法中仅使用了移位运算(即 2-i×t)和加法运算。

(2)迭代次数N根据后面的定理1确定。

(4)计算实践表明子程序运行的迭代次数一般不超过28步，因此是个快速算法。

2 算法的收敛性和误差分析

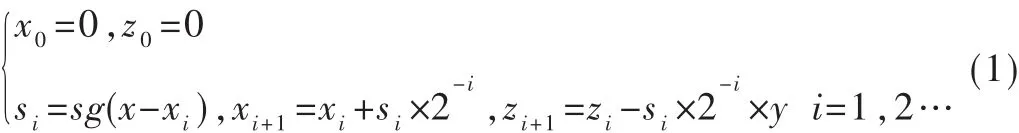
当 n充分大时，有 xn+1≈x，zn+1≈xy。

subprogram UV(u，v，ε)即基于迭代过程(1)。

(1)迭代过程(1)中的{xi}收敛于 x，且有|x-xN|≤δN-1。

(2)迭代过程(1)中的{zi}收敛于xy，且有误差估计|zN-xy|≤|y|(1+|x|)(1+δN)δN。

(3)subprogram UV(u，v，ε)中的{zi}收敛于 xy，其计算误差不大于ε。

(3)当u=0或v=0时，程序输出结果 uv=0。当uv≠0时，u 和 v 在 subprogram UV(u，v，ε)中预处理为 uv=s×2m×u1v1。 这里 s为 1 或-1。u1和 v1在(0，1]中。 由(2)，计算结果 z′N有|z′N-u1v1|＜|u1|(1+|v1|)·δN-1≤2δN-1＜δN-2；迭代次数 N 满足δN-2≤2-m×ε。 所以最终结果 zN=s×2m×z′N满足|zN-uv|＜2m×δN-2≤ε。 证毕。定理 2 主程序 Bernstein(n，t，ε)的输出值 Bn

j(t)(j=0，…，n)是n次Bernstein多项式的计算值。计算误差上界是ε。

3 数值实验

给定误差上界ε=0.000 000 5，用本文给出的算法计算三次Bernstein多项式(t)(j=0，1，2，3)的数值。 计算值见表 1。 subprogram UV(u，v，ε)中的迭代次数不大于28。三次Bernstein多项式的函数值列表如表2所示。由此可见计算误差符合要求。

参考文献

[1]NATARAJ P S V，AROUNASSALAME M.A new subdivision algorithm forthe bernstein polynomialapproach to global optimization[J].International Journal of Automation and Computing， 2007，4(4):342-352.

[2]FARIN G.Curves and surfaces for computer-aided geometric design:a practical guide， 4th Ed.Academic Press， San Diego，1997.

[3]FENG Jieqing，PENG Qunsheng.Fast algorithm for composition of the bernstein polynomials[J].Journal of Computer-Aided Design&Computer Graophics， 2001，13(2).

[4]VOLDER J E.The CORDIC computing technique[J].IRE Transactions on Electronic Computers， 1959，8(9):330-334.

[5]MULLER J M.Elementary functions，algorithms and implementation.BirkhauserBoston， 1stedition，1997.2nd edition，2006:133-156.

[6]EKLUND N.CORDIC:elementary function computation using recursive sequences [C].InternationalConference on Technology，1998.

[7]GU Feng.Convergence and error estimation of coordinate rotating algorithm and its expansion[J].Chinese Journal of Numerical Mathematics and Applications， 2006，28(2):1-9.

[8]HU Xiaobo， HARBER R， BASS S.Expanding the range of convergence of the CORDIC algorithm[J].IEEE Transactions on Computers， 1991，40(1):13-21.

[9]ANDRAKA R.A survey of CORDIC algorithms for FPGA based computers[C].In Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays(FPGA)1998:191-200.

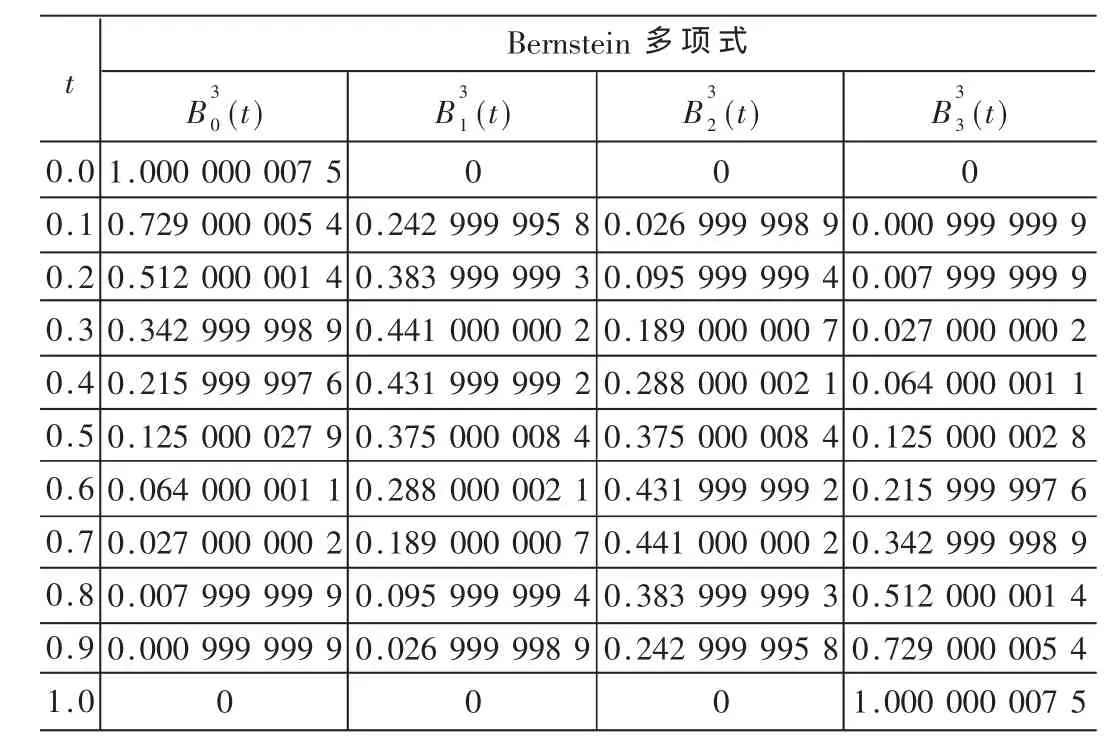
表1 三次Bernstein多项式的计算值

表2 三次Bernstein多项式的函数值