基于Markov转移模型的中国股市状态转换研究
苗 苗 ,洪 潇 ,付立新
(1.石家庄经济学院:a商学院,b经贸学院,石家庄 050031;2.中南财经政法大学,武汉 430074)
1 Markov转移模型的介绍
对于马尔科夫模型而言,每个状态都是决定性地对应于一个可观察的物理事件,所以其状态的输出是有规律的。然而,这种模型限制条件过于严格,在许多实际问题中无法应用。于是人们将这种模型加以推广,提出了马尔科夫模型(HMM)。马尔科夫过程是一种双重随机过程。即:观察事件是依存于状态的概率函数,这是在HMM中的一个基本随机过程,另一个随机过程为状态转移随机过程,但这一过程是隐藏着的,不能直接观察到,而只有通过生成观察序列的另外一个概率过程才能间接地观察到。
对于马尔科夫模型的应用,在语音识别领域已经取得了很好的成效,在信息抽取领域的应用也正在不断的尝试和推广中。
马尔科夫模型(HMM)的模型参数:
(1)N:模型状态数。
(2)M:每个状态可能输出的观察符号的数目。
(3)T:观察符号序列的长度。
(4)A={aij}:状态转移概率矩阵。
(5)B={bj(k)}:观察符号的概率分布集。
(6)π={πi}:初始状态概率分布。
一般地,由于当A、B确定后,M、N也随即确定,故通常将一个 HMM 描述为 λ(A,B,π)。
2 数据的描述性统计
2.1 数据来源及预处理
本文所采取的研究指标股价指数,数据来源于深交所,时间跨度为1998~2008年,精确到月,共计108个数据。有学者认为由于股指(Index)。
显著的“广义非平稳性”,致使它的统计特性随时间变化而呈现出不稳定性,不适宜作为研究股市的指标。笔者认为这是一种相对的概念,可能由于选取日为单位的金融序列分析较易出现非平稳的现象。为了验证月度股指数据同样适宜做股市波动研究,将在下文进行平稳性检验。
首先对数据进行预处理,相对股指stt=[(indexi/indext-1)-1]*100。得到ST序列,表示如图1。然后对相对股指序列的平稳性进行检验,由图1可知ST序列无趋势项且有常数项,所以运用 ADF-Test的(C,0,0)模式进行检验,结果如表 1。 结论显示ST序列存在单位根不平稳。但是这个结论并非常有效,ST序列图形显示只是在2007~2008年存在大幅的震荡,属于大的结构突变,在2008年底趋势回稳。

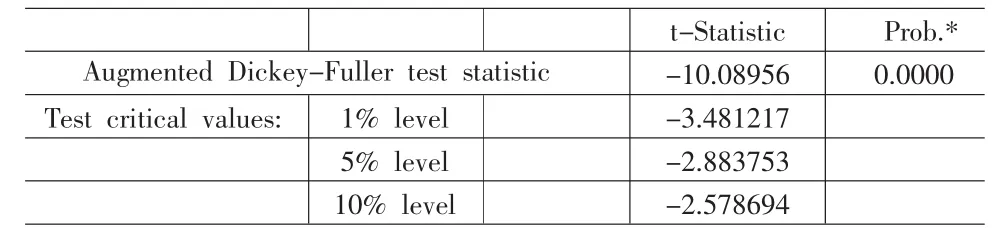
表1 数据平稳性检验
2.2 Skewness和kurtosis检验
偏度Skewness和峰度kurtosis是以正态分布为基础,分析总体数据对均值的偏离状况,具体表达式如下:


偏度Skewness的正负决定着整体分布的左右偏,绝对值大小决定偏离的幅度。同理,峰度kurtosis的正负决定着整体分布的高和矮(kurtosis≥≤3)。描述统计结果如表2。

表2 描述性统计
表2显示出深市的相对股票指数波动非常剧烈,标准差达到了19.58,偏度为7.548—明显的后尾状态,峰度83.48表现出了尖峰态。Jarque统计量为36879,显著拒绝正态分布假设。
2.3 滚动方差分析结果
图2是滚动方差的结果。具体分析方法为:以每一年的连续12个数据作方差统计,得到各年(共11个数值),其中每第一个点代表本年12个月的样本区间的方差。可以看到,1997年1月之后,中国股市的波动迅速减小。从1998年开始,绝大多数区间的方差再也没有超过10,而在1998~1999年区间,其方差大于 10,在 2006年,波动性突然增强,接近2007年由于疯牛市的存在,滚动方差飙升。大量的研究成果表明从1996年涨停板制度实施后,中国股市波动性呈收敛状态。故1998~2006年间收敛于弱式有效。如张兵、李晓明证实中国股市从1997年收敛于弱式有效。因此,1997年1月是股市波动的结构变动点。

3 实证分析及结果
3.1 相关定义
按照目前通行的观点,将股市分为熊市、疯牛市和慢牛市三种状态。股市数据的波动只是这三种状态具体的数字体现。故用数字来定义这三种状态。
S1=-1熊市,S2=1疯牛市,S3=2慢牛市
S=-1所代表的熊市含义如下:股价指数逐渐下降,体现在相对股指为负数。
S=1,所代表的疯牛市为股价指数缓慢上升,体现在相对股指为正但是非常小,本文界定为10<ST。(由于我国GDP年增长速度接近10%,故选取10为分界点)
S=2,所代表的慢牛市为股价指数急剧上升,体现在相对股指为正且比较大,本文界定为0<ST≤10。
根据上述分类标准,对ST序列进行状态分类得到状态序列Z,并且绘制状态图3(spike形式)。
从Spike图可以看出,无论熊市、疯牛市和慢牛市,都存在一个明显的聚集现象,这和众多学者采用GARCH模型所得到的:股市波动具有强的聚集性。1998~2005年,相对股指较为平稳,绝大多数时间处于慢牛市和熊市状态,只有在1999、2002、2005偶尔出现疯牛市状态。1996年和1997年在国民经济实现“软着陆”之后,证券市场已得到超前的反映,并出现过度投机的状况,1998年就是对这一过度投机进行调整的一年,并取得了重要的成绩,走出了“先扬后抑”的态势,所以导致在1998年年底至1999年期间股市疯涨,并且持续时间较长;2002年中国股市的走势是对2001年深幅下跌行情的延续,全年深股市跌幅达-18.32%,指数走势呈“M”字型,因为市场大多数人持中性预期,他们力图避开“牛熊"之争,认为A股市场将呈箱形震荡。以沪综指为例,箱顶不超过2000点,箱底不超过1300点。到2006~2007年,人民币总体上处于不断升值状态,并且利率不断降低,房价持续攀升,致使大量的流动性资金涌入股市,形成疯牛市。
3.2 股票指数的Markov过程

首先结合Markov过程来设定模型。具体包括以下:
(1)Yt——随机变量,表示在时间t时相对股指的状态,
(2)t——单位时间(年),t=0,1,2……,
(3)S——状态集合,S={s1,s2,s3},S集合中的元素为上节所确定的股市状态。
股市最后发展的状态为慢牛市最佳,能够适应经济不断发展,股市正向的合理波动与经济发展速度相对应。既疯牛市和熊市状态将消失。据此可假定贫困、疯牛市和熊市为非吸收状态,慢牛市是吸收状态,相应的可将状态矩阵划分为两大类:
T={s1,s2}——非吸收状态,
A={s3}——吸收状态。
(4)状态转移矩阵
利用Markov过程来分析相对股指的变化趋势,就是一个随时间改变的动态分析方法,用状态转移矩阵来表示各种状态每隔一年的转移情况。状态转移矩阵是利用Markov模型进行分析的关键要素,用矩阵P来表示:


表2 1998~2008年处于不同状态数

表3 2009~2015年深市股指状态数
其中pij表示在某时刻股市处于Si状态但一个单位时间后处于Sj状态的概率,同时满足以下性质:Pij≥0,并且Pij=1,i=1,2,3;j=1,2,3,根据上面对状态性质的划分可以得到:
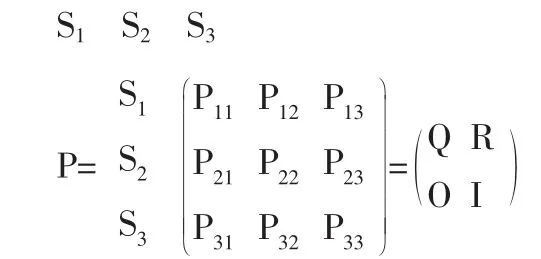
由1998~2008年的相对股指可看出,熊市状态46个月,疯牛市19个月,慢牛市66个月。下文以年为单位来确定转移矩阵,具体做法是:以相邻两年的股市状态数据作为出发点,求解转移系数,然后再将得到的10个转移系数加权平均,得到权重转移系数矩阵。首先对时间序列得出各年不同状态数目。
如1998~1999年的状态转移可以描述为:

以此类推计算出其余10个转移矩阵。

将3×3矩阵的9项数据进行平均,得到年之间股指状态的转移矩阵,具体如下:

从上述矩阵可知,当股市初始状态时熊市时,有0.24的概率向疯牛市转移,而向慢牛市转移的概率很小。充分说明了我国股票市场的波动性非常大,很少遵循正常的价值规律来运行。当初始状态为疯牛市时,向熊市和慢牛市转移的概率几率相当,并且概率仅仅为10%,说明疯牛市的惯性很大,这与我国股民的投资心理不成熟,具有显著的“羊群”效应有关。当股市初始状态为慢牛市,转移到疯牛市的概率相当的高,接近0.2。说明目前,我国股市的普遍预期还是比较高的。另外由于处于经济体制转轨的关键时期,国家出台了积极的财政政策及扩张的货币的政策来保持经济快速稳定的发展,也客观的导致了股市在国民经济中的地位逐渐攀升。
根据此转移矩阵,本文以2008年的深市股指状态为基础,对2009~2015年的股票指数进行预测。具体计算结果如下:
预测结果表示,随着金融体制的不断完善和投资者心智的不断成熟,股市波动性将会逐渐平稳:熊市一直持续在2个月左右,慢牛市持续时间呈逐渐下降态势,与其对应的疯牛市持续将以每年增加3~4天左右的时间增长。
4 总结
目前国内已经有不少学者对包括股市在内的中国资本市场进行了全方位的研究,但是都是在基于一定前提假设条件下的。很多研究结论表明:关于资本市场研究的假设条件在不断的发生变化,以致结论五花八门。自从美国芝加哥大学教授尤金·法玛在1965年发表的《股票市场的价格行为》一文中正式提出市场有效性假说 (Efficient Market Hypothesis,EMH)以来,很快就形成以均衡、线性思维、标准计量模型优化求解为主要特征的现代资本市场理论体系。统计物理和信息论对随机过程的研究发展了线性白噪声模型,其主要的特征是产生振幅无规则,时间序列不相关的无序扰动。 对短程相关的色噪声可以用线性迭加的白噪声信号来描写。例如,经济学家常用的色噪声模型是线性随机的自回归(AR)模型。分析随机运动的主要方法是相关分析,噪声运动的研究在工程和经济学中有重要的应用。所以 “均衡、线性、标准计量模型”的研究方法对现今资本市场系统的认识可能存在着局限性。
正是基于此,本文采用非线性的Markov状态转移模型,以年度为单位定义股市的三种状态,来系统分析股市在三种状态之间的变换及其规律。研究结论表明:长期趋势来看,随着资本市场与国民经济的联系性越来越强、各项金融政策的不断完善、投资者心智的不断成熟,股市状态波动将趋于平稳,熊市每年持续为2个月时间,疯牛市则以0.1个月/年的速度增长,慢牛市则以同等的速度减少。这与经济发展规律也是颇为类似的,目前我国经济发展速度预计为10%左右,与疯牛市存在时间的增长率具有高度相关性。结果表明,运用混沌的非线性状态法比传统计量方法更能较好的对股市进行分析和预测。
[1]谢赤,张太原,禹湘.证券投资基金投资行为对中国股市波动性影响研究[J].中国社会科学,2008,(3).
[2]赵昌文,杜江,杨记军.中国股市股指收益序列的结构性变点与重大事件反应——基于ICSS:MV算法的实证研究[J].第四届中国经济学年会参会论文,2005,(3).
[3]徐正国,张世英.高频金融数据“日历效应”的小波神经网络模型分析[J].数学的实践与认识,2007,(8).
[4]姚恩营,周玉国,孙国栋.国民收入的小波非参数自回归预测模型[J].计算机工程与设计,2009,(30).
[5]俞乔,程滢.我国公司红利政策与股市波动,[J].经济研究,2001,(4).
[6]周学农.机构投资者对中国股市波动性影响的实证研究[J].系统工程,2007,(12).
[7]陈平.文明分岔:经济混沌和演化经济学[M].北京:经济科学出版社.

