带漂移项分数布朗运动下的参数估计

孙 琳

(广东工业大学 应用数学学院，广州 510090)

0 引言

近年来，为了体现金融资产的长期记忆性，众多学者采用分数布朗运动来刻画金融资产的价格行为模式[1～3]。从而如何估计模型的参数成了近年来国内外学者关注的问题。文[4]和[5]对标的资产服从几何布朗运动下的参数估计进行了研究。文[6～8]对分数布朗运动模型进行了参数估计。上述研究都是在连续情况下对参数进行估计。对于离散情形的参数估计，主要有两种方法。一种是先求出连续时间样本的参数估计量，然后用离散时间样本逼近[9]；另一种方法是给出过程的离散化形式，然后求出参数估计量[10]。然而分数布朗运动既不是马氏过程也不是鞅，从而使得传统的空间状态转移模型以及卡尔曼滤波方法不能对其进行参数估计。本文拟采用极大似然方法对离散模式下带有漂移项的分数布朗运动进行参数估计，并研究估计量均方收敛性和一致收敛性。

本文采用随机游走逼近分数布朗运动，从而将传统的鞅方法应用与分数布朗运动下的参数估计。具体来说主要将做以下三方面的工作。首先采用极大似然方法，在利用随机游走逼近分数布朗运动的条件下，推到出带漂移项的分数布朗运动的参数估计量。其次，利用分数布朗运动的性质证明该估计量在一定条件下满足均方收敛和一致收敛。最后，给出数值算例，比较本文结果与已有结果，说明本文给出的估计量的精确性。

1 参数估计及一致收敛性

为了体现标的资产的长期记忆性，近年来，许多学者采用几何分数布朗运动刻画金融资产的价格变化过程，即t时刻标的资产的价格行为模式满足以下过程：

由文献[11]知在L1空间中采用黎曼求和可得该随机微分方程(1)的解可以表示为

其中，S0表示初始时刻标的资产的价格。由此估计模型(1)的参数等价于估计下面模型的参数：

从而可以容易对参数σ进行估计。不失一般性，本文假设波动率σ=1。同时，很多文献对赫斯特指数H进行了参数估计研究，所以本文着重研究漂移参数μ。即本文研究下面模型的参数估计

文献[10]给出了模型(3)的参数μ估计，本文旨在给出参数μ的另外一种形式的估计量，并研究估计量的统计性质。为了研究的需要，这里首先给出文献[12]中的引理。

引理1[12]分数布朗运动可以采用下面的随机游走逼近

其中ξi为独立同分布均值为零方差为1的随机变量，表示不超过 x 的最大整数，，且

首先，离散化模型(3)，我们有

将(4)代入(5)中即有

利用(5)，对于每一个 j∈{1，…，Nα}，每个 ξi可以表示为Yi，…，Yj与 μ 的函数。 因此我们有

其中A=(aij)=进一步我们可以得到

根据(7)和(8)，对于 j∈{1，…，Nα}，有

其中函数gj和hj依赖于aij和fij。 从而有

这里我们假设随机变量ξi满足标准正态分布N(0，1)。从而易得转移密度函数为

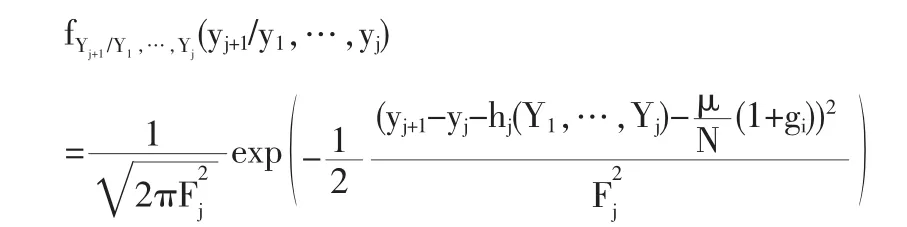
因此似然函数可以表述为

故得到参数μ的极大似然估计量为

定理1 μ的极大似然估计量(由式(10)给出)是无偏的，而且在L2空间中满足均方收敛。

证明：由式(10)，显然μ^为无偏估计量。同时由于

根据ξj的独立性，我们有

我们得到gj满足下面关系

从1到Nα-1求和我们得到

因此

从而

另一方面，我们有

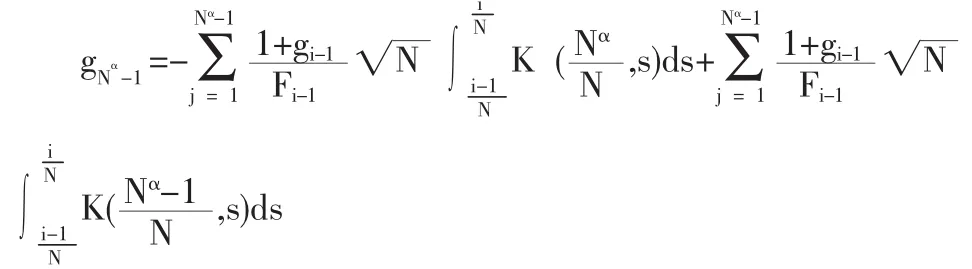
将 Nα-1改为 Nα

再由柯西不等式可得

其中C为一个正数。即

从而有 E|μ^-μ|2≤CN(2-2H)(1-α)，定理证毕。

定理2 μ的极大似然估计量(由式(9)给出)强收敛，即满足

证明：要证明(12)，利用 Borel-Cantelli定理，只需证明:存在ε使得

取0＜ε＜1-H，则由Chebyshev不等式以及Nelson's hypercontractivity不等式[13]，立即得到

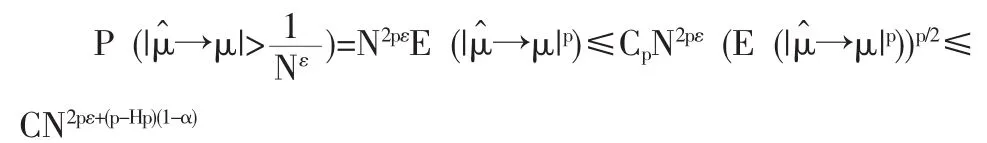
对于足够大的 p，我们有 2pε+(p-Hp)(1-α)＜-1 如果 α＞-1。从而(13)式成立，再根据Borel-Cantelli定理易得(12)式也成立，定理证毕。

2 算例

为了说明本文提出的估计量的准确性，我们对本文提出的估计量进行数值分析。首先根据文献[14]的算法产生分数布朗运动，继而得到不同的赫斯特指数下模型(3)的路径如图1、图 2。

同时，我们根据不同赫斯特指数，对比文献[10]和本文提出的估计量。对于每次模拟，设定N=200且α=1.305。然后根据估计量的表达式计算所得结果分别如表1和表2所示。其中表1给出了根据文献 [10]结果计算的估计量均值及标准差；表2给出了根据本文结果所得的估计量均值及标准差。

从表中的结果可以看出，不同赫斯特指数下漂移参数的估计均值都非常接近实际值，且方差非常小。从而可以得出只要样本容量足够大的话，方差就可能接近于零。同时可以发现在同样的前提下，本文提出的估计量比文献[10]给出的估计量更接近真实值且方差更小，说明了本文提出的估计量的优越性。

3 结论

本文对带漂移项分数布朗运动下模型进行了参数估计，并研究了估计量的收敛性，进一步用数值算例说明了本文提出的估计量的精确性。对比文献[10]和本文的估计量，可以得出以下结论：在理论方面前者提出的估计量不仅依赖于观察量Yj，同时也依赖于模拟量ξj。而本文提出的估计量仅仅依赖于观察量Yj。在数值模拟结果方面，本文提出的估计量比文献[10]的估计量具有均值更接近真实值，方差更接近于零的特点。所以本文在理论和实际应用上都有所创新。当然，如何采用更好方法得到更高阶收敛的估计量有待进一步研究。

表1 根据文献[10]计算的不同赫斯特指数下的值

表1 根据文献[10]计算的不同赫斯特指数下的值

μ的真实值μ的均值μ的方差μ的真实值μ的均值μ的方差H=0.55 0.1000 0.1019 0.1205 0.8000 0.8035 0.1013 H=0.60 0.2000 0.1960 0.6835 0.9000 0.9035 0.1962 H=0.65 0.3000 0.3078 0.1135 1.0000 1.0869 0.3073 H=0.70 0.4000 0.4035 0.1529 1.1000 1.1143 0.4025 H=0.75 0.5000 0.4912 0.1689 1.2000 1.1689 0.4926 H=0.80 0.6000 0.5931 0.1321 1.3000 1.3325 0.5907 H=0.85 0.7000 0.6891 0.1054 1.4000 1.4054 0.6973

表2 根据本文结果计算的不同赫斯特指数下的值

表2 根据本文结果计算的不同赫斯特指数下的值

μ的真实值μ的均值μ的方差μ的真实值μ的均值μ的方差H=0.55 0.1000 0.1014 0.0201 0.8000 0.7984 0.0962 H=0.60 0.2000 0.2009 0.0634 0.9000 0.9018 0.0375 H=0.65 0.3000 0.2989 0.0843 1.0000 1.0325 0.0156 H=0.70 0.4000 0.4003 0.0354 1.1000 1.0985 0.0364 H=0.75 0.5000 0.5013 0.0537 1.2000 1.2009 0.0658 H=0.80 0.6000 0.5976 0.0549 1.3000 1.2987 0.0954 H=0.85 0.7000 0.7012 0.0345 1.4000 1.4019 0.0648

[1]Hu Y,Øksendal B.Fractional White Noise Calculus and Applications to Finance[J].Infinite Dim.Anal.Quantum Probab.Related Topics,2003,(6).

[2]Wei-guo Zhang,Wei-lin Xiao,Chun-xiong He.Pricing Equity Warrants under Fractional Brownian Motion Model and Empirical Study[J].Expert Systems with Applications,2009,36(2).

[3]孙琳.分数布朗运动下带交易费用的期权定价[J].系统工程,2009,27(9).

[4]KiseÎáak J,Stehlík M.Equidistant and D-optimal Designs for Parameters of Ornstein-Uhlenbeck Process[J].Statistics and Probability Letters,2008,78.

[5]区诗德,黄敢基,杨善朝.欧式期权价值评估的非参数估计[J].系统工程,2006,24(8).

[6]Prakasa Rao,B.L.S.Identification for Linear Stochastic Systems Driven by Fractional Brownian Motion[J].Stochastic Analysis and Applications,2004,22(6).

[7]Tudor, C.A. Viens, F.Statistical Aspects of the Fractional Stochastic Calculus[J].The Annals of Statistics,2007,35(3).

[8]Hu,Y.,Nualart,D.Parameter Estimation for Fractional Ornstein-Uhlenbeck Processes[J].Statistics and Probability Letter,2009,(1).

[9]肖庆宪.Ornstein-Uhlenbeck过程的参数估计[J].应用概率统计,2005,21(1).

[10]Bertin,K.,Torres,S.Tudor,C.A.Maximum Likelihood Estimators and Random Walks in Long Memory Models[J].Statistics and Probability Letter,2009,(11).

[11]Kallianpur,G.,Kallianpur,R.L.Introduction to Option Pricing Theory[M].Boston:Birkhäuser，1999.

[12]Sottinen,T.Fractional Brownian Motion,Random Walks and Binary Market Models[J].Finance and Stochastics,2001,(5).

[13]Hu,Y.A Unified Approach to Several Inequalities for Gaussian and Diffusion Measures.Séminaire de Probabilités[J].XXXIV,Lecture Notes in Math,2000.

[14]Paxson,V.Fast,Approximate Synthesis of Fractional Gaussian Noise for Generating Self-Similar Network Traffic[J].Computer Communications Review,1997，27.