视频网格中流媒体业务的流量模型

高伟涛,崔占忠,张海旸

(1.北京理工大学 宇航学院, 北京 100081； 2.北京邮电大学 计算机科学与技术学院, 北京 100876)

网格是目前比较热门的一个研究领域,它被普遍认为是下一代的互联网. 网格最大的特点是各种资源的充分共享,这种共享是智能的、普遍的和便利的,这使得网络上的各种资源可以得到充分有效的利用,并且精简了网络终端的功能. 在网格中较为普遍的一种服务就是VoD服务,因此针对多媒体服务中的视频流进行研究，可以为这种多媒体服务提供更好的QOS保证.

在网格中服务的方式采用多对多服务模式,也就是多个服务器对多个用户进行并行服务. 这样可以充分、有效地利用这多个服务器的资源,并且可以为用户提供更稳定、优良的服务质量. 在这种服务模式下,Internet网络的多媒体VoD的视频流模型已经不再适用,为此作者在已有VoD视频流模型的基础上，提出了三层随机过程描述方式,对网格中的VoD服务中的视频流进行建模.

较早的视频业务流量模型是由Maglaric等人提出的一阶自回归AR模型[1],在此基础上R.Grunenfelder和徐树公等分别提出了ARMA模型及基于Gamma分布的AR模型[2-3]. 这些模型将视频数据流量视为一个平稳随机过程,只适合于无场景变化的视频源. 而实际的视频流大多是非平稳随机过程,文献[4-5]中根据I帧或GOP的数据量大小,通过阈值分割法,将这一非平稳随机过程划分为一段段近似平稳随机过程,但是这种分割方法的阈值不易确定. 文献[6]中提出了基于视频图像内容的分割方法,提出了由AR模型调制的半马尔可夫随机过程,它可以适合于各种场景的视频业务流量模型.

作者针对网格中不同的流媒体服务方式,对AR模型进行了改进,提出了复合AR模型(MAR). 在视频图像分割方法的基础上,将一段视频分割成为多个视频片断,把每一个视频流片断内部当作平稳过程看待,采用AR模型来描述,把每一个视频流片段之间近似看作是半马尔可夫过程. 并且考虑到了不同视频流段的来源不同，从而仅在每一个视频流段中视频流片断符合半马尔可夫过程,而在整个视频流中各个视频流片断符合泊松分布.

1 网格中的VoD服务模式

在网格中有多个VoD服务器对用户同时提供服务，在此只考虑一个用户情况下的服务模式,将多对多模型简化成为多对一的服务模型. 不失一般性,假设有3个VoD服务器,通过3条不同带宽、不同延迟和不同丢包率的链路来同时为一个用户提供服务. 这3个服务器分别为S1,S2,S3,3个链路的带宽分别为B1,B2,B3,3个链路的延迟分别为τ1,τ2,τ3,3个链路的丢包率分别为ε1,ε2,ε3. 网格中的VoD的多对一的服务种类有2种：一为多个VoD服务器,每个根据自身的带宽、延迟和丢包率分别传输一段视频流给用户,在客户端将这些视频流进行合成；二为从这些VoD服务器中选择一个性能最优的服务器来为用户提供服务,在其它的服务器中选择一个备份服务器组提供各种备份流以保证不同的服务质量要求.

本文中讨论多个VoD服务器，每个服务器根据自身的带宽、延迟和丢包率的合成函数,分别传输一段视频流V1,V2,V3,在客户端将这些视频流段进行合成. 每个视频流段的时间长度用式(1)计算

t=C1B+C2τ+C3ε.

(1)

式中C1,C2,C3分别为带宽、延迟和丢包率在计算视频流段时间长度时的权值. 带宽、延迟和丢包率分别为归一化值,折合为时间量. 在VoD点播中,带宽为主要因素,带宽直接决定可用的传输速率. 延迟和丢包率对于VoD业务的质量、传输速率有较小的影响,对视频流的抖动有一定影响,因此C1的值应该比C2,C3大一些,其确切值由实际VoD服务进行测定.

2 网格中的MAR流媒体服务模型

假设各个VoD服务器和客户端之间的链路是稳定的,不会发生故障,链路的带宽、延迟和丢包率也是恒定的不随时间改变的,因而各个VoD服务器提供的视频流段长度固定且不随时间变化.

在VoD视频流中,当量化尺度及GOP格式固定后,其输出的数据比特流的大小主要由视频图像纹理的复杂度和图像运动的复杂度决定. 因此可以根据图像复杂度将视频流分割成一段段近似平稳的视频片断. 为简化起见,将视频片断分为高、中、低复杂度3种类型(H,M,L). 在视频片断内部,数据流可以假设为平稳的,因此可以用一阶自回归AR模型进行模拟[6]. 对于MPEG压缩方式的VoD视频流,假设GOP格式为IBBPBBPBBPBB,因此可用3个一阶AR模型分别对I，P和B帧进行模拟. 则一个视频片断可定义为[2-3]

X(i)=[ARIARPARBt(i)].

(2)

式中t(i)为每个视频段持续的时间. AR模型定义为

λ(k)=aλ(k-1)+bw(k),|a|<1.

(3)

式中：λ(k)为压缩后第k帧每个像素的平均比特数；a,b为常数；w(k)为均值为η,方差为1的正态高斯白噪声.λ(k)的均值、方差和自相关函数分别为

E(λ)=bη/(1-a),

(4)

(5)

(6)

每个来自于某个VoD服务器的视频流段由若干个视频片断组成,每一个视频片断分别属于{H,M,L}这3个状态,并且更新间距为：t={τn,n=0,1,2,…}. 令随机序列X={Xn,n≥0}具有状态空间为视频片断复杂度于视频片断来源的组合：{H1,H2,H3,M1,M2,M3,L1,L2,L3},下标1,2,3分别代表来自不同的VoD视频服务器. 对于确定的一个视频流片断,它只能在{H,M,L}3个状态之间进行转换,由于这3个状态之间的相关性与实际的视频流的内容有关,因此只能根据统计来确定这些状态之间的转移概率矩阵Pij,i,j∈{H,M,L}.

由于在每个视频片断的转移与前面的视频片断的状态无关,因此可以将随机序列X看做是马尔可夫链. 而在一个视频流段内部的视频流片断序列定义为随机过程

B={Bt,t≥0,且Bt=Xn,当τn-1≤t≤τn}.

(7)

随机过程B即为由马尔可夫链调制的半马尔可夫过程.

对于每一个VoD服务器提供的视频流来说,虽然每个视频流段的时间长度不同,但是这个长度是相对固定的. 因此可以把整个视频流看作是这些视频流段组成的Poisson过程. 来自3个VoD服务器的视频流的长度固定为Tv1,Tv2,Tv3,而且假设视频流的顺序为任意的,即V1,V2,V3,可以随机排列. 每两个视频流之间的间隔为tSi. 这样,当把视频流段的长度和间隔看成是对于视频流段到达的随机时间,则整个视频流所包含的视频流段数{N(t),t≥0}可以看成是一个Poisson过程.

(8)

λ=E{N(t)}/t.

(9)

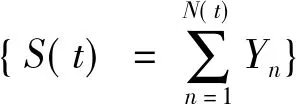
E{S(t)}=(λt)E{Yn},

(10)

(11)

而考虑到视频流片断之间是半马尔可夫过程，以及视频流片断内部是平稳随机过程,则整个视频流可以表示为三重的随机过程：在最高层,视频流可以看作由视频流段组成的类似复合泊松过程,而每个视频流段可以看成由视频流片断组成的半马尔可夫过程,最后,每个视频流片断的内部可以看成是平稳过程.

3 仿真实验

由于网格规模庞大,要在网格上实现较好的流媒体服务,对流媒体调度算法的要求非常高,在调度算法的研究中,无法直接应用到大规模的实际网格中检验其性能,必须通过仿真大规模网格,以及其上的流媒体业务模型来验证调度算法的性能.

在流媒体调度算法的实验中,对于流媒体的模型要求很高,需要更贴近实际的流媒体业务模型,以便更好地仿真出调度算法的性能,因此流媒体业务模型对于流媒体调度算法的研究意义非常重大. 在本文中,作者将在仿真环境中利用ARMA模型和本文提出的MAR模型对同一调度算法的性能进行验证,并且在小规模的网格中实现该流媒体调度算法对两种模型进行评估,从而比较两种模型与实际网格流媒体业务特征的吻合程度.

在仿真环境中使用GT-ITM生成Transit-Stub型网络拓扑,网络节点规模分别为20，40，60个节点. 主干Transit网络采用1Gbit或10Gbit网络,Transit网络与Stub之间的链路采用100Mbit网络,Stub内的各节点之间主要为100Mbit链路.

在实际网格中采用了60台PC机,配置从CPU：P43.0GHz,内存：1GB,硬盘：200GB,到双CPU：P43.2GHz,内存：2GB. 整个网络由3台路由器将3个局域网连接起来,每个局域网中有20台PC机. 并采用Globus Toolkit3.2搭建网格平台.

在仿真实验中借用无缝切换 (seamless switch, SL-Switch)[11]算法来比较采用不同流媒体模型，使得切换算法的性能与实际网络中性能的相似程度. 在SL-Switch算法中,将Buffer尺寸设为8min,并且将节点平均故障时间设为1000s,然后通过视频流的接收帧的稳定性来评估算法的性能,并且通过在ARMA模型和MAR模型下与实际网络中的稳定性差来评估流媒体模型与实际的相似程度.

图1为ARMA, MAR模型与实际网络中流媒体稳定度的比较图. 从图1中可以看出,ARMA模型与实际网格中的平均稳定性差较大,为0.15,而MAR模型与实际网络中的平均稳定性差较小，为0.90. 因而可以得出,在小规模网格中,对于多对一的流媒体服务模式，MAR模型比ARMA模型更接近于实际的流媒体业务特征.

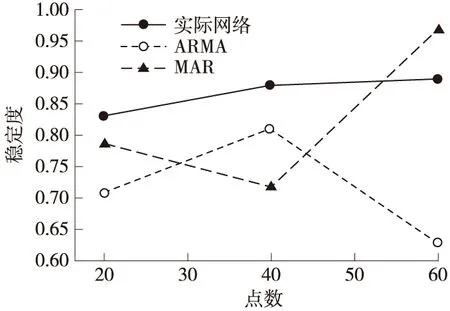
图1 ARMA，MAR模型与实际网络中流媒体稳定度的比较

4 结 论

提出的针对网格环境中多对一VoD服务中视频流的多层模型,在考虑了面向内容的多源视频流分割和多源相关性后,提出了第1层为AR模型的平稳随机过程，第2层为半马尔可夫过程，第3层为泊松过程的三重随机过程模型. 将ARMA，MAR模型与网络中流媒体的稳定性进行比较，结果表明，该模型可在网格环境下更准确有效地描述网格环境下多对一VoD服务中的视频流,为更有效和更高质量地提供VoD服务打下了基础.

参考文献：

[1]Maglaris B. Performance models of statistical multiplexing in packet video communication[J]. IEEE Trans on Comm,1988,36(7):834-843.

[2]Grunenfelder R. Characterization of video codes as autoregressive moving average process and related queuing system performance[J]. IEEE JSAC,1989,7:752-760.

[3]徐树公,黄载禄.一种新的ATM网VBR视频业务模型[J].电子学报,1997,25(10):102-105.

Xu Shugong, Huang Zailu. A sort of new ATM net VBR video frequency operation model[J]. Electronics Transaction,1997,25(10):102-105. (in Chinese)

[4]Manzoni P. Workload models of VBR video traffic and their use in resource allocation policies[J]. IEEE/ACM Trans on Networking,1999,7(3):387-397.

[5]Jelenkocvic P R. The effect of multiple time scales and subexponentiality in MPEG video streams on queueing behavior[J]. IEEE JSAC,1997,15(6):1052-1071.

[6]陆大金.随机过程及其应用[M].北京：清华大学出版社,1986．

Lu Dajin. Stochastic process and application[M]. Beijing: Tsinghua University Press,1986. (in Chinese)

[7]王玉孝.概率论与随机过程[M].北京：北京邮电大学出版社,2000．

Wang Yuxiao. Probability theory & stochastic process[M]. Beijing: Beijing University of Posts and Telecommunications Press,2000. (in Chinese)

[8]Calvert K L, Doar M B, Zegura E, Modeling internet topology[J]. IEEE Communications Magazine,1997,35(6):160-162．

[9]Sun Xiaoyan, Wu Feng, Li Shipeng. Seamless switching of scalable video bitstreams for efficient streaming[J]. IEEE Trans on Multimedia,2004,6(2):291-303．