典型玻璃材料冲击力学性能研究

安二峰,李磊,杨军

(北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)

玻璃作为一种透明的类陶瓷材料,只是与陶瓷烧制温度不同,主要成份相同,越来越得到军事科技工作者的青睐. 国内目前对该方面还未开展研究. 近年来,美国学者已开始加强玻璃材料的冲击力学性能研究,Sun Xin, Liu Wenning和Xu Nie, Weinong W. Chen等运用SHPB加载技术对军用玻璃材料进行冲击加载实验,并利用连续介质损伤力学方法、含损伤本构关系结合有限元方法对该实验进行了数值模拟[1-5]；M. Grujicic， B. Panduranga和T.J. Holmquist, G.R. Johnson等用弹丸对玻璃材料进行了冲击实验,并从细观层次对损伤演化规律进行描述,在考虑应变率效应的基础上,运用有限元方法对该问题进行了数值模拟[6-7]；B. Paliwal, K. T. Ramesh研究了脆性材料在压缩条件下,微裂纹之间的相互作用[8]；S. Chocron和K.A. Dannemann等分别研究了含初始损伤和不含初始损伤的玻璃在约束条件下力学性能及本构关系[9].

作者对类陶瓷材料(浮法玻璃和钢化玻璃)的冲击力学性能进行了研究,结合典型建筑玻璃的冲击力学性能,对类陶瓷材料的冲击破坏过程的实时监测的可行性问题进行了探讨.

1 浮法玻璃的冲击力学性能

浮法玻璃作为一种常见的建筑和装饰材料,其弹性模量和密度具有确定性；由于样品之间内部初始损伤的差别较大,其破坏强度往往具有不确定性. 目前广泛应用的冲击加载装置是由H.Kolsky于1949年提出的分离式Hopkinson压杆装置(如图1所示). 它可以对试件施加应变率为101～104s-1的冲击载荷,通过测量入射杆和透射杆上的应力波,利用间接的方法得到夹在两根压杆之间试件的动态应力、应变、应变率及其他动力学参数,有效避开了冲击作用下直接测量的困难和不可靠性. 本次实验所用压杆直径为50mm,子弹长400mm.

图1 分离式Hopkinson压杆装置示意图

对直径为32mm,厚度为15mm的浮法玻璃试件进行冲击加载,实验共进行9次；典型实验波形如图2所示,其弹丸冲击速度为7.5m/s. 对浮法玻璃的原始冲击波形进行处理,可得如图3所示的应力-应变曲线,如图4和图5所示的应力-时间曲线以及应变-时间曲线.

图2 浮法玻璃原始波形

图3 应力-应变关系曲线

图4 应力-时间曲线

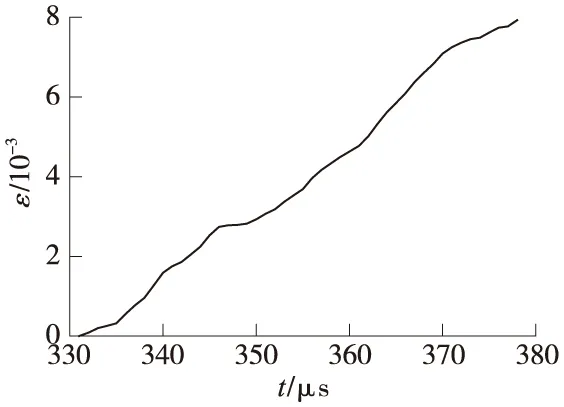
图5 应变-时间曲线

从图4可以看出：在前20μs内(330～350μs),由于加载速率急剧变化的影响,应力和应变随时间的变化不呈线性关系；在350～365μs内,基本呈线性关系；之后,随着损伤演化的发展,线性关系被打破. 该现象从图4中看得更清楚一些.

2 连续介质损伤力学模型

对于脆性材料,用连续介质损伤及其本构理论来描述脆性材料的宏观响应已成为破坏力学发展的主流. 对于冲击条件下的玻璃来说,常用经典的连续介质损伤力学模型来描述其宏观力学响应[3].

2.1 损伤演化规律

根据连续介质损伤力学模型,当拉伸主应力σi大于门槛值σth时,损伤的演化与拉伸主应力呈简单线性关系(拉应力为正),该演化方程为

(1)

式中：σi为主应力分量；Dii为损伤变量；σth为应力门槛值；σcr为应力临界值.

Sun Xin， Liu Wenning等认为,损伤的演化与最大切应力τmax紧密相关；并在式(1)的基础上,得到损伤演化方程(拉应力为正)为

(2)

式中：τth为切应力门槛值；τcr为剪切强度.

2.2 本构方程

对于浮法玻璃来说,内部物理性能表现为各向同性且无预应力,其力学性能的非线性由本构关系中的损伤变量来控制. 该含损伤本构关系可写为

(3)

(4)

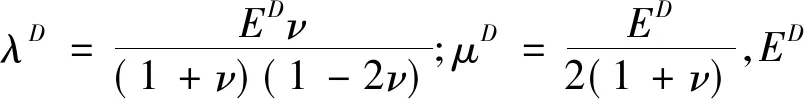
ED=E-D(E-E*).

(5)

式中：ED为损伤材料的弹性模量；E为未损伤材料的弹性模量；E*为完全破坏时的弹性模量.

3 钢化玻璃的冲击力学性能

钢化玻璃和浮法玻璃作为类陶瓷材料,两者之间具有同源性,钢化玻璃是由浮法玻璃淬冷而形成. 钢化玻璃形成后,内部产生预应力,表面呈压应力状态,内部为拉应力状态，在冲击力学性能方面比浮法玻璃更具有显著特点. 下面通过SHPB冲击加载,在与浮法玻璃具有相同试件尺寸和加载装置情况下,对其冲击力学性能进行研究.

该冲击实验针对钢化程度为半钢化的玻璃试件,共进行冲击实验12次,取得典型实验波形如图6所示,其弹丸冲击速度为v=8.82m/s. 对图6所示的原始冲击波形进行处理,可得如图7所示的应力-应变曲线.

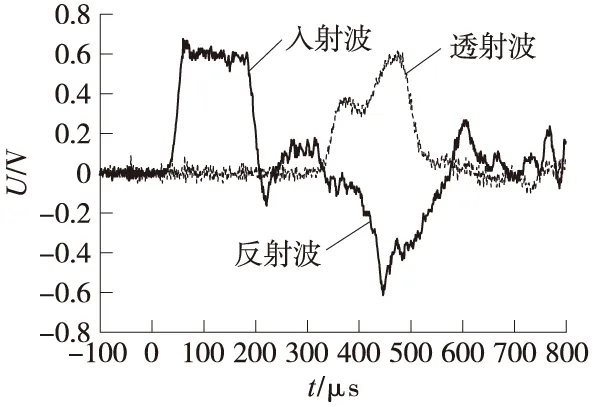
图6 钢化玻璃原始波形

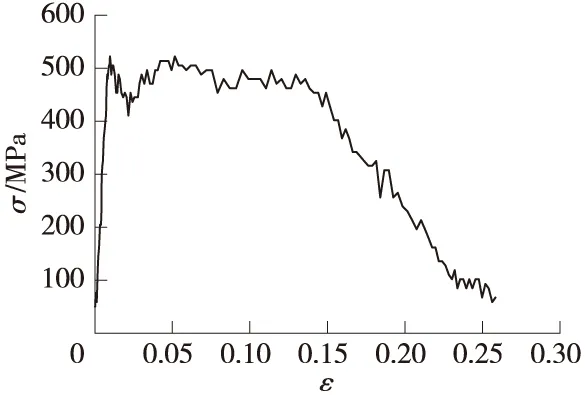
图7 应力-应变曲线

4 实验结果分析

4.1 浮法玻璃实验结果分析

对于式(2)所示损伤演化方程来说,τth和τcr都与最大主应力有关；因此,它们的取值可以直接从SHPB实验结果反映出来. 对图3的应力-应变曲线来说,由于从点A损伤开始发展,弹性模量开始降低；因此,点A应力对应τth门槛应力. 同样,到达点B处,材料发生破坏,其对应玻璃的剪切强度τcr；但τcr在应力-应变曲线上的表达比较模糊,从断裂理论来讲,最大应力并不对应其剪切强度τcr. 从图4的应力-时间曲线来看,其对应τth和τcr的确定更清晰、准确一些,但τcr的确定依然缺乏理论依据.

由于玻璃具有透明特性,玻璃裂纹表面对透射光具有高反射性；因此,在暗室进行SHPB冲击实验的同时,利用连续闪光光学高速摄影对该冲击破裂过程进行同步拍摄；但从应力-时间曲线可以看出,整个损伤破裂过程仅持续20～30μs；因此,要求高速摄影的幅频至少应在20万帧/s以上. 将高速摄影和SHPB实验得到的应力-时间曲线进行对照,对于确定τth和τcr具有更直观意义[3]. 由于浮法玻璃是一种类陶瓷材料,该研究对陶瓷材料同样具有重要意义.

4.2 钢化玻璃实验结果及对比分析

由图7所示的应力-应变曲线可以看出,钢化玻璃在冲击情况下,一开始其应力-应变关系表现为弹性,但随着压力的升高,在500MPa附近出现类金属性质的屈服平台. 初步分析认为：屈服平台的长度与钢化玻璃的钢化度和冲击速度有密切关系,该塑性屈服是一种伪塑性屈服现象,是该种材料本身的强化与微裂纹损伤增长有关的预应力释放共同作用的结果,与其破裂的物理机制有密切关系,更与金属材料的塑性屈服机制有本质区别,有待进一步深入研究. 另外,关于其弹、塑性损伤演化规律和本构关系,也不能应用式(2)(3)所示损伤演化方程和本构关系来进行简单描述,更有待深入研究.

图8 钢化玻璃的临界破坏情况

钢化玻璃在冲击条件下的临界破坏情况如图8所示,正面破坏裂纹由中间向四周呈辐射状扩展,而背面裂纹在离边界3～4mm处形成一裂纹环. 该现象的产生主要是由一维应力波弥散和钢化玻璃的预应力状态所决定.

钢化和浮法玻璃的强破坏情况如图9和图10所示,钢化玻璃的破坏呈颗粒状,而浮法玻璃的破坏呈细粉状. 可见,淬冷钢化产生的预应力分布对材料的冲击破裂形态具有显著影响.

图9 钢化玻璃的冲击破碎

图10 浮法玻璃的冲击破碎

5 结 论

运用SHPB实验装置并结合典型脆性材料损伤演化规律和含损伤本构关系及有关玻璃物理特性,探讨了浮法和钢化玻璃的冲击力学性能及其冲击过程的光学可测性. 通过以上研究,可得出以下结论.

① 浮法玻璃的SHPB冲击实验结果显示：其冲击力学性能与典型脆性材料(陶瓷等)基本一致；因此,其冲击损伤演化过程可以用式(2)(3)所示典型脆性材料的损伤演化方程和含损伤弹性本构关系来描述,有效性有待数值模拟的进一步验证.

② 损伤演化方程中τth和τcr可以通过应力-应变曲线和应力-时间曲线来确定,但τcr的确定具有一定主观性,运用闪光高速摄影和SHPB冲击实验相结合,可使τcr的确定更直观.

③ 钢化玻璃和浮法玻璃虽具有同源性,但由于淬冷而形成预应力的存在,使其冲击力学性能具有显著差异；钢化玻璃除表现出传统脆性材料的弹性性能外,还进一步表现出金属材料的塑性屈服特性.

④ 在冲击条件下,钢化玻璃和浮法玻璃的破碎形态有很大差异,钢化玻璃破碎呈颗粒状,而浮法玻璃呈细粉状. 钢化玻璃在临界冲击破坏下,正面与背面裂纹形态有很大差异,正面为辐射状裂纹,背面距边界3～4mm处有环状裂纹产生.

参考文献：

[1]Knight C G, Swain M V, Chaudhri M M. Impact of small steel spheres on glass surfaces[J]. J Mater Sci,1977,12:1573-1586．

[2]Chaudhri M M, Kurkjian C R. Impact of small steel spheres on the surfaces of “normal” and “anomalous” glasses[J]. J Am Ceram Soc,1986,69(5):404-410．

[3]Sun Xin, Liu Wenning. Modeling and characterization of dynamic failure of borosilicate glass under compression/ shear loading[J]. International Journal of Impact Engineering,2009,36(2):226-234．

[4]Xu Nie, Weinong W Chen. Dynamic failure of borosilicate glass under compression/shear loading experiments[J]. J AM Ceram Soc,2007,90(8):2556-2562.

[5]Xu Nie, Weinong W Chen. Rate and surface treatment effect on the strength of boro-glass[C]∥Proceedings of11th International Congress and Exhibition on Experimental and Applied Mechanics. Orlando, USA: SEM,2008:122-124．

[6]Grujicic M, Pandurangan B. An improved mechanical material model for ballistic soda-lime glass[J]. Journal of Materials Engineering and Performance,2009,10(S1):1665-1672.

[7]Holmquist T J, Johnson G R. Response of silicon carbide to high velocity impact[J]. J Appl Phys,2002,91(9):5858-5866．

[8]Paliwal B, Ramesh K T. An interacting micro-crack damage model for failure of brittle materials under compression[J]. Journal of Mechanics and Physics,2008,56:896-923.

[9]Chocron S, Dannemann K A, Walker J D, et al. Constitutive model for damaged borosilicate glass under confinement[J]. J Am Ceram Soc,2007,90(8):2549-2555．