液压变压器变压比特性研究

胡纪滨,李小金,魏超

(北京理工大学 车辆传动国家重点实验室, 北京 100081)

恒压网络系统是近年来发展起来的新型静液传动技术,其组成类似于电力传输系统，液压变压器则是其中关键的压力变换元件[1]. 图1为斜轴式液压变压器的结构示意图[2]. 它的配流盘上有3个相同大小的槽口,这3个槽口(A，T，B)分别与恒压网络的高压油路、低压油路和负载油路相连. 液压变压器最终输出的负载压力特性是其最为关键的特性之一. 通常这一特性表示为液压变压器的变压比,定义为液压变压器B口压力与A口压力之比. P.A.J.Achten给出了忽略摩擦和泄漏损失,不计T口压力的条件下的液压变压器理想变压比模型[3-4]. 欧阳小平则给出了假定能量损失为常数时的变压比模型[5-6].

图1 液压变压器示意图[2]

然而实际使用过程中,摩擦和泄漏损失不仅存在而且随缸体转速变化很大,导致前人建立的模型与试验结果之间存在偏差. 如图2中所示,在负载流量为10L/min时,Achten的理想变压比模型与试验结果偏离较大；采用欧阳小平的模型并取能量损失为0.5kW计算时,计算值与试验值比较接近. 当流量增大为40L/min后，两个模型的计算结果均与试验值的变化趋势明显相反. 因此有必要对液压变压器的摩擦、泄漏特性做进一步的研究,建立一个精确的变压比模型.

图2 两种模型计算值与试验值的对比

1 模型建立

图3为液压变压器的配流盘示意图,图中αA，αT，αB分别为A，T，B口的包角,一般配流盘上的3个槽口大小相等且相邻槽口之间均为0遮盖,因此可得：αA=αT=αB=120°；φX1,φX2(X=A，T，B)分别为X口包角相对于下死点的起始角度与终止角度；δ为A口中心线与下死点的夹角,称为配流盘的控制角.

图3 配流盘示意图

理想变压比公式是在忽略摩擦与泄漏损失的条件下,由缸体转矩平衡方程推导得出的. 当考虑缸体转动过程中的摩擦损失时,缸体的转矩平衡方程应写为

ΔT=pAVA+pTVT+pBVB.

(1)

式中：ΔT为摩擦损失；pX(X=A,T,B)为液压变压器X口的压力；VX(X=A,T,B)为液压变压器X口的排量，当油液流入液压变压器时为正值,流出时为负值.

排量仅仅表述槽口流入、流出流量的净差值,而无论是在吸油还是在排油过程中均有摩擦损失产生. 参考液压泵/马达的建模理论,可将摩擦损失表示为与压力成比例的机械摩擦损失以及与黏度和转速成比例的黏性摩擦损失之和，即

ΔT=CfpV+CvμωV.

(2)

式中：Cf为机械摩擦损失系数；Cv为黏性摩擦损失系数；μ为油液的动力黏度；ω为缸体转速；V为槽口流入排量或流出排量. 当配流盘转动时,各槽口的位置发生变化,相应排量也会随之变化.

当A口位于下死点时,理想变压比为0[3],此时配流盘控制角δ有最小值δmin=0；当B口位于下死点时,理想变压比为无穷大,此时δ有最大值δmax=(αA+αB)/2. 由此可得出各槽口位置相对于下死点的变化范围为

(3)

当A口位于图3所示位置,液压变压器向B口输出流量时,缸体逆时针旋转. 由斜轴式柱塞元件的工作原理可知：若以下死点为极轴,在[φA1,0]范围内,油液流出A口,流出排量为

VA,out=K[cos(0)-cos(φA1)],

(4)

式中K为与变压器结构相关的常数,对于斜轴式液压变压器K=zARtan[β/(2π)],其中：z为柱塞个数；A为柱塞面积；R为柱塞分布圆半径；β为斜轴倾角.

而在[0,φA2]范围内,油液流入A口,流入排量为

VA,in=K[cos(0)-cos(φA2)].

(5)

其中流入及流出排量均恒为非负值.

考虑整个配流盘控制角范围内A口可能处于的位置,可进一步得到：

(6)

同理,T口和B口的相应排量可表示为

(7)

(8)

将式(6)～(8)代入式(1)(2),可得

(9)

式(9)中,缸体转速实际是由液压变压器的负载流量决定的. 若进一步假设：液压变压器的泄漏为层流，忽略油液流经管路产生的压降，忽略流量的脉动. 根据流量连续定理,并考虑到流动的方向,负载流量qVL可表示为

(10)

式中Cs为层流泄漏系数.

将式(10)代入式(9)并忽略T口压力,整理后可得变压比Π的表达式

(11)

式(11)即为以液压变压器控制角度δ和负载流量qVL为自变量的液压变压器变压比模型,模型中的3个损失系数Cf，Cv，Cs可以利用试验数据回归求得.

2 结果分析与讨论

为了获取损失系数和验证数学模型,作者制造了液压变压器的原型机并进行了一系列试验. 试验所用的液压变压器由斜轴式柱塞泵改装而成. 柱塞泵的理论排量为23mL/r,额定工作压力35MPa. 柱塞泵的配流盘和后端盖被更换为具有3个相同槽口的配流盘和带有3个接口(A，T，B口)的后端盖. 通过与配流盘相连的转动轴可以旋转配流盘. 试验时A口压力为10.0MPa，T口压力为0.5MPa，配流盘控制角度为20°～100°,缸体最高转速为4000r/min.

图4给出了利用式(11)得出的计算结果. 计算时各参数取值为：Cf=5.46×10-2，Cv=1.33×105，Cs=2.59×10-8，μ=0.04Pa·s. 可以看出,本文中提出的液压变压器变压比数学模型可以很好地描述试验结果.

图4 本文模型计算结果与试验结果的比较

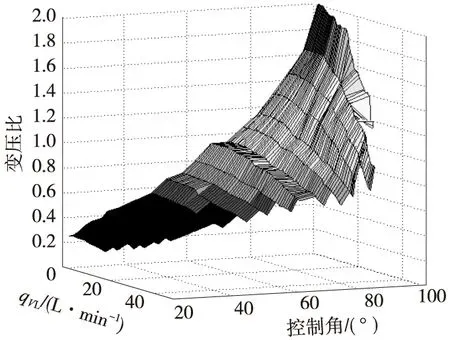
图5 变压比的试验Map图

图5显示了整个试验范围内测得的变压比Map图. 图6为同样条件下计算得到的结果. 可见,数学模型在整个工作范围内都可以较好地描述液压变压器的变压比特性. 只是在大流量、大控制角的工况时由于紊流等因素的影响造成了试验数据与理论曲线的偏差稍大. 而在配流盘控制角小于90°,负载流量小于35L/min的绝大部分范围内，本文中建立的数学模型的误差不超过14%.

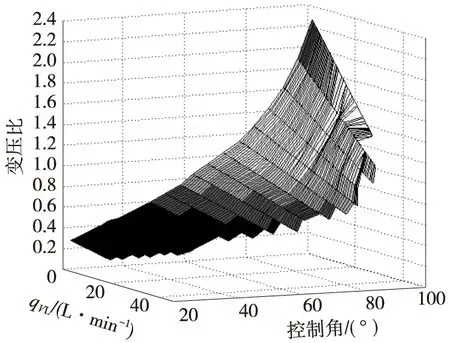
图6 变压比的计算Map图

图7所示为控制角为20°，60°和100°时的变压比-负载流量曲线. 从图7中可以看出,当控制角为常数时,变压比随负载流量的增加单调减小,并且控制角越大,变压比递减的趋势越剧烈. 在大流量、大控制角工况时，由于紊流的影响造成了试验数据与理论曲线的偏差. 可见负载流量的变化对液压变压器的变压比特性影响很大.

图7 控制角恒定时的变压比-负载流量曲线

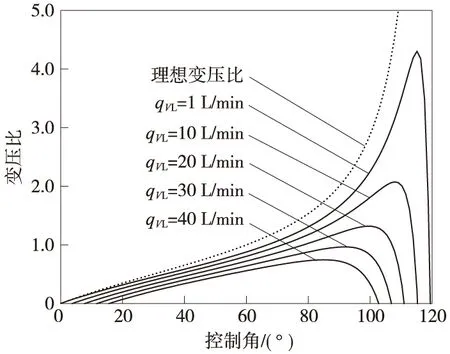
图8 不同负载流量时的变压比曲线

图8进一步给出了不同负载流量时的变压比曲线. 从图中可以看出,随着负载流量增大,变压比越来越低于理想变压比. 值得注意的是,当负载流量为常数时,由于各种损失的影响,变压比不再像理想变压比曲线一样随着控制角无限制地单调递增,而是在某一个控制角时达到一个有限的极大值，随后下降. 而且负载流量越大,可以达到的最大变压比越小,与之对应的控制角也越小. 可见在不同负载流量下,液压变压器存在不同的最大变压比和最大有效控制角,进而确定了此时液压变压器可传递的最大功率.

图9所示为液压变压器最大变压比、最大有效控制角及最大功率随负载流量的变化曲线. 由图中可以看出，随着负载流量的增大,液压变压器的最大变压比逐渐减小,而且小流量时减小速度很快. 对应的最大有效控制角随负载流量的增加近似呈线性减小. 最大功率则在小流量时较小,而在流量变大时迅速增加至一个较高水平,并可在很大的负载流量范围内基本保持这一水平.

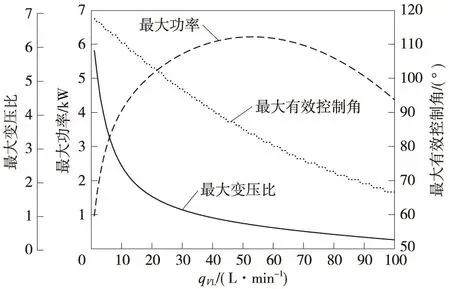
图9 液压变压器的最大变压比、最大有效控制角与最大功率

3 结 论

综上所述,本文中建立的数学模型在整个工作范围内都可以很好地描述液压变压器的变压比特性. 通过理论计算与试验得到下列结论.

① 在实际工作过程中存在的摩擦和泄漏使得负载流量对液压变压器的变压比特性有很大影响,液压变压器的变压比应表示为控制角和负载流量(或缸体转速)的函数.

② 当控制角为常数时,变压比随负载流量的增加单调减小,并且控制角越大,递减的趋势越剧烈.

③ 液压变压器存在最大变压比、最大有效控制

角度和最大功率,而且负载流量越大,液压变压器可以达到的最大变压比越小,相应的最大有效控制角也越小.

参考文献：

[1]van Malsen R A H, Achten P A J, Vael G E M. Design of dynamic and efficient hydraulic systems around a simple hydraulic grid, SAE Paper 2002-01-1432[R]. [S.l.]: SAE International, 2002．

[2]Peter P A J, van den Brink T L, van den Oever J, et al. Dedicated design of the hydraulic transformer[C/CD]∥Proc 3rd International Fluid Power Conference. Aachen, Germany: [s.n.], 2002．

[3]Achten P A J, Fu Z. Valving land phenomena of the innas hydraulic transformer[J]. International Journal of Fluid Power, 2000(1):39-47．

[4]Achten P A J, Fu Z, Vael G E M. Transforming future hydraulics: a new design of a hydraulic transformer[C/CD]∥The Fifth Scandinavian International Conference on Fluid Power (SICFP’97). Linköping, Sweden: Linköping University, 1997．

[5]欧阳小平.液压变压器研究[D].杭州:浙江大学工学部,2005．

Ouyang Xiaoping. Research on the hydraulic transformer[D]. Hangzhou: Faculty of Engineering, Zhejiang University, 2005. (in Chinese)

[6]欧阳小平,杨华勇,徐兵,等.新型配流副液压变压器研究[J].中国科学(E辑:技术科学)，2008,38(1):95-102．

Ouyang Xiaoping, Yang Huayong, Xu Bing, et al. Research on the hydraulic transformer with new distribution pairs[J]. Science in China (Series E：Technological Sciences), 2008,38(1):95-102. (in Chinese)