大旋转角坐标转换在沉石作业中的应用

刘忠喜 李全海 朱卫东

(同济大学测量与国土信息工程系, 上海 200092)

在大地测量和摄影测量中,坐标转换有着广泛的应用。如我国曾经采用北京54坐标系、西安80坐标系、以及目前即将普及的GS2000系统,如果想利用不同坐标系下测得的资料,必须进行坐标转换。另外，在GPS广泛应用的今天,WGS-84坐标系统与其他坐标系统的转换也越来越多。但是这些坐标转换都是小角度的,目前存在的主要转换模型是布尔莎七参数模型、莫洛金斯基模型以及武测模型等[1]。

然而在工程应用中,如沉石作业中,还存在大旋转角的坐标转换问题。对于这些坐标转换传统的方法是先将大角度问题转化成小角度问题,再利用小角度坐标转换模型进行处理[2]。另外,文献[3]提出了一种求解十三参数的方法,利用附有限制条件的间接平差原理，处理求解旋转矩阵和平移矩阵以及尺度参数。文献[4]中提出了一种形式上更为简便的方法,求解转换角度和平移参数等六个参数(尺度参数忽略)的方法。该方法是利用间接平差原理解算转换参数,计算模型简单,编程计算简便,精度评定容易。

在沉石作业中,所需放置的石块淹没在水下,需要通过观测固定在三个棱镜塔上的棱镜,来实时的控制水下沉放物的姿态,进而根据测量结果调整沉放物状态,直至满足设计值为止[5]。本文从沉石作业的流程与步骤、坐标转换模型以及精度评定角度作了简要介绍,并编程实现某工程算例计算,分析观测数据对于转换实时精度影响,最后从数字和图像角度表示计算结果,指挥沉放工作进行。

1 原理

1.1 沉石作业流程与步骤

海底沉石作业中测量工作主要有四项内容：沉放前的准备工作、浮运阶段的测量工作、沉放阶段的测量工作以及沉放后的测量工作[6]。其中,沉放前的准备工作包括：(1)控制网的建立。建立干坞控制网坐标系和沉放控制网测量坐标系,前者用来检测预制件的尺寸[7]，测定干坞坐标系下三个棱镜塔的棱镜与块体特征点之间的位置关系；后者用来测量沉放块体的姿态,指挥沉放工作进行。(2)安放棱镜塔和棱镜。在沉放块体上安装三座合适高度的棱镜塔并焊接棱镜,原则是安装要牢固,以满足棱镜与沉放块体特征点的刚体关系,并且使棱镜间的距离尽可能的大。(3)测量干坞中三个棱镜与块体特征点的坐标。

浮运阶段的测量工作比较简单,用计算机控制同步测量三个棱镜位置坐标,通过坐标转换计算水下块体的位置,将沉放块体运至沉放的大体位置。

沉放阶段的测量工作主要是在沉放块体浮运到大体的设计位置后,将块体精确的放置在设计位置,完成沉放工作。这个过程中测量的频率会大大增加,需要通过多次的沉放才能达到设计要求。

沉放后的测量工作是在块体沉放完成,待块体稳定后,借助测量棱镜塔上的棱镜,获取沉放块体特征点的位置,以备下次块体沉放时使用。

通过上述过程,可以看出沉石作业的关键是干坞坐标系与沉放坐标系之间的坐标转换。

1.2 坐标转换模型

在沉石作业坐标转换过程中尺度参数变化非常的微小,因此可以认为不存在尺度参数的变化[8]。采用文献[4]所提出的坐标转换模型

(1)

其中,(x0,y0,z0)T为坐标平移量,(x′,y′,z′)T为干坞坐标系中坐标,(x,y,z)T为沉放测量坐标系中坐标。三个旋转矩阵分别为

线性化后误差方程

(2)

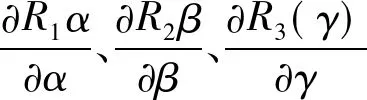
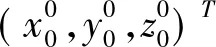
1.3 精度评定

根据间接平差[9]原理

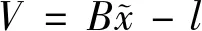
(3)

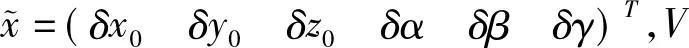
那么,未知参数的方差-协因数阵为

根据误差传播规律,可得转换点的协方差阵

其中,B′为需要转换的点构成的系数阵,构造方法同系数阵B相似,不再赘述。

2 算例

2.1 工程概况与编程实现

本文利用某港口工程沉石施工作业数据进行计算。工程概况如下：现有重约500 t的长方体块体需要沉放到设计位置(7、8、9),长方体块体可测量上表面的三点(1、2、3)坐标,并已知块体高为6 m。沉放位置由三个点控制,分别是7′、8′、9′。它们之间的相对关系如图1所示。

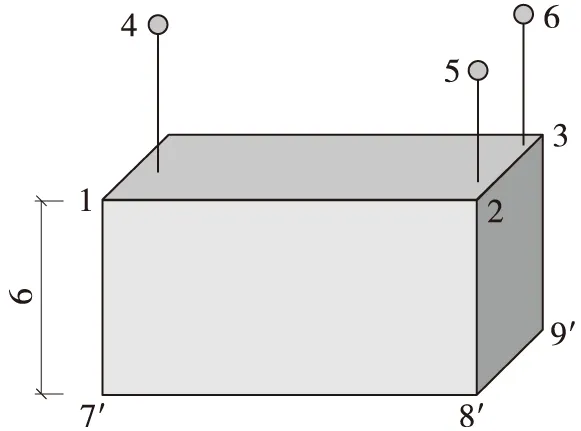
图1 沉放块体(单位：m)

编程实现：数据输入后由数据质量判断函数,判断是否满足坐标转换的条件。如果不满足,则返回数据输入,检查数据后重新输入判断。如果满足条件,进入下一步,利用干坞中棱镜坐标和沉放测量坐标系中三个棱镜坐标,进行六参数平差求得坐标转换六参数。接下来计算平移参数旋转参数并计算将沉放块特征点坐标。求得转换坐标后,经过正交条件平差和法向量归算求得长方体块的下表面角点坐标并与设计坐标(假设为最后一次沉放求得坐标)相比较[10]。

上述过程如图2所示。

图2 沉放程序计算流程

2.2 数据分析

在数据分析方面,先分析单次测量的数据结果及精度,然后分析几次转换中的大量数据所表现的规律。

第10次观测的计算数据：

旋转矩阵R与平移矩阵T分别为

R=

单位权中误差δ0=0.007 1 m

R阵的数值大小分布正好验证了转换的两个坐标系Z轴指向基本一致。

转换后的新坐标(x,y,z)与设计坐标的差值(Δx,Δy,Δz)如表1。

表1 实际坐标及设计坐标与实际坐标差值 m

由于坐标转换后需一步计算从而得到相应的下表面点的坐标,此过程又分为正交条件平差和向量的叉乘来计算法向量,相比之下对于精度影响很小,因此可以认为转换精度也就是最终的点位精度。转换点的点位中误差

m7′=0.043 2 mm8′=0.042 7 mm9′=0.041 7 m

以第8′点为例,列出部分观测的坐标转换各分量中误差、实时点位中误差及控制点单位权中误差(如表2)。

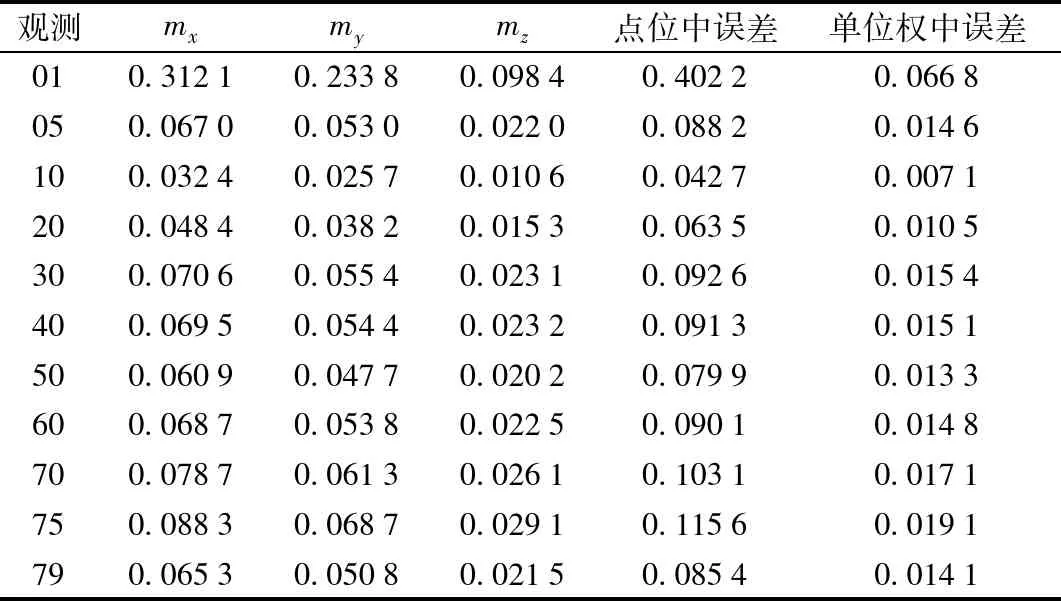
表2 部分次数观测的坐标转换的坐标分量中误差、点位中误差及单位权中误差 m

从表2可以看出,待定转换点的点位中误差大都在0.090 m附近,偶尔有较大的点位误差,因此可以认为此次沉石的点位中误差为9 cm。坐标误差分量方面,X、Y方向的误差分量是Z方向误差分量的3倍左右,这是因为Z轴指向转换前后基本不变,旋转分量较小的缘故。另外点位误差的值范围在0.042 7～0.402 2 m之间,因此实时精度是指挥沉放作业所必需的依据。

结合观测数据的质量来分析转换的点位精度,相邻棱镜点的观测边长与干坞中的相应边长差值(如表3)。L45表示棱镜点4与5的边长,其他类似。dotL45表示当前观测45边的边长与干坞坐标系中相应边长之差,其他也类似。

表3 相邻棱镜点边长及其与相应干坞边长差值 m

从表3中可以看出,受海上风浪、水汽等因素的影响,棱镜的观测坐标的质量起伏较大。经过相互比较后,可以知道：边长最大差值为第01次观测的dotL46=0.120 9 m,最小差值第079次观测的dotL46=0.001 1 m;三条边中,L56边边长变化相对较大,是导致转换精度不高的主要原因。其中第10次观测3条边长差值最小,转换质量应该最好。从表2中可以知道,无论从单位权中误差还是点位中误差角度,该次转换精度都是最好的。可以断定,棱镜坐标的观测质量优劣直接影响着转换的精度好坏。因此应当选择风浪较小、海面较平静的晴朗天气进行沉放工作,沉放的效果更佳。

2.3 数据显示

为了方便沉放块体指挥工作,将设计坐标和实际坐标的相对位置通过图像显示出来。下面是第01次(图3)和第79次(图4)的设计坐标与实际坐标的相对关系。设计坐标为7、8、9,实际坐标为7′、8′、9′。其中,x轴正向为竖直向上,y轴正向为水平向右。

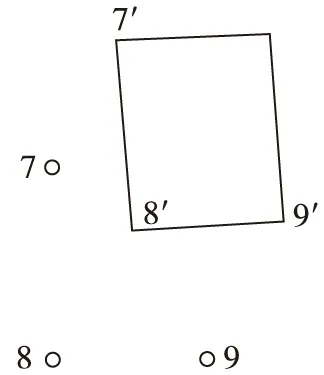
图3 第01次观测设计坐标与实际坐标关系

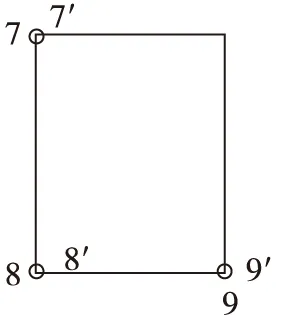
图4 第79次观测设计坐标与实际坐标关系

3 结论

对海底沉石作业过程进行了简要介绍,并对某工程作业过程加以编程计算,从测量的角度和实际应用的角度,对于计算的数据加以分析,给出计算结果做实时精度评定,为指挥沉放作业提供依据,并且分析影响测量精度的主要因素是棱镜中心观测值的质量。通过对设计数据与实测数据进行形象显示,指挥沉放工作进行,对于沉石作业施工,有一定的参考价值和意义。

[1] 刘大杰,施一民,过静珺.全球定位系统(GPS)的原理与数据处理[M].上海：同济大学出版社,1996：183-187

[2] 赵思齐.用于沉管施工的实时定位系统开发及应用[D].上海：同济大学，2007：12-20

[3] 陈义,沈云中,刘大杰.适用大旋转角度的三维基准转换的一种简便模型[J].武汉大学学报(信息科学版),2004,29(12)

[4] 王解先,季凯敏.工业测量拟合[M].北京：测绘出版社,2008：31-33

[5] 李全海,何 青.海底沉管隧道安放测量[J].海洋测绘,2004(6)

[6] 李全海.海底沉放结构物的位移监测[J].海洋测绘,2005(6)

[7] 李全海.海底沉管对接测量[J].同济大学学报(自然科学版),2005,33(12)

[8] 许 琛,王解先.沉管沉放的实时监测[J].工程勘察,2001(4)

[9] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社,2003：102-120

[10] 王解先,许 琛,陆彩屏.沉管沉放的实时监测[J].测绘学报,2002,31(5)