全站仪竖井联系测量的平差计算原理及其精度分析

何 波 刘成龙 黄志伟 赵梦杰 姬晓旭

(西南交通大学土木工程学院, 四川成都 610031)

竖井联系测量的目的就是将地面控制网的坐标、方位及高程按要求的精度准确地传递给地下隧道施工控制导线,为施工提供控制依据,以保证各相向开挖面能正确贯通。竖井联系测量采用的方法,主要有陀螺定向法、钻孔投点法、联系三角形法和导线定向法。其中,传统的联系三角形法是以前国内地下隧道竖井联系测量中最常用的方法,但由于该法存在设备笨重、工序繁多、工作时间长、劳动强度大和效率低等不足,目前使用较少。由于全站仪的普及应用,文献[1]提出了一种应用全站仪进行竖井联系测量的新方法,但其计算仍采用传统的方法,因而结果仍然是近似的,而且无法进行精度评定。

1 竖井联系测量的新方法

传统的竖井联系测量是用钢卷尺丈量联系三角形的各边,用经纬仪测量联系三角形的各角,这种方法不仅操作复杂而且效率低,不适应现代工程建设的需要。全站仪测量技术的日趋完善,使得我们可以通过在吊锤线上固定反射片,并采用ATR(自动目标识别)技术来测量联系三角形各边的水平距离和角度,这就是竖井联系测量的新方法。新方法大大减少了联系三角形各边的测距误差,且速度快、适应能力强,从而提高了竖井联系测量的精度。

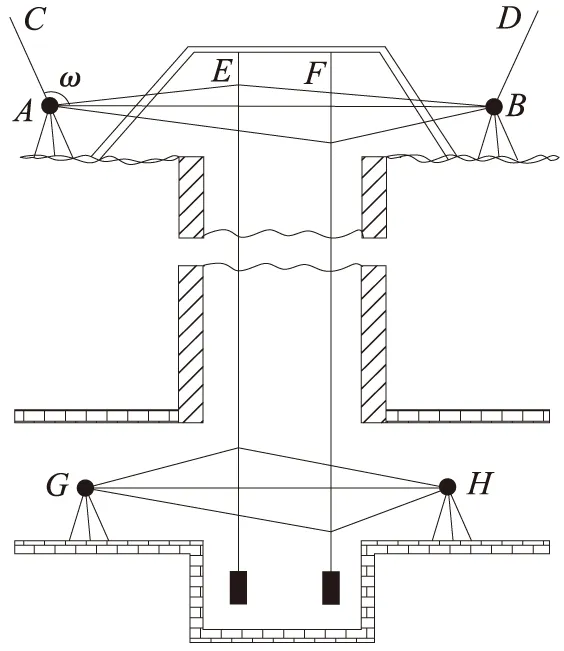
图1 全站仪竖井联系测量原理剖面示意

如图1所示,新方法在进行联系测量时,首先需要在井上井口附近埋设两个近井点A、B,并按照规定的精度,将竖井附近地面控制点的坐标,引测到A、B上；然后在竖井内悬吊两根吊锤线E、F,吊锤线E、F的间距应尽可能地大,在吊锤线的上、下适当部位固定塑料反射片；最后,在井下埋设两个地下导线的起算点G、H,通过竖井联系测量把地面点A、B的坐标和方位传递到地下G、H点上。

如图2所示，新方法在井上测量时,全站仪分别架设在近井点A(B)上,采用双测站极坐标测量的方法,测量测站A或B到E、F、B或A的方向值和距离,如果条件允许,则在井上测量时,还可测量A到控制点C和B到控制点D的方向值；如图3所示，新方法在井下测量时,全站仪分别架设在G或H点上,测量测站G或H到E、F、H或G的方向值和距离；不论是井上还是井下,距离测量全部为全站仪对反射片的直接测距,而不是传统的钢尺量距。

2 新方法的平差计算原理

2.1 井上联系测量误差方程式的开列

图1中的井上联系测量实际上是应用了两边连接的联系三角形,对这种图形需要观测A至C、E、B、F以及B至D、E、A、F的方向值，以及边AE、AF、BE、BF的平距。井上联系测量原理如图2所示。

图2 竖井联系测量井上测量原理示意

为了对井上联系测量观测数据进行平差计算,首先需要计算出E、F两点的近似坐标。由已知点A的坐标和观测角ω以及观测边SAE,可以计算出E点的近似坐标

(1)

式(1)中,XA、YA为A点的坐标值；αAE=αAC+ω。同理,可以计算F点的近似坐标。

由已知点A、B的坐标和待定点E、F的近似坐标,可计算待定边的近似坐标方位角α0和近似边长S0。由文献[2]可知,当计算出了各边的近似坐标方位角和近似边长后,即可按照式(2)和式(3)计算水平方向和距离观测值误差方程中的系数,进而开列出如下形式的水平方向和距离的误差方程

(2)

上式中ni为i测站上观测的方向数。

另外,ij边水平距离的误差方程式为

(3)

式(3)中,Sij为ij边的边长观测值,其他符号的意义同式(2)。

2.2 井下联系测量误差方程式的开列

井下联系测量原理如图3所示,测量时需要观测G或H到E、F、H或G的方向值和平距,因此井下部分的观测值个数n=11。

图3 竖井联系测量井下测量原理示意

为了计算G、H两点的近似坐标,可先解算图3中的三角形,得到δ1和δ2角度值,然后根据EF边的坐标方位角,推算出FG、EH边的近似坐标方位角,再仿照式(1),根据E、F点的坐标计算出G、H两点的近似坐标,进而再按照式(2)和式(3)开列出井下联系测量水平方向和距离观测值的误差方程。

2.3 观测值权值的计算

井上和井下联系测量的环境虽然有较大的差异,但由于竖井联系测量时边长都较短,同时若采用具有自动照准功能的全站仪进行观测,则在定权时可不考虑环境因素的差异,用相同的公式对井上、井下的观测值进行定权。

由于井上和井下的测量都存在两类不同类型的观测值,因此可按照经验定权法确定水平方向和距离观测值的权比关系,即以全站仪标称的水平方向观测值L的中误差mL为单位权中误差σ0,则距离和水平方向的权分别为

(4)

式(4)中，a和b分别为全站仪测距固定误差和比例误差,可由全站仪的标称精度得到。

2.4 平差计算的精度评定

(5)

(6)

利用式(5)求得的协因数可求得G点和H点X方向和Y方向的中误差及其点位中误差,利用式(6)求得的协因数，可求得井下导线起始边GH的坐标方位角中误差,计算公式如式(7)所示

(7)

式(7)中σ0为单位权中误差。

坐标传递的误差使得地下导线的各点产生同一数值的位移,其对横向贯通精度的影响是一个常数；而方向角传递的误差,将使地下导线各边方向角转动同一个误差值,它对横向贯通精度的影响将随着导线长度的增大而增大,是影响隧道贯通的主要误差源[5]。因此，在进行竖井联系测量的精度分析时,主要关注的是井下导线起始边坐标方位角的精度。

3 竖井联系测量的精度分析

3.1 井上联系测量精度的仿真分析

在井上进行测量时,虽然布网较为灵活,但有时受环境限制,并不一定能布设成伸展形状的联系三角形。因此，在传统的两边连接的联系三角形(图4中网形1)的基础上,提出了图4中的网形2。网形2中,两吊垂线E和F的连线方向和AB的方向也基本一致,所不同的是A、B两点在EF边的同侧。

图4 井上测量时不同网形

假设图3和图4中α1=α2=γ1=γ2=2°,δ1=δ2=3°且EF=5 m,先进行井上联系测量的精度分析,故只变化图4中β1和β2,且假设井下网形为图3中的网形,并令水平方向和距离的先验观测精度分别为±0.5″和±(1+1×10-6D)mm/km、±1.0″和±(1+2×10-6D)mm/km、±2″和±(2+2×10-6D)mm/km时,可按式(1)～式(7)计算不同网形情况下,井下导线起始点G、H的点位中误差和井下导线起始边GH的方位角中误差,计算结果如表1所示。

表1 井上联系测量精度仿真计算结果统计

表1中mG和mH分别为G、H两点的点位中误差,单位为mm；mGH为GH方向的方位角中误差,单位为″。

根据表1可以看出：

(1)在仪器精度相同且β1=β2的情况下,图4中两种网形GH边的方位角精度并无显著性差异。

(2)仪器精度、β1和β2角度大小对井下导线起始点G、H精度的影响不显著,但对GH边的方位角精度影响非常显著。

(3)当β1=β2=3°时,网形1计算出的井下导线起始边的精度优于网形2,但当β1=β2=10°或15°时,网形1计算出的井下导线起始边的精度低于网形2。通过分析可知,这是由于当β1和β2都为小角时,网形1和网形2的GH、EF、AB的方向都可基本保持一致；当β1和β2的增大时,网形1中AB的方向和EF、GH的方向相差越来越大,但网形2中GH、EF、AB的方向任然基本一致。

(4)β1和β2为小角对竖井联系测量更为有利,因为这能让EF的方向和AB的方向基本一致。

(5)井下和井上测量网形相同对竖井联系测量更为有利。

3.2 井下联系测量精度的仿真分析

受环境限制,井下联系测量的图形一般只能是图3,且图3中δ1和δ2角实际不可能很大,仍假设图3和图4中α1=α2=γ1=γ2=2°,β1=β2=3°且EF=5 m,变化δ1和δ2,假设的先验观测精度与井上相同,可按式(1)～式(7)计算井下导线起始点G、H的点位中误差和井下导线起始边GH的方位角中误差,计算结果如表2所示。

表2 井下联系测量精度仿真计算结果统计

从表2还可以看出：δ1和δ2为小角对竖井联系测量更为有利,因为这能让EF和AB、GH边的方向基本一致,从而使GH边的方位角中误差更小。

4 结论

(1)不宜使用标称精度等于或低于±2″和±(2+2×10-6D)mm/km的全站仪进行竖井联系测量。

(2)竖井联系测量时,井上和井下的网形应当相似。

(3)角度α1、α2、β1、β2、γ1、γ2、δ1、δ2的大小对竖井联系测量的影响非常显著,实际测量时,这些角度越小越好。

(4)竖井联系测量时,应尽量保证AB、EF、GH平行。

(5)应在α1、α2、β1、β2、γ1、γ2、δ1、δ2都为小角的前提下增大EF的间距。

(6)竖井联系测量的数据宜采用平差的方法进行处理,这样做不仅速度快,准确可靠,而更有利于隧道横向贯通误差的正确预计。

[1] 姬晓旭,刘成龙,何 波.竖井联系测量的新方法及其应用[J].铁道勘察,2009(5)

[2] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社,2003

[3] 张正禄，等.工程测量学[M].武汉：武汉大学出版社,2005

[4] 刘成龙,杨友涛,徐小左.高速铁路CPⅢ交会网必要测量精度的仿真计算[J].西南交通大学学报,2008(6)

[5] 李青岳,陈永奇.工程测量学[M].北京：测绘出版社,1995

[6] GB50308—1999 地下铁道、轻轨交通工程测量规范[S]