分段基准线法轨道测量实践与精度分析

黄克辉

(中船勘察设计研究院有限公司, 上海 200063)

某特大型龙门吊轨道东西向轨距为172 m,南北向轨道长度为915 m,由于设备行进中出现“啃轨”现象,需要现场测量其两根轨道的准直度和两轨道之间轨距。因轨道长度和轨距很大,加之现场环境复杂,给测量工作造成了很大困难。

1 分段基准线法轨道测量实践

基准线法的原理是通过建筑物或平行于建筑物轴线固定不变的铅直平面为基准面,一般用来测定建筑物的水平位移。当基准线很长时,照准误差影响会增大。为了获得较高的观测精度,可以分段进行观测,即先测定基准线中少数分段点相对基准线的偏离值,再将它们作为起始点,然后在各分段中测定测点相对分段基准点的偏离值,最后归算到两端点的基准线上。

本次龙门吊轨道测量方案如图1所示：在平行于轨道西侧10 m处设置一条915 m长基准线AB,在AB基准线中点测定1/2分段点C,同理分别测定1/4分段点D、E,如此把915 m基准线分成4段,每段基准线长228.75 m。首先在分段基准线上定出相应P点,然后在P点设站拨90°角分别测量P到东西轨道的距离SE、SW,通过归算到AB求得轨道准直度,而P点处轨距SP=SE-SW。

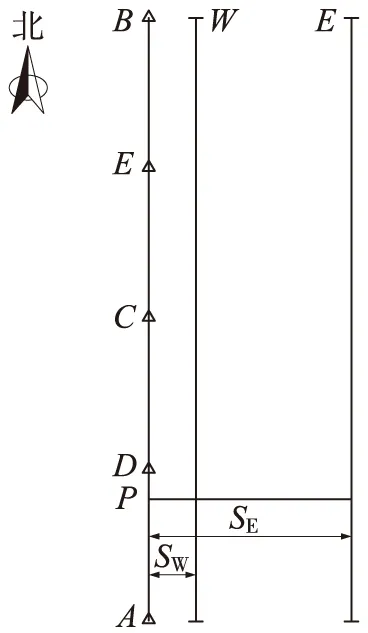
图1 轨道测量示意

由于基准线AB很长,分段点D、C、E与基准线AB会出现偏离值,通过角度观测测定D、C、E相对AB的偏离值,以使成果可以归算到AB基准线上,角度测量方案如图2所示。

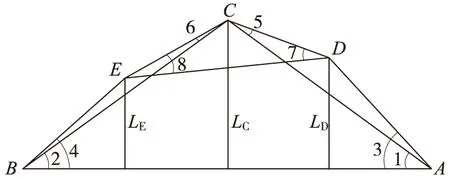
图2 角度测量示意

2 精度分析

轨道准直度由东西侧轨道相对基准线AB的距离确定,其精度由P点定位精度和距离SE、SW的测量精度决定。易知BE、EC段与AD、DC段相同,以下仅对AD、DC段测量进行分析。测角和测距采用莱卡TCRM1201+R1000型全站仪,仪器标称精度：测角1″,测距±(1+1.5×10-6D)mm(D为测量长度),望远镜放大倍数为v=30。为简化计算,以下分析未考虑测量对中误差影响。

2.1 分段点C、D、E偏离值测定精度

如图2所示,进行4测回测角,测角中误差为mα=±2″,用间接平差法列出误差方程

权1

权1

权4

权4

权4

权4

权4

权4

式中：LC、LD、LE为分段点C、D、E到AB的偏离值；Vi为观测角度对应的距离改正数；SAB、SAD、SDC、SCE、SEB为基准线相应段的长度,单位以km表示；mLC、mLD、mLE分别为LC、LD、LE测量精度。

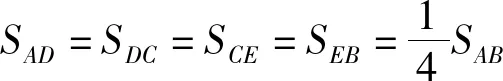
mLC=0.99SABmα=1.82 mm

mLD=mLE=0.93SABmα=1.71 mm

2.2 基准线AD段

以A为测站,D为后视点照准观测,纵向误差对测量的影响可忽略,主要考虑P点横向测定误差。P点测定误差主要来源是仪器照准误差mν和分段偏离值测定误差mLD,易知

P点对应处

式中β——视力临界角,根据经验值取β=15″；

ν——望远镜放大倍数,已知ν=30；

mP——P点相对于基准线AD的测量精度；

mSE、mSW——分别表示在P点到东西侧轨道长度测量精度；

mE、mW——分别表示P点对应轨道准直度测量精度。

将参数值代人计算式可得：mν=0.5″,mPmax=1.80 mm。

又mSE=1+1.5×0.01=1.015 mm,mSW=1+1.5×0.182=1.273 mm。

则最弱点mEmax=2.07 mm,mWmax=2.21 mm,也即准直度测量最弱点精度为2.07 mm和2.21 mm。

2.3 基准线DC段

以D为测站,C为后视点照准观测。P点测定误差主要来源是仪器照准误差mν和分段偏离值测定误差mLD、mLC,易知

同前所述,可得mPmax=2.56 mm,最弱点mEmax=2.76 mm,mWmax=2.86 mm。

3 结束语

采用分段基准线法进行轨道的准直度测量和轨距测量,精度可达到毫米级,如果提高测距测角精度或增加观测次数,可以进一步提高测量精度；为了提高测角精度,分段基准点测量应选择最佳观测时段进行。

[1] 李青岳，陈永奇.工程测量学[M].北京：测绘出版社,1997

[2] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉：武汉大学出版社，2003

[3] GB50026—2007 工程测量规范[S]

[4] JGJ/T8—2007 建筑变形测量规范[S]

[5] GB/T 15314—94 精密工程测量规范[S]

[6] 钱华清.采用激光经纬仪勘测船舶建造中的基准线[J].造船技术,2008(1)

[7] 赵玮霖，杨 惠，陈 康.直线度测量中利用基准线评定方法的探讨[J].重庆工学院学报(自然科学版),2007，21(1)

[8] 丁运华，王和平.钢丝基准线法井筒变形监测误差分析[J].矿山测量,2001(4)