基于边缘检测的快速斑点识别算法

谢丹桂 刘军清 孙水发 雷帮军

(三峡大学智能视觉与图像信息研究所,湖北 宜昌 443002)

老影视资料以其独特的方式见证并记录了世界的历史与现实、发展与进步、苦难与辉煌,是同时代文化工作者的艺术结晶,具有重要的历史价值与艺术价值.然而由于老影视资料胶片本身的化学物质非常容易老化,而且以往的保存技术落后,同时老影视资料在反复播放拷贝过程中也受到了不同程度的损伤.这样一来,现存的老影视资料能够正常播放的很少,出现了如:斑点、闪烁、抖动、褪色、划痕等缺陷[1-2].对保存下来的老影视资料进行修复并且重新保存到新的存储载体极为重要.

斑点是分布在电影画面中大小不一、形状各异的亮块或暗块.斑点作为老影视资料最主要的缺陷之一,对老影视资料画面质量的影响非常大,因此斑点的识别与修复具有重要的应用价值,其中快速准确识别斑点是修复的必要前提.研究表明,斑点可看作随机噪声.因此对斑点的检测主要依据斑点的空间连续性以及时间不连续性两个特征[3].

Kakaram[4]提出的斑点检测索引法(Spike Detection Index,SDI)将运动估计之后的前后帧与当前帧对应位置像素值的差值与阈值进行比较来判断是否为斑点.该方法仅利用了斑点时间不连续性特征,存在很多误识别.Nadenau M J[5]提出了等级差分斑点识别法(Rank Ordered Difference,ROD),该方法与SDI方法不同的是考虑了前后帧对应位置临近的像素与当前像素的差别,改善了识别效果.Tilie.S[6]采用了ROD的简化方法—简化的等级差分斑点识别算法(Simplified Rank Ordered Difference,SROD).该方法只用一个阈值.在阈值较小的情况下,该方法识别性能要好于 ROD,但同时误识别率要高一些.Gullu M K[7]在 2008年提出了一种两级SROD方法,该方法在阈值较小的情况下先采用一次SROD算法保证所有斑点都被识别出来,然后依据识别出的斑点位置矩阵,提高阈值,采用局部运动估计的SROD斑点识别算法排除误识别斑点像素.这种方法识别精度高,但因采用两次SROD算法,大大增加了时间复杂度.

上述算法都要对当前帧所有像素执行斑点识别算法,时间复杂度非常大.本文提出了一种基于边缘检测的快速斑点识别方法.与以往的SDI算法[4]、ROD算法[5]、SROD算法[6]以及Gullu MK 的两级SROD算法[7]不同,该算法利用边缘检测,将当前画面所有边缘(包括斑点的边缘和非斑点边缘)检测出来,然后依据边缘像素点,采用本文提出的正反扫描方法与局部运动估计的SROD算法完整地识别出所有斑点.该算法只需对边缘及其附近像素进行斑点识别就可以找到所有斑点,因此大大缩短了算法时间.同时斑点识别效果也有较明显改善.

1 基于边缘检测的斑点识别算法

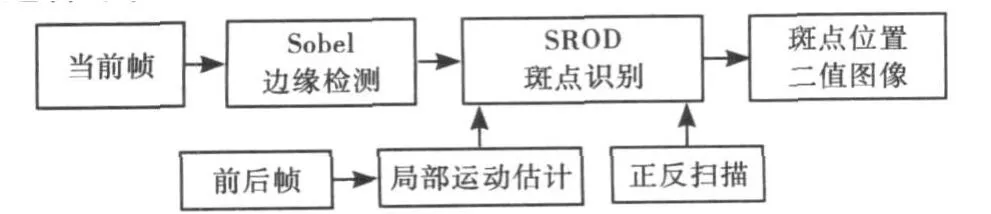
图1 本文提出的斑点识别算法框图

1.1 边缘检测算法的选取

根据斑点的特性,斑点与画面背景之间必会形成明显的边缘轮廓,同时画面其他对象也有边缘轮廓.边缘检测将斑点边缘与其他对象的边缘检测出来,如图1所示.只要获得斑点的部分边缘,再利用本文提出的正反扫描方法,就能找到斑点其它像素,包括未检测出来的斑点边缘像素.因此,本文对边缘检测精度要求不高,不需要用定位精度高但同时复杂度也很高的边缘检测算法,如Canny[9]算法.而是尽量选择时间复杂度小的检测算法.本文选择的是比较常用的Sobel[8]边缘检测算法.

1.2 局部运动估计的SROD斑点识别算法

边缘检测之后,得到的是边缘点位置的二值掩模矩阵.根据二值掩模矩阵中的边缘点位置,不仅要判断出斑点边缘,还要根据斑点边缘找到所有完整的斑点.本文采用提出的正反扫描方法结合局部运动估计的SROD进行斑点识别.正反扫描的过程与局部运动估计的SROD算法同时进行.正反扫描的思想是根据已识别到的斑点像素位置预测临近可能的斑点像素位置,局部运动估计的SROD算法既要从边缘点中辨别出斑点边缘点,又要对扫描过程中预测的斑点像素判断是否是真正的斑点像素.

由于边缘检测将斑点识别的范围缩小到边缘点附近,在进行斑点识别时就无需像以往的SROD算法一样,需要在识别之前对整个前后帧进行运动补偿.为进一步节省时间上的开支,本算法采用局部运动估计的SROD斑点识别方法.采用基于块的运动估计算法,这一思想首先出现在参考文献[7]中,只需对要识别的位置在前后帧对应的区域进行运动估计.与文献[7]不同的是,这里采用的块大小为3×1,而不是2×2或4×4.原因是SROD算法采用了前后帧与当前像素位置上下相邻的元素作为算法的输入,因此采用3×1的块运动估计可以与SROD算法很好地结合起来,减少了矩阵变换过程,从而节省了时间开销.

SROD斑点识别算法原理利用了斑点的空间连续性与时间不连续性特性.首先需要构建一个向量p(x,y,t),p(x,y,t)由经过运动估计后的前后帧6个像素的像素值组成,如式(1)所示.在局部运动估计的SROD算法中,不是前后帧所有的像素都进行运动补偿,只有待识别的位置的点对应在前后帧中的6个像素在识别时需要进行运动补偿.

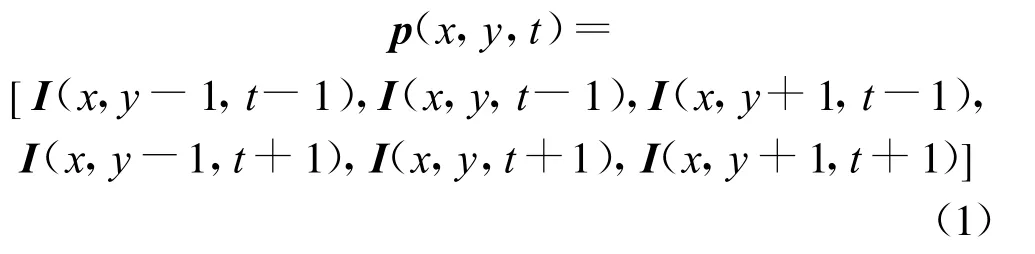
式中,x,y表示待识别像素值的坐标值;t表示当前帧,t-1,t+1分别表示前一帧和后一帧;I(◦)表示对应帧对应像素的灰度值.对p(x,y,t)向量进行如下操作

若SROD(x,y,t)大于阈值 T,当前点被判为斑点,否则为非斑点像素.阈值T的设置采用自适应的方法,即根据当前帧图像的灰度信息平均值与运动量大小来自动调整 T的大小,该思想最初出自文献[4].

1.3 正反扫描方法

首先,掩模矩阵存储的是边缘检测之后的结果,也就是掩模矩阵中像素值为1的点对应于当前帧的像素是边界点像素.正扫描过程如下:

从上往下,从左往右,依次扫描掩模矩阵.忽略掩模矩阵中值为0的点.掩模矩阵中值为1的点,对当前帧相应位置的像素做局部运动估计的SROD斑点识别.若确认当前像素为斑点像素,则对掩模矩阵中当前位置的邻近像素(如图2(a)中箭头所指位置像素)的像素值赋1.对应于这些位置的当前帧中的像素作为待识别的像素.这些待识别的点,在后续的扫描过程中利用局部运动估计的SROD算法做进一步判断.若局部运动估计的SROD斑点识别算法确认当前像素为非斑点像素,则对掩模矩阵中当前位置的像素值赋0.

通过不同数量处理器的反复试验数据分析，得到的结论是处理器的数目从少到多的递增，对应的收敛值越小，但计算时间是先减少，后增加。在试验中，当处理器的数量为4时，收敛值时间花费是最少的。处理器的数量再递增到6，所花费的时间并非减少，反而是增加，原因是处理器数量增加，并行蚁群算法的处理器间进程信息传递及通讯时间花费增大，因而使得总的计算花费时间增加。对于收敛值随着处理器的增加而减少的结果，原因是处理器数量增加，算法的搜寻区域更大，尽管花费在搜寻的时间更多，但最优解却容易得到，可靠性更好。

扫描过程中,要进行局部运动估计的SROD斑点识别的像素包括边缘检测得到的边缘点和被判断为斑点的邻近的待识别点.与当前帧已被识别的区域对应的掩模矩阵区域中,像素值为1的点表明当前帧对应点为斑点像素点.当前帧未被识别的区域,对应掩模矩阵中像素值为1的点,一部分是边缘检测之后还未经局部运动估计SROD算法识别是否为斑点的边缘点,另一部分是已经被识别为斑点的邻近待识别点.扫描过程中,对邻近位置斑点像素预测依据的原理是斑点的空间连续性,即斑点像素附近的像素可能是斑点像素.

一般情况下,经过正扫描与局部运动估计的SROD斑点识别,所有斑点基本上能完整找到.但在边缘检测时,若最左或者最上方的边缘缺失,就有可能造成后面识别的斑点不完整.此时需要根据正扫描已经得到的斑点位置,也就是正扫描之后的掩模矩阵,再做一次反扫描.从下往上,从右往左进行扫描就能把整个斑点找出来,这时扫描的临接像素位置如图2(b)中箭头所指位置所示.

图2 扫描中的邻近像素

图3给出了本文提出的斑点识别算法对视频序列“永不消失的电波”中某一斑点帧的仿真结果,包括每一步的中间结果和最终斑点识别结果.这4个图分别是含有斑点的当前帧、当前帧的Sobel边缘检测结果的二值掩模矩阵图像、正扫描后斑点识别结果的二值掩模矩阵图像、反扫描后斑点识别结果的二值掩模矩阵图像.当前帧中用红色圈标记的白色不规则的亮块就是斑点.Sobel边缘检测结果的二值掩模矩阵图像中用红色圈标记的是相应的斑点边界.

图3 老电影视频序列“永不消失的电波”中的缺陷帧斑点识别结果

可以看出Sobel边缘检测出来的斑点边缘不完整,最上与最左边的边缘都有缺失,因此正扫描识别到的斑点也不完整,需要反扫描才能得到完整的斑点.经过上面Sobel边缘检测、正反扫描以及局部运动估计的SROD斑点识别等步骤,最终得到本文提出的斑点识别算法的流程图如图4所示.

2 实验结果及分析

本文将提出的算法与SROD斑点识别算法[6-7]中Gullu MK提出的两级SROD斑点识别算法识别结果进行了比较.算法在 PC机(处理器 Intel Core Duo、主频1.83GHz、内存1G)上实现.表1给出了各个斑点识别算法在时间复杂度上的比较结果,所用斑点视频帧来源于5个不同的老电影视频序列.图5、6中只给出了其中两个序列的斑点帧斑点识别视觉对比效果.实验中的所有斑点均为老电影中实际存在的斑点.

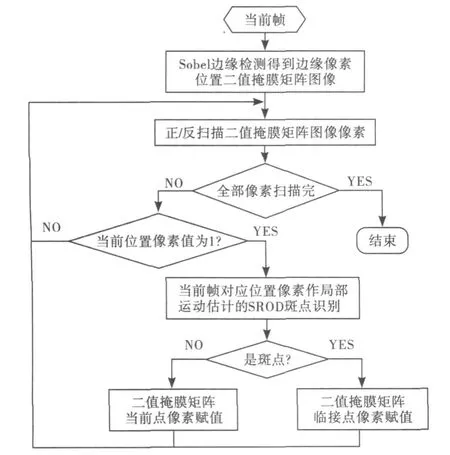
图4 本文提出的斑点识别算法流程图

图5 视频序列“刘三姐2”中斑点帧3种斑点识别算法识别视觉对比效果

图5、6分别是刘三姐2、松花江上这两种视频序列中斑点帧的三种斑点识别算法识别效果的视觉对比.针对每个视频序列,4个图像依次为,含有斑点的当前帧、SROD算法识别结果、Gullu MK的两级SROD算法识别结果、提出的算法识别结果.从图5、6可以看出,SROD算法存在很多误识别,Gullu MK的两级SROD算法识别精度高、效果明显优于SROD算法.而提出的算法的斑点识别效果几乎可以同两级SROD算法媲美.

图6 视频序列“松花江上”中斑点帧3种斑点识别算法识别视觉对比

由表1可以看出,Gullu MK提出的两级SROD算法虽然识别效果好,但时间复杂度最高.提出的算法的时间复杂度远远小于Gullu MK的两级SROD算法的以及SROD算法的.跟SROD算法相比,本文提出的算法所消耗的时间比SROD算法所耗时间的1/2还要少,甚至是SROD算法的1/4.

表1 3种算法时间复杂度比较(单位:s)

观察3种算法时间复杂度以及视觉效果可以看出,SROD算法存在很多误识别,Gullu MK的两级SROD算法虽然取得了比较好的识别效果,但是由于采用了一次SROD算法加上一次局部运动估计的SROD算法的模式,时间复杂度非常高.本文提出算法不仅在效果上几乎可以达到两级SROD的性能,而且时间复杂度远远小于SROD算法以及两级SROD算法.

提出的算法基于边缘检测的思想将识别范围集中到边缘区域,同时也缩小了运动估计误差带来的误识别范围,误识别一般只会出现在边缘区域.这也是从某种程度上来说,新的算法识别视觉效果要好于SROD斑点识别算法的原因之一.其次,局部运动估计的SROD检测算法在运动估计的时候考虑了局部小范围的运动,而且本文中提出的算法运动估计中采用3×1的块大小,相对于SROD算法的4×4的块匹配更精确,这也是识别效果更好的原因.

在时间复杂度上,提出的算法占绝对优势的原因是:一是因为基于边缘检测的思想将识别范围集中到边缘区域,缩短了识别时间;二是采用局部的运动估计,无需对整个前后帧进行运动估计,只需对边缘点及其附近的可能是斑点的像素点进行运动估计,进一步缩短了时间.

3 结 论

本文提出了一种基于边缘检测的斑点识别算法.利用边缘检测将斑点识别范围缩小到边缘附近,并且将局部运动估计的优势有效地应用到提出的算法中,与文中的扫描方式相结合,大大减少了时间复杂度,取得了很好的斑点识别效果,非常适合应用到工程实际中.如何进一步减少时间复杂度,提高斑点识别性能以及基于该算法的斑点修复是下一步要研究的重点.

[1］堪安军.数字视频修复若干关键技术研究[D].北京:中国科学院研究生院,2006.

[2］陈 钊,关景火,徐 进,等.基于小波分解的电影胶片划痕损伤数字修复技术[J].中国图象图形学报,2006,11(11):58-63.

[3］SaitoT,Komatsu T,Ohuchi T.Practical Nonlinear Filtering for Removal of Blotches from Old Film[M].Proc.Conf.Image Processing,1999(3):164-168.

[4］Kokaram A C,Rayner P J.A System for the Removal of Impulsive Noise in Image Sequences[M].International Conference on SPIE Visual Communications in Image Processing,Boston,M A,1992,322-331.

[5］Nadenau M J,Mitra S K.Blotch and Scratch Detection in Image Sequences Based on Rank Ordered Differences[M].Proceedings of the Fifth Internet Workshop on Time-Varying Image Processing and Moving Object Recognition.Florence,Italy,1996:1-7.

[6］Tilie S,Laborelli L,Bloch I.A Contrario False Alarms Removal for Improving Blotch Detection in Digitized Films Restoration[M].Processings of 14th Int.Workshop on Systems,Signals and Image Processing,and 6th EURASIP Conf.Focused on Speech and Image Processing,M ultimedia Communications and Services,M aribor,Sloveniar,2007:410-413.

[7］Kemal Gullu M,Oguzhan U,Sarp E.Blotch Detection and Removal for Archive Film Restoration[J].AEUInternational Journal of Electronics and Communications.2008,62(9):534-543.

[8］Jagadish P,Shambhavi D S.A novel Digital Algorithm for Sobel Edge Detection[J].Communications in Computer and Information Science,2010,70(6):91-95.

[9］Pawlak Z,Peters J F,Skowron A.Rough Measures Rough Integrals and Sensor Fusion[M].Rough Sets and Granular Computing.Berlin:Springer,2003,125(11):263-272.