不同极限状态下弦支筒壳结构的力学性能和可靠性能

陈志华，刘占省，乔文涛

(天津大学建筑工程学院，天津 300072)

当建筑功能要求结构具有较大跨度时，单层筒壳或厚度较小的双层筒壳由于其自身平面外稳定性差，难以实现较大的跨度，而采用厚度较大的双层或多层筒壳时，也存在用钢量多、支座水平推力大、节点构造复杂、施工难度大等缺点．为了克服现有技术的不足，以筒壳结构为基础，在弦支结构体系[1-4]的启发下，笔者提出了一种新的弦支结构——弦支筒壳(cable supported barrel vault，CSBV)．通过在筒壳结构的适当位置设置撑杆及预应力拉索形成弦支筒壳结构体系，使得整体结构刚度增加，降低了用钢量和结构施工难度，也减小了支座水平推力．

预应力钢结构已成为现代结构工程中最活跃最具有发展潜力的结构体系之一，但预应力钢结构许多领域尚待开发和研究[5]，其中之一就是预应力钢结构可靠度的研究．弦支筒壳作为一种新的结构形式，应基于概率的“以性能为基础”的设计思想，考虑整体屈曲、承载力、变形3种失效模式，从可靠性角度分析和评估其力学性能；分析弦支筒壳整体稳定性方面的可靠性并与单层筒壳进行对比分析，研究矢跨比、垂跨比和撑杆数目等主要参数的变化对结构可靠性的影响，确定合理的参数取值；以及分析预应力的改变对上述失效模式下结构可靠性的影响，从而为弦支筒壳等预应力钢结构的设计和分析提供理论和参考依据．

1 弦支筒壳结构体系及其预应力设计

弦支筒壳结构由上层筒壳、下弦拉索和中间撑杆组成，撑杆下端通过转折节点与拉索连接，撑杆上端与筒壳连接，拉索的两端通过锚固节点与筒壳连接，锚固节点一般设置在筒壳支座位置处，如图 1所示．弦支筒壳结构采用静力平衡法反复迭代来获得其最优初始预应力值．弦支筒壳结构的优点在于一方面改善了普通筒壳结构支座推力过大的问题，另一方面由于撑杆和预应力拉索的加入，使得单层网壳的面外稳定得到很大提高，从而使得单层网壳可以跨越更大的跨度，避免了采用双层网壳所带来的一些不足(如用钢量大、节点构造复杂等)，因此，弦支筒壳结构上部网壳一般采用单层或厚度较小的双层网壳．撑杆一般是沿跨度方向竖直排列的，设置的数目可根据跨度大小经计算优选确定．拉索沿筒壳纵向可每隔2个或多个网格布置一道，且拉索需要有一定的垂度布置．通过在筒壳结构的适当位置设置撑杆及拉索形成弦支筒壳结构体系，一方面由于拉索和撑杆的设置，使得整体结构刚度增加，解决了单层筒壳或厚度较小的双层筒壳由于稳定性差而难以跨越较大跨度的问题；另一方面，由于上部的筒壳结构采用单层或厚度较小的双层筒壳，降低了用钢量，结构施工难度也大大降低．同时，由于拉索的设置，可以在拉索内设置预拉力，减小支座水平推力，降低了下部结构的承载负担．

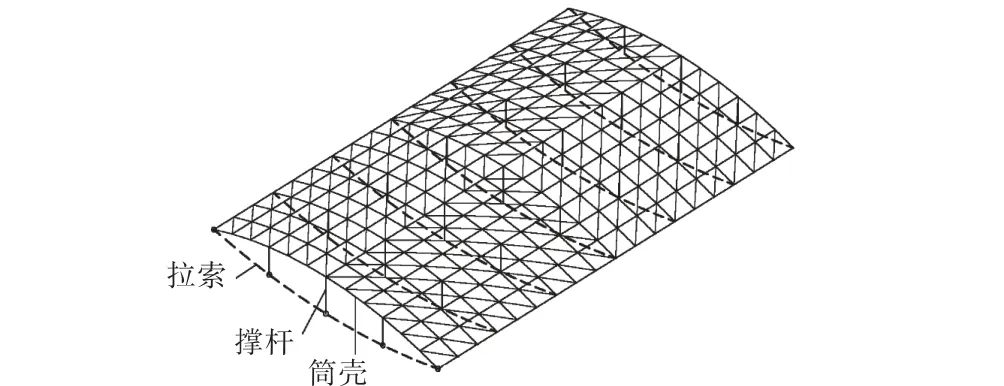
图1 弦支筒壳结构示意Fig.1 Cable supported barrel vault structure

弦支筒壳的周边约束方式一般采用空间简支，这样由筒壳结构产生的巨大的水平推力将被释放掉，而下弦拉索则用来限制所产生的较大的滑动位移．拉索中所要施加的预应力设计原则为：所施加的预应力应尽可能地将筒壳在屋面荷载作用下的各支座处的水平滑移消除，首先，不施加预应力，即各索段中的预应力为零，在屋面荷载和结构自重作用下求得索的内力为 N ={N1, N2, N3, N4, … ,Nn-1,Nn}，然后将此内力 N作为计算预应力分别施加在相应的索段中，调整计算预应力大小反复试算，最后使得水平滑移量尽可能逼近零，此时的计算预应力值即为目标值．

2 基于响应面的蒙特卡罗模拟方法

响应面技术是用一个超曲面来近似地替代实际的复杂结构输入与输出的关系．在保证计算精度的前提下，响应面法可以计算各种类型的非线性问题，且计算工作量可大大降低，因此响应面法非常适合大型复杂钢结构体系的非线性分析及其可靠性评价[6-8]．预应力钢结构的极限承载力 g(X)可表示为各随机变量X的二次超曲面，其形式为

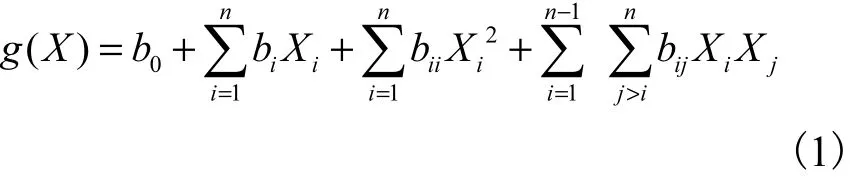
式中：Xi(i＝1，2，…，n)是i随机变量；b0, bi, bii,bij为响应面的待定系数．

本文方法的具体步骤如下：

(1) 确定性的有限元分析，创建分析文件；

(2) 定义随机输入变量和随机输出变量，确定输入变量服从的分布类型及其统计参数；

(3) 为了使抽样点数量较少但又能有效包含抽样空间的信息以保证响应面的精度，采用中心复合设计法进行试验设计，调用有限元程序，求解方程组，得到失效函数的拟合表达式并求解待定系数；

(4) 通过响应面试验设计进行回归分析，确定响应面方程的组成项及其系数；

(5) 用响应面方程代替有限元模型，采用蒙特卡罗法进行可靠度分析，从而得到结构的可靠度．

3 算例及统计参数的选取

3.1 工程算例

本工程为某地区的纺织厂车间，车间的屋盖部分采用了弦支筒壳结构，其长约 410,m，跨度为50,m．屋盖钢结构被分为独立的 4段，本文取其中一段进行计算，长度为 116.2,m．根据建筑要求，此工程弦支筒壳的矢高为 4.3,m，垂度为 0.7,m．单层网壳中有 5 种截面，分别为：Φ180×6，Φ203×8，Φ245×8，Φ299×8和Φ325×10；撑杆选用Φ273×10；下弦拉索采用半平行钢丝束Φ7×73．屋面恒荷载为0.80,kN/m2，活荷载为 0.5,kN/m2．结构立面图与平面图如图2和图3所示．

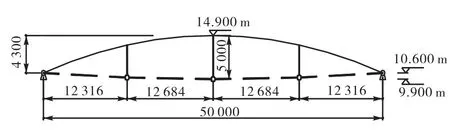
图2 立面示意(单位：mm)Fig.2 Elevational drawing (unit：mm)

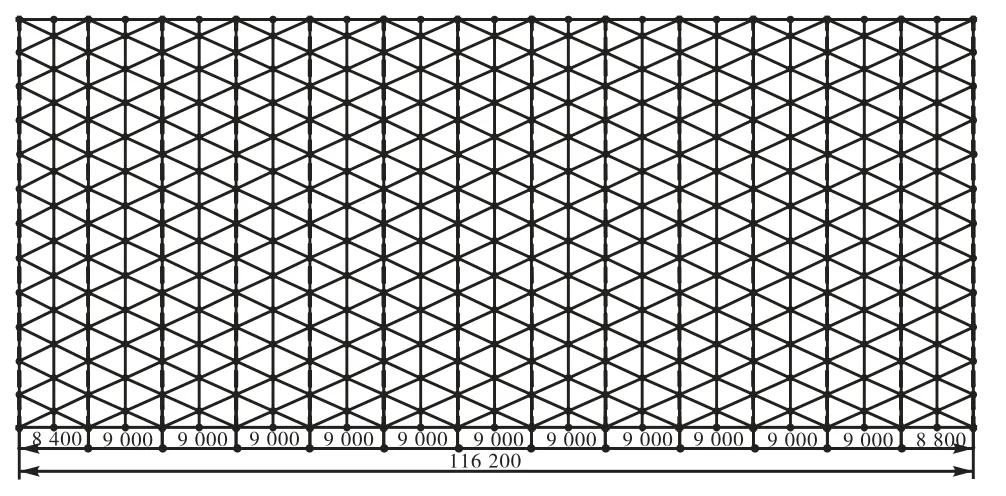
图3 平面示意Fig.3 Plane graph

3.2 随机变量的选取

为保证设计具有一定的可靠度，设计中所用荷载值、材料强度值、构件尺寸等都是满足一定保证率的标准值．进行可靠性分析，必须知道这些参数的真实分布．本算例中要用到材料属性及截面尺寸等随机变量的统计参数[9]如表1所示(D235×10～D273×10是弦杆和撑杆钢管型号)．预应力结构除永久荷载和可变荷载外，还有预应力荷载，是长期作用在结构上的荷载，其性质视同永久荷载，变异性接近可变荷载[5]．故假设本文结构中的预应力服从正态分布，变异系数为0.288，不同索的预应力大小分别为pre,3＝715,502,N，pre,4～pre,7＝1,266,057,N．

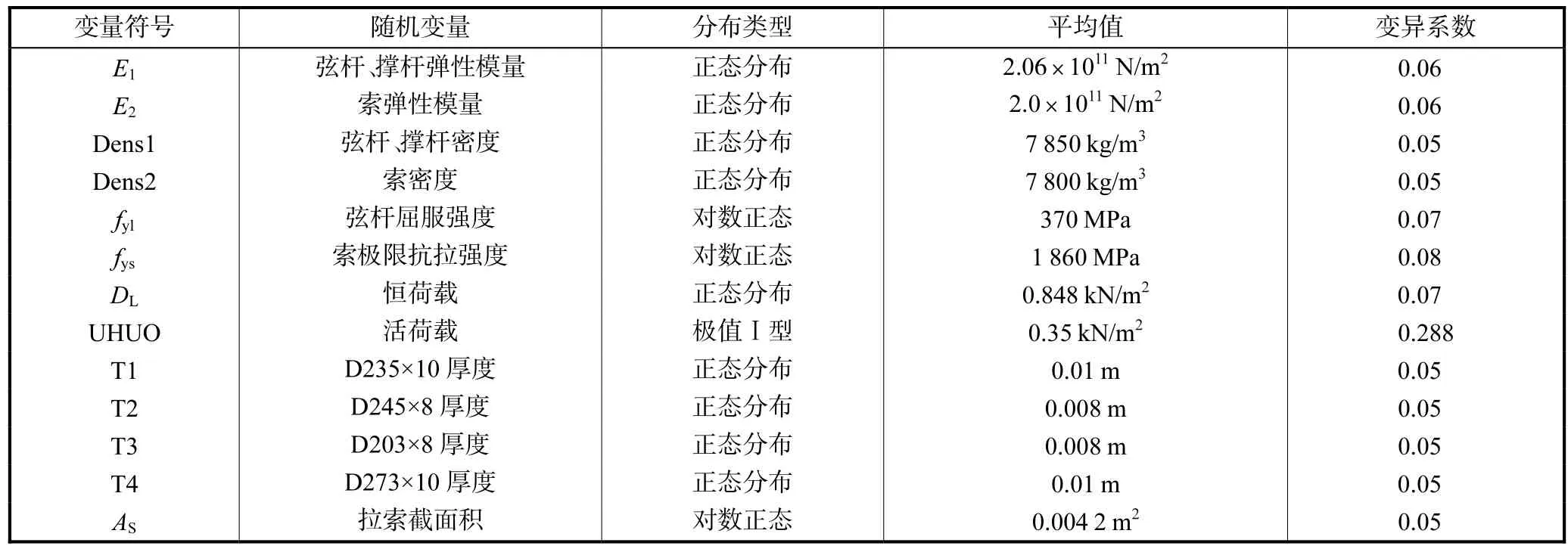
表1 随机变量的统计参数Tab.1 Statistical parameters of random variables

3.3 极限状态方程的建立

弦支筒壳结构体系的主要失效模式有整体屈曲失效、承载力失效和变形失效 3种．笔者分别针对上述3种情况，建立结构极限状态方程．

3.3.1 整体稳定控制

整体屈曲失效是指在荷载作用下，结构体系发生整体屈曲，从而使得体系破坏．进行网壳结构全过程分析求得的第1个临界点处的荷载值，可作为网壳的极限承载力．将极限承载力除以系数 k后，即为按网壳稳定性确定的容许承载力(标准值)．按照《网壳结构技术规程》(JGJ 61—2003)中的相关规定，系数k可取为 5．但是此安全系数的取值缺乏足够的统计资料和理论依据．目前，稳定系数取值的研究均局限在网壳结构，其成果不利于推广到普遍的、复杂的、各式各样的空间钢结构上，尤其是预应力钢结构，故本文整体稳定系数 k分别取 3、3.5、4、4.5和 5，建立极限状态方程为

式中：λ为稳定荷载比例系数；[]k为稳定系数．

3.3.2 承载力控制

承载力失效是指在荷载作用下，体系中某些杆件发生强度破坏或者杆件失稳，进而导致整个体系的破坏．预应力钢结构中的拉索强度设计值不应大于索材极限抗拉强度的 40%～55%，重要索取低值，次要索取高值[10]，本文取 45%．由于索是预应力钢结构中的关键构件，一般单个索的破坏也将导致结构的失效，对于索的承载能力失效概率，定义极限状态方程为

式中R、S分别表示拉索抗力及荷载效应，均为随机变量．

上弦杆强度极限状态方程和考虑撑杆受压屈曲的极限状态方程分别为

式中：RX、RC分别为弦杆和撑杆的抗力；SX、SC分别为弦杆和撑杆的荷载效应；φ为受压杆件的稳定系数．

3.3.3 位移控制

位移失效是指在荷载作用下，体系中的某些部位达到了位移的极限，导致结构体系不能正常使用．一般在确定的荷载类型下，结构的最大位移发生的位置都是确定的，所以变形失效一般只有一种失效模式．正常使用极限状态下，按照《网壳结构技术规程》(JGJ 61—2003)，结构的最大位移计算值u不超过短向跨度的1/400，故对于位移失效模式，相应的极限状态方程为式中：[]u为规范允许的最大结构位移；u为工作状态下结构中的最大位移；L为短向跨度．

4 弦支筒壳整体稳定性及其可靠性研究

单层网壳和厚度较小的双层网壳均存在总体失稳(包括局部壳面失稳)的可能性，设计某些单层网壳时，稳定性还可能起控制作用．弦支筒壳结构正是以单层网壳和厚度较小的双层网壳为基本单元的结构体系，所以，全面系统地对其进行稳定性能研究显得尤为重要．关于结构稳定性能的研究方法，以非线性有限元分析为基础的结构荷载-位移全过程分析[11]能将结构强度、稳定乃至刚度等性能的整个变化历程表示得十分清楚，因而可以精确地研究结构稳定性的问题．基于结构体系可靠度的稳定设计理论和分析方法是目前结构稳定研究的热点[8,11-12]，但目前可供实用的成果还较少．故本节首先从力学性能和稳定性能上对弦支筒壳进行了分析，然后在整体屈曲失效模式下，进行了弦支筒壳整体稳定性的可靠度分析和评估．

4.1 弦支筒壳与单层筒壳的力学性能比较

为了进行力学性能比较，以弦支筒壳标准模型为基础，保持其他条件不变，将拉索与撑杆去掉，变为单层筒壳结构进行计算．结构在屋面荷载及自重下，各自的主要计算数据分别列于表2中．

表2 结果比较Tab.2 Result comparison

从表2中可以看出，弦支筒壳结构不但消除了支座处的水平推力，并且使得支座处的水平滑移和结构的竖向位移减小，杆件的最大应力也很合理，能很好地满足设计要求．弦支筒壳结构克服了普通筒壳结构的不足，比较适合应用于大跨度空间建筑结构．

4.2 弦支筒壳与单层筒壳的稳定性能及其可靠性能

比较

仍以第3节中的弦支筒壳为基础算例，采用荷载-位移全过程分析方法，计算时取一致缺陷模态法为最不利缺陷，最大初始缺陷依据网格结构设计规程取跨度的1/300，荷载全跨布置，荷载作用形式选取全跨恒荷载+全跨雪荷载．应用ANSYS有限元分析软件对其进行稳定性分析；然后根据第 2节中的方法和步骤，编制 APDL计算程序，对结构进行了整体稳定性的可靠性分析．

为了验证编制程序的准确性，现以文献[9]中某题为例：一圆杆受拉力P的作用，试确定其极限承载力的可靠度指标．已知拉杆材料强度r及其直径 D为基本随机变量，P为常量，P＝50,kN．r、D相互独立且服从均匀分布，其均值方差分别为rμ=170,MPa，Dμ=29.4,mm，rσ＝24.99，Dσ＝2.998,8．文献给出的精确解β＝2.833,8，运用所编程序得到结构极限状态方程后，对该方程进行10万次抽样，得到的解1β＝2.848,5．1β与β的误差为0.5%，可见应用本文所编制的程序能够得到较精确的解．

结构的屈曲值和非线性屈曲临界荷载见表 3，结构的整体稳定性可靠度指标见表 4，结构的前 2阶屈曲模态见图 4和图 5；将下弦拉索与撑杆去掉，保持其他条件不变，变为普通筒壳结构，同样对其进行稳定性分析和可靠性分析，将二者分析得出的结果进行比较，分别见表3、表4和图6．

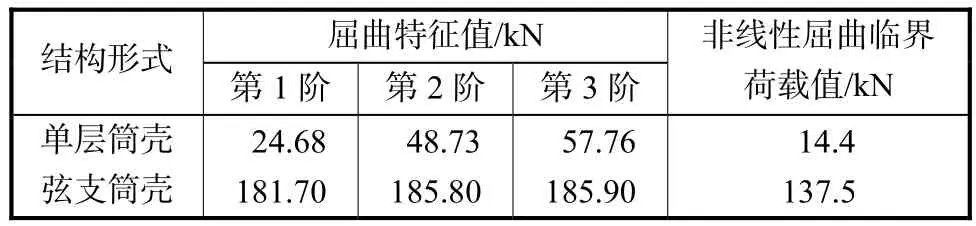
表3 弦支筒壳与单层筒壳屈曲值Tab.3 Buckling value of CSBV and single-layer cylindrical latticed shell

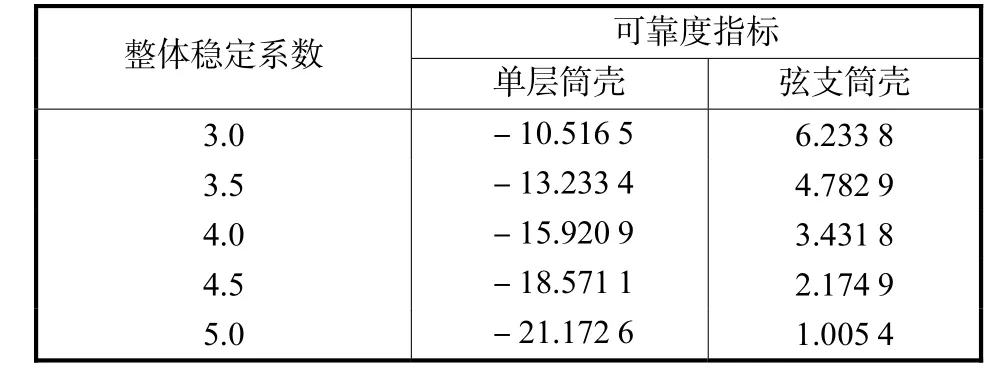
表4 弦支筒壳与单层筒壳可靠度指标Tab.4 Reliability index of CSBV and single-layer cylindrical latticed shell

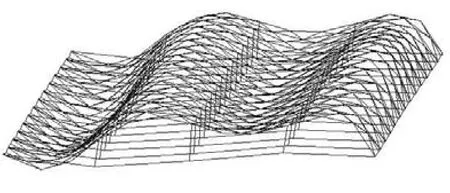
图4 第1阶屈曲模态Fig.4 Buckling mode 1

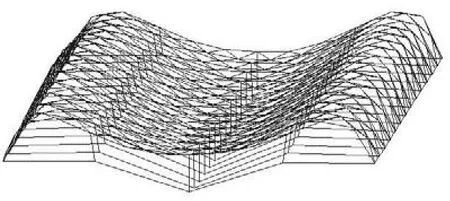
图5 第2阶屈曲模态Fig.5 Buckling mode 2

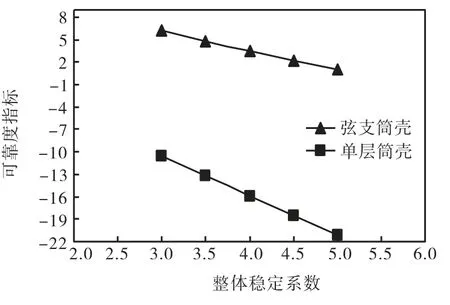
图6 可靠度指标比较Fig.6 Reliability index comparison

从图4可以看出，弦支筒壳失稳形式基本呈现为沿跨度的波状失稳，以第 1阶屈曲模态为例，屈曲形态大致为沿跨度方向的 2个全波，与单层筒壳相比(其失稳形式亦为沿跨度的波状失稳，第 1阶屈曲模态呈现为沿跨度方向的 1个全波)，二者的屈曲形态近似，这是由于弦支筒壳的基本单元为单层筒壳，但弦支筒壳的屈曲形态更加密集(2个全波)，这是由于增加撑杆和预应力拉索后，使得结构的整体刚度分布更加均匀．

从表3中可以看出，弦支筒壳的屈曲特征值和非线性屈曲临界荷载值均比单层筒壳大幅度提高，第 1阶屈曲特征值提高了6.36倍，非线性屈曲临界荷载值提高了8.55倍，说明下部撑杆和预应力拉索大大改善了单层筒壳的稳定性，弦支筒壳具有较好的稳定性．从表4和图6可以看出弦支筒壳的整体稳定性的可靠度指标比单层筒壳的可靠度指标有大幅度提高，如稳定系数[]k为3时，弦支筒壳整体稳定性可靠度指标为 6.233,8，而单层筒壳为-10.516,5，这也说明下部撑杆和预应力拉索大大改善了单层筒壳的稳定性．

5 主要参数对弦支筒壳结构可靠性的影响

在结构设计中，不仅要保证结构在极端荷载下的安全性(相应的失效模式为承载力失效)，还要满足结构适用性要求(相应的失效模式为位移失效)．由于弦支筒壳结构的矢跨比、垂跨比、撑杆数目是影响结构性能的几个主要参数，故本节仍以第3节中的弦支筒壳为标准计算模型，分析上述参数的改变对结构安全性和适用性方面的影响．由于不同大小的网壳当尺寸比例相同时，其性能具有相似性，所以参数分析中只设定一种筒壳的跨度(即跨度 L为 50,m)．由于主要研究结构的静力性能，故荷载工况只选取1.2恒荷载+1.4活荷载．仍采用本文所编制的计算程序来实现弦支筒壳结构的可靠度分析．

5.1 矢跨比的影响

以弦支筒壳标准模型为基础，改变结构的矢高，其他参数不变，研究其对弦支筒壳结构可靠性的影响．本文分别对矢跨比为 0.06、0.086、0.12和 0.15四种情况进行了分析，此时可靠度指标随矢跨比变化的曲线如图7所示．

弦支筒壳标准模型的矢跨比为 0.086，垂跨比为0.014，撑杆数目为 3．由图 7可知该标准模型受拉索、撑杆和弦杆承载力以及位移控制的结构可靠度指标分别为 3.90、12.96、7.42和 0.06，可见位移失效模式起主要控制作用．由图 7可知，随着矢跨比的增大，拉索、撑杆和弦杆承载力以及位移控制的结构可靠度指标均呈增大趋势．这是由于矢跨比的增加，结构受力由原来的“梁”的特性逐渐变为“拱”的特性．在进行弦支筒壳的设计时，矢跨比过小会使结构扁平、刚度变弱，如矢跨比为 0.06时，受最大位移控制的可靠度指标为负值，不再满足《建筑结构可靠度设计统一标准》(GB 50068—2001)要求，若要改善这些缺陷，需要大幅度地增加拉索的预应力，使结构过多地承受预应力所带来的负担，截面设计过大而不经济．但若矢跨比取得过大，则下弦拉索会对上层筒壳的约束作用减弱，无法发挥弦支的作用．由图 7也可看出，若既要满足建筑要求又要考虑到结构的经济适用性，弦支筒壳结构矢跨比取值在0.08～0.12为宜．

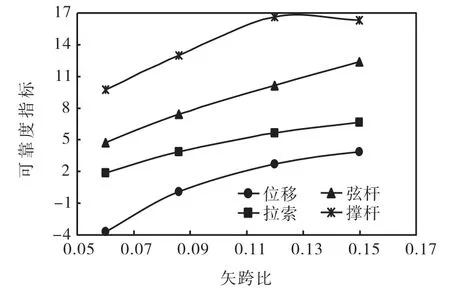
图7 矢跨比对结构可靠度的影响Fig.7 Influence of rise-span ratio on structure reliability

5.2 垂跨比的影响

以弦支筒壳标准模型为基础，改变结构的垂度，其他参数不变，研究其对弦支筒壳结构可靠度的影响．本文分别对垂跨比为 0.014、0.03、0.05和 0.08四种情况进行了分析，此时可靠度指标随垂跨比变化的曲线见图8．

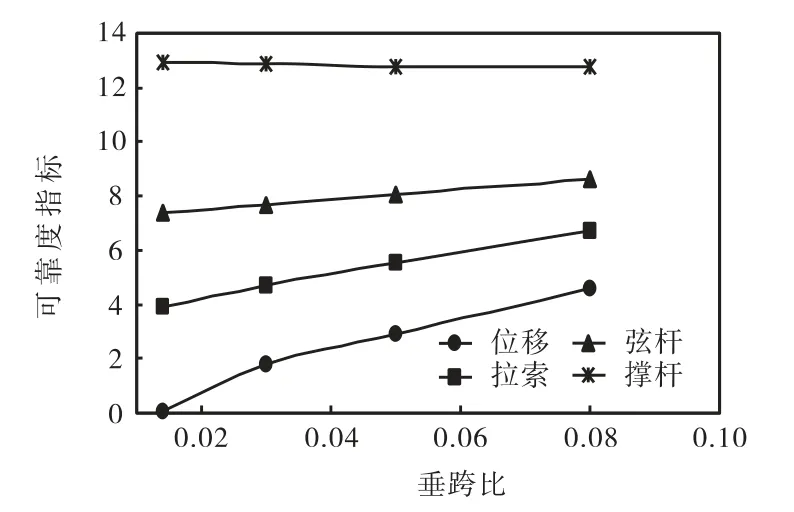
图8 垂跨比对结构可靠度的影响Fig.8 Influence of sag-span ratio on structure reliability

由图 8可知，随着垂跨比的增大，分别受拉索和弦杆承载力以及位移控制的结构可靠度指标均呈增大趋势，而撑杆承载力控制的结构可靠度指标则呈减小趋势．由以上变化规律可知，索对撑杆的约束作用在增大，而撑杆对上层筒壳的支撑作用也在增大，所以体系的弦支作用最终是在增大的，故结构受位移限值控制的可靠度会随着垂跨比的增大而逐渐增大．在对弦支筒壳结构进行设计时，垂跨比过小会使结构的弦支作用减弱，使得索力很大但作用效率很低，过大的垂跨比则会使索的内力变小，对抗震和抗风不利．在实际工程结构中，由于索垂跨比还受建筑净高的限制，因此一般取值较小．在满足建筑要求条件下，本文建议弦支筒壳结构垂跨比取值在 0.02～0.06为宜．

5.3 撑杆数目的影响

以弦支筒壳标准模型为基础，保持其他条件不变，只改变结构的撑杆数目，研究其对弦支筒壳结构可靠度的影响．本文将撑杆数目分别取为 3、5、7、9和 11五种情况进行了相应分析，此时可靠度指标随撑杆数变化的曲线见图9．

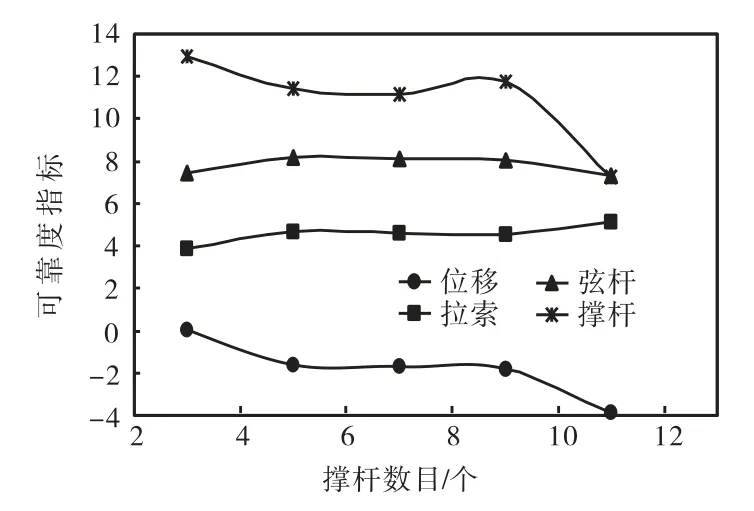
图9 撑杆数对结构可靠度的影响Fig.9 Influence of strut number on structure reliability

由图 9可知，随着撑杆数的增多，受位移控制的结构可靠度指标均呈减小趋势；拉索承载力控制的结构可靠度指标在撑杆为3时最小，撑杆为11时最大，当撑杆数在 5～9之间变化时，可靠度指标基本保持不变；撑杆承载力控制的可靠度指标则与拉索相反；随着撑杆数的增多，弦杆承载力控制的结构可靠度指标有一定程度的增加，但当撑杆数大于 9以后，又开始呈减小趋势．由以上变化规律可知，当撑杆数很少时，增加撑杆会在一定程度上增大弦杆的可靠度，但随着撑杆数的增加，这种效果不再明显且达到一定数目时又呈减小趋势；过多地增加撑杆还会使得结构的位移变大，结构可靠度降低，从而不满足《建筑结构可靠度设计统一标准》(GB 50068—2001)要求．所以，一般不将大幅度地增加撑杆数作为改善上弦筒壳受力的方法，且撑杆数在能满足要求的前提下以少设置为宜．

5.4 预应力作用对结构各失效模式的影响

拉索在施加预应力、承受外部荷载等方面起着关键作用．由于索的弹性模量和组成结构的刚性杆件大致接近，但强度却是杆件的5倍左右，所以，具体预应力控制在何种程度才能符合结构性能要求，需要进行研究和分析．取预应力的变化范围为标准模型中的0.6～1.4倍，随着结构预应力倍数的增加，受索、弦杆和撑杆承载力以及位移限值控制的可靠度指标如图 10所示，结构整体稳定性的可靠度指标如图 11所示．

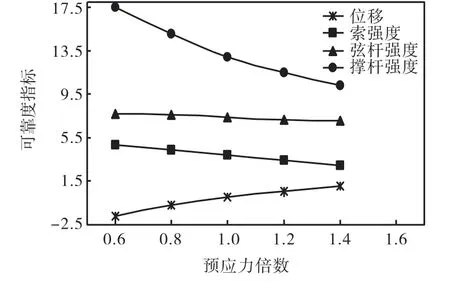
图10 预应力对结构可靠度的影响Fig.10 Influence of prestressing force on structure Fig.10 reliability

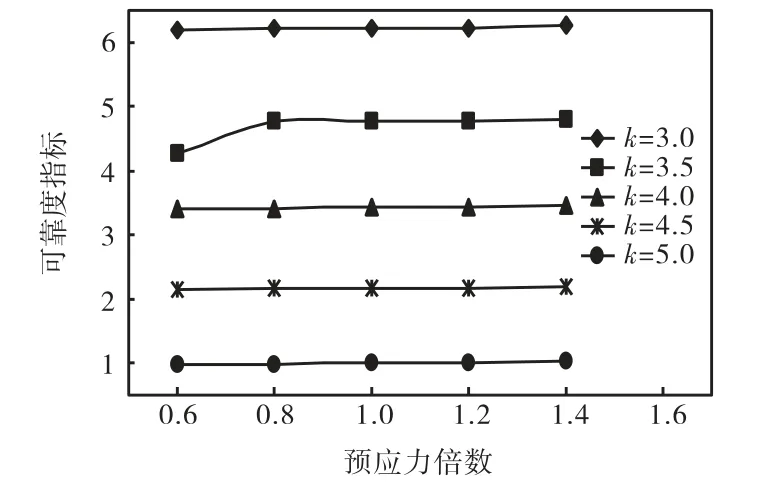
图11 预应力对结构稳定性可靠度的影响Fig.11 Influence of prestressing force on reliability of Fig.1 1 structure stability

由图 10可知，随着预应力倍数的增加，索、弦杆和撑杆承载力方面的可靠度指标呈减小趋势，而受位移控制的可靠度指标呈增大趋势．当预应力水平较低时，可靠度指标的增减幅度较大，随着预应力的增大，各可靠度指标变化趋向平缓．如拉索中的预应力取为标准模型中的0.6倍时，位移可靠指标为-1.71；当初始应变倍数为 1时，位移可靠度指标为 0.06，增加值为1.65．而当初始应变倍数从1.2提高至1.4时增加值仅为0.417 7．

由图 11可知，随着预应力倍数的增加，整体稳定性可靠度指标增幅很小，基本可以忽略不计，可见预应力取值大小对结构的稳定性影响不大．这是因为预应力的存在使结构具有初始几何刚度，从而影响结构的变形．但对于半刚性或是刚性结构，结构几何刚度占整个刚度的比例很小，它的改变对结构刚度影响不大，从理论上来讲预应力的大小对结构物理模型的刚度影响是微小的．

6 结 论

(1) 由计算结果可知，在弦支筒壳结构整体屈曲、承载力、变形3种失效模式下，受位移控制的可靠度最小，其次是整体稳定性和拉索承载力，弦杆和撑杆承载力相应的可靠度较大．

(2) 弦支筒壳的屈曲特征值、非线性屈曲临界荷载值和整体稳定性的可靠度指标均比单层筒壳大幅度提高，说明增加预应力拉索和撑杆将大大改善单层筒壳的稳定性．

(3) 随着矢跨比的增大，不同失效模式下的可靠度指标均呈增大趋势．矢跨比过小会使结构的刚度变小，截面设计过大而不经济；矢跨比过大会使拉索对上层筒壳的约束作用减弱，同时用钢量也会增大而不经济．本文建议矢跨比取值在0.08～0.12为宜．

(4) 随着垂跨比的增大，除撑杆外其他失效模式下的可靠度指标均呈增大趋势．垂跨比过小，会使结构的弦支作用减弱，造成索力虽然很大但使用效率很低；垂跨比过大则会使索的内力变小，对抗震和抗风不利，同时会使得室内净空太小．本文建议垂跨比取值在0.02～0.06为宜．

(5) 随着撑杆数的增加，各项可靠度指标增加效果不明显，并且过多地增加撑杆会使得结构的位移变大，可靠度降低．所以，一般不将大幅度增加撑杆数作为改善上弦筒壳受力的方法．

(6) 随着预应力倍数的增加，承载力失效模式下的可靠度指标呈减小趋势，位移失效模式下的可靠度指标呈增大趋势，故结构预应力设计需控制在适当的范围内．从计算结果可以看出，预应力取值大小对结构的稳定性影响不大，从理论上来讲预应力大小对结构物理模型的刚度影响也是微小的．预应力施加方案也是影响预应力钢结构可靠度的关键，其影响程度则有待进一步研究分析．

［1］Saitoh Masao，Okasa Akira. The role of string in hybrid string structure[J]. Engineering Structures，1999，21(8)：756-769.

［2］Chen Zhihua，Li Yang. Parameter analysis on stability of a suspendome[J].International Journal of Space Struc-ture，2005，20(2)：115-124.

［3］Wu Minger. Analytical method for the lateral buckling of the struts in beam string structures[J].Engineering Structures，2008，30(9)：2301-2310.

［4］Xue Weichen，Liu Sheng. Design optimization and experimental study on beam string structures[J].Journal ofConstructional Steel Research，2009，65(1)：70-80.

［5］陆赐麟，尹思明，刘锡良. 现代预应力钢结构[M]. 北京：人民交通出版社，2003.

Lu Cilin，Yin Siming，Liu Xiliang.Modern Prestressed Steel Structures[M]. Beijing：China Communications Press，2003(in Chinese).

［6］Jin Cheng，Li Q S. Application of the response surface methods to solve inverse reliability problems with implicit response functions[J].China Computational Mechanics，2009，43(4)：451-459.

［7］Nguyen Xuan Son，Sellier A，Duprat F，et al. Adaptive response surface method based on a double weighted regression technique[J].Probabilistic Engineering Mechanics，2009，24(2)：135-143.

［8］卢家森，张其林. 基于可靠度的单层网壳稳定设计方法[J]. 建筑结构学报，2006，27(6)：108-113.

Lu Jiasen，Zhang Qilin. Design method for latticed shells based on reliability theory[J]. Journal of Building Structures，2006，27(6)：108-113(in Chinese).

［9］张新培. 建筑结构可靠度分析与设计[M]. 北京：科学出版社，2001.

Zhang Xinpei.Reliability Analysis and Design of Building Structure[M]. Beijing：Science Press，2001(in Chinese).

［10］中国钢结构协会专家委员会. CECS 212—2006 预应力钢结构技术规程[S]. 北京：中国计划出版社，2006.

Expert Committee of China Steel Construction Society.CECS 212—2006 Technical Specification for Prestressed Steel Structures[S]. Beijing：China Planning Press，2006(in Chinese).

［11］沈世钊. 网壳结构的稳定性[J]. 土木工程学报，1999，32(6)：11-19.

Shen Shizhao. Stability of latticed shells[J].Civil Engineering Journal，1999，32(6)：11-19(in Chinese).

［12］Yu Fang，Zhang Qilin. Stability analysis of steel space structures with system parametric uncertainties[J].Communication in Numerical Methods in Engineering，2000，16(4)：267-273.