成层土地基在强夯作用下的孔压响应

闫澍旺，魏 芸

(天津大学建筑工程学院，天津 300072)

近年来有不少研究人员通过计算机仿真模拟强夯[1-8]，模拟方法普遍是将夯锤对土的冲击作用假定为在某一极短时间内按正弦或三角形规律变化的应力时程曲线作用在地基土上，这种方法的弊端是夯锤与地基土接触的时间及冲击作用力的峰值大小和变化规律均需按经验公式确定，且无法考虑锤体自身的质量．笔者以工程实测资料为基础，运用岩土工程专用有限差分软件 FLAC3D对强夯中的单点单次夯击过程进行了数值模拟，模拟过程突破传统，从强夯所导致的直观效果即形成某一深度的夯坑出发，研究地基土在瞬间冲击作用下的孔压响应．与实测资料的对比表明，这种模拟方法较为有效．此外，通过研究首次提出强夯法在处理包含饱和软土层在内的成层土地基时，存在所谓的“软土核”效应，并针对该工程提出了发生“软土核”效应的“临界软土层厚度”的概念．在固结分析中采用了考虑孔隙水压缩性的分析方法，并基于实测资料通过反分析获得不同土中孔隙水的体积压缩模量，验证了饱和软土中气泡含量比饱和砂土中气泡含量高的事实，其孔压分析结果更能反映地基土的真实情况．

1 数学模型的建立

数学模型的力学机制是通过几何方程、运动法则和本构方程以及流体连续性方程推导出来的．推导的结果是一系列由力学变量(应力)和运动学变量(应变率、速度)表示的偏微分方程，而后运用有限差分方法将偏微分方程转化成线性方程组，在给定几何模型、材料参数以及初始条件和边界条件时即可求解．

1.1 运动方程

在连续固体介质中，运动方程可概括为

式中：u为位移；u˙为速度．

1.2 几何方程

几何方程表述的是位移与应变之间的关系，将几何方程两边对时间求导即可得到用速度梯度表达的应变率，即

1.3 本构方程

本构方程选用岩土分析中参数简单且应用较广的莫尔-库仑(Mohr-Coulomb)本构关系，其破坏包络线由莫尔库仑的剪切屈服函数和拉应力屈服函数联合构成，与拉应力流动法则相关联而与剪切流动法则不相关联．

若h＞0，说明是拉坏；反之是剪切破坏．据此则可运用流动法则进行计算，将应力点回归到相应的破坏包络线上．

1.4 流体连续性方程

多孔介质中的流体本构方程用来描述孔压与饱和度、孔隙水体积、土体体应变和饱和度等变量之间的相互关系，即

式中：p为超静孔压；s为饱和度；ς为孔隙水体积；ε为土体体积应变；M 为比奥模数；n为孔隙率；α为比奥系数．

土体单元中的流体满足流体质量平衡方程，即土体中单位时间内流体体积的增加量应等于由于流体源的存在流进单元中的流体体积减去由于流体运动而流出单元中的流体体积

将式(2)、式(7)代入式(6)与式(1)组成方程组，通过对空间微分进行有限差分逼近和对时间导数进行有限差分近似，得到线性方程组，在给定的初始条件和边界条件下即可求解．

2 FLAC 3D模型的建立

2.1 工程概况及实测数据

海拉尔至满洲里一级公路是“五纵七横”国道主干线第一横——绥芬河至满洲里公路在内蒙境内的重要组成部分，主线全长190.985,km．其中K(543+300)～K(553+200)段(二卡段)位于呼伦贝尔草原二卡湿地鸟类自然保护区．湿地两端为海拉尔河及新开河，该段除局部段落地表水干枯植被减少外，其余路段地表为塔头、芦苇等喜水草类，其表层土质为草根、泥炭腐质土或淤泥质砂黏土，总厚度在 0.4～2.7,m左右，其下为粉细砂．该段有6,km路线穿越海拉尔河漫滩湿地，地表积水较严重，如图1所示．

图1 地表积水照片Fig.1 Photo of water in surface

设计提出用开山石混合料形成强夯置换墩的地基加固方案．在强夯施工过程中对夯坑下一定深度和一定范围内地基土的孔隙水压力变化进行了监测．图 2为实际工程中孔压计埋设深度及土层分布情况(图中尺寸单位为 cm，是指距地表碎石上表层的距离)．实测孔压响应曲线如图3和图4所示．

图2 孔压计实际埋设位置Fig.2 Actual positions of piezometers

图3 砂土中的实测超静孔压Fig.3 Observed excess pore pressure in sand

表1 土层分布及各层物理力学参数Tab.1 Soil stratum and physical mechanics parameters of each layer

图4 淤泥中的实测超静孔压Fig.4 Observed excess pore pressure in clay

砂土层和软黏土层中超静孔压时程响应曲线呈现出各自不同的特点．砂土中超静孔压上升到峰值所需的时间比软土中超静孔压达到峰值所需的时间短，且砂土中超静孔压峰值小于饱和软土中的超静孔压峰值．就这一现象产生的原因，运用数值手段进行了分析．

2.2 基本假定

如图2所示地基土层分布不均匀，地表开山碎石层厚度在 190～200,cm 之间，试验段淤泥层厚度在20～60,cm 之间．建立数值模型时在各土层厚度上做了一些简化，如图5所示．此外，还做了如下假定：

(1)各层土体均为各向同性弹塑性体；

(2)夯锤为线弹性体；

(3)计算过程中，土体及夯锤的物理力学参数保持不变；

(4)流体流动符合达西定律，且各方向渗透系数相同；

(5)土颗粒不可压缩(即取比奥系数1=α)．

2.3 本构模型的选择

土体采用 Mohr-Coulomb模型，夯锤用各向同性弹性模型．

2.4 土体及夯锤参数选择

土体分层如图 2所示，共分 4层，由上到下分别为厚2,m的碎石层、0.5,m厚的淤泥土、1.0,m厚的细砂层和16.5,m厚的边界土层．各土体参数见表 1，夯锤参数见表2．

表2 夯锤物理力学参数Tab.2 Hammer physical mechanics parameters

2.5 加载过程

实测资料表明，夯坑的平均深度为 0.5,m，因此，加载方式是在流固耦合模块中，通过给夯锤一恒速(0.002,m/步)，使其在很少的计算步内(250,步)完成0.5,m的位移(此过程较短暂，认为是不排水过程)，之后，将锤体的速度初始化为零，进行流固耦合分析．实际证明这种加载方式能够直观反映强夯的夯击过程以及夯后土体的固结过程．

2.6 模型的建立

(1)模型大小：24,m×24,m×20,m，夯锤的作用位置在模型的正中上表面处；

(2)单元类型选择：土体用 Radcylinder单元，靠近夯锤的地方网格较密．夯锤采用Cylinder单元；

(3)夯锤与土体的接触：假定接触面光滑，即夯锤只有竖向位移．

2.7 边界条件

(1)固体边界：模型四周及下边界都采用位移边界，分别固定其相应法线方向的位移；

距离不二越展台不远处是福伊特公司的展台。在这家德国家族企业的展台上，摆放着四台艾米卡机器人，其中一台正演示着如何自动完成芯片检测。作为福伊特新近纳入版图的业务，艾米卡机器人有着能与人类同台合作的特点，该类型产品被称为协作机器人。今年4月，福伊特与艾米卡机器人成立了合资公司福伊特机器人公司，共同开拓新市场，首要目标就指向了中国。此次进博会是福伊特机器人产品在中国亮相的第三场展会。福伊特机器人公司首席销售官托尔斯滕·弗里德里希称，公司在中国将主要针对电子行业等领域的客户，因为这里是全球最重要的电子产品生产国。

(2)流体边界：除上表面是可渗透边界之外，其余边界均为不可渗透边界．

3 计算过程结果

3.1 计算模型的网格划分

图5是三维数值模型网格划分的剖面图，根据分析的需要靠近夯锤位置网格划分密度较大．

图5 网格剖分(单位：米)Fig.5 Mesh grid(unit:m)

3.2 计算过程

由式(4)可见，超静孔压的变化率与比奥模数 M成正比，而比奥模数又与孔隙水的体积压缩模量成正比．工程地处湿地，土中有机物含量较高，决定了土中气泡含量较大，而气泡含量的多少又直接影响孔隙水的压缩性．基于实测资料，通过反分析法得到该地区淤泥和细砂中孔隙水的体积压缩模量分别为0.13,MPa和 0.51,MPa，验证了淤泥的孔隙水中所含气泡含量大于渗透性较好的细砂的孔隙水中所含气泡含量．

(1)初始地应力平衡：该阶段假定各层土都是正常固结土．

(2)在地表下 0.5,m 处加地下水位(原地表积水上加 2.0,m厚的碎石垫层后作为数值模型中的地表，即z轴零点)，形成初始孔压场．

(3)加夯锤并让夯锤在 250,步之内形成一瞬时位移0.5,m，该过程认为土体不排水，之后进行土体与水的流固耦合分析．

3.3 计算结果分析

通过在不同土层不同位置处设置孔压监测点，得到不同土层中某一点在夯击过程中的超静孔压响应．以夯锤底中心位置为坐标原点，向右为 x轴正向，向上为 z轴正向，则图 6所示曲线的观测点位于淤泥层中，坐标为(2.8，1.4，-2.25)，图 7所示曲线的观测点在细砂层中，坐标为(2.8，0，-2.75)．图中 p指超静孔压，t指时间．

图 6和图 7中曲线表示地基土在受到冲击荷载作用时某一点的超静孔压时程曲线的实测值与计算值的对比．可以看出，在夯击过程中，淤泥层中的超静孔压上升速度较慢，在 50,s左右才达到最大值；而细砂中的超静孔压则上升较快，在 2,s左右达到峰值．实测数据与计算结果均表明在冲击荷载作用下淤泥土中超静孔压值比渗透性大的砂土中的超静孔压值大．

图6 淤泥层中的p-t曲线Fig.6 p-t curve in clay

图7 细砂中的p-t曲线Fig.7 p-t curve in sand

图 8为夯锤中心点以下不同深度处的超静孔压所能达到的峰值 pmax与该点距地表距离 h的关系曲线．在同一种土中，超静孔压峰值的大小可以反映冲击波传到该处剩余能量的大小．图 9是夯锤中心点以下不同深度处超静孔压达到峰值所需的时间 t与该点距地表距离h的关系曲线，它反映波能量在土体中沿纵向的衰减过程．由于实测资料中孔压观测点距夯点的距离普遍在 8,m 以外，超静孔压值很小，对该处的分析没有参考价值，因此图中只有计算值．

图8 夯锤中心点下的p-h曲线Fig.8 p-h curve under center of hammer

图9 夯锤中心点下的t-h曲线Fig.9 t-h curve under center of hammer

从图8可以看出，超静孔压峰值在8.4,m处下降到1,kPa左右，8.4,m以下的超静孔压峰值都在1,kPa以下，可以认为其有效影响深度达到了8.4,m．从图9可以看出随着深度的增加，超静孔压达到峰值所需时间加长，且随深度减小，可以体现波在土体中的传播和波能量的衰减过程．

同理，通过跟踪监测同一土层中同一深度范围内超静孔压的响应情况可以体现冲击波能量在径向的传播和衰减过程，如图 10和图 11所示(d指距离夯锤中心点以下某处的横向距离).

图10 深度3.0 m处的p-d曲线Fig.10 p-d curve at depth of 3.0 m

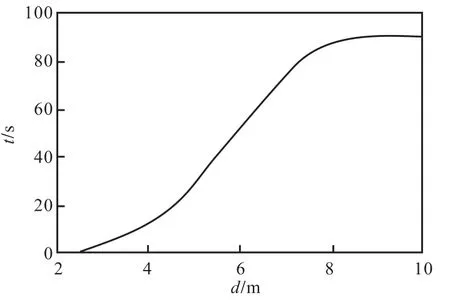
图11 埋深3.0 m处t-d曲线Fig.11 t-d curve at depth of 3.0.m

从图 10可以看出，超静孔压峰值在径向 7.3,m处下降到 1,kPa左右，7.3,m以外的孔压峰值都在1,kPa以下，可认为其径向有效影响范围达到了7.3,m．从图 11可以看出随着离夯锤距离的增加，超静孔压达到峰值所需时间加长，孔压峰值越来越小，可以体现波在土体中沿横向的传播过程．

从图 9和图 11还可看出，波的能量在竖向比在径向传播快，例如 50,s时，波在竖向的传播距离已经到达 8.4,m，而径向才到达 5.4,m，即波是以长轴在竖直方向的椭球体形状向外传播的．

图 12为稳定状态下的位移图，右侧为位移云图中的图例，单位为m．

从图 12的竖向位移云图分布看到，锤体最大竖向位移也即夯坑最大深度可达 68,cm，坑边最大隆起8.2,cm，说明强夯的大部分能量消耗在对土体体积的压缩上．

图 13为地基土中最大主应力分布云图，“-”代表压应力．

图12 竖向位移Fig.12 Distribution of z-displacement

图13 最大主应力分布Fig.13 Maximum principal stress distribution contour

从图 13可以看出土体中最大主应力在地表下5,m之内变化梯度比较大，说明5,m内是强夯作用的主要影响区，径向最大主应力变化梯度比较大的区域在 3.0,m范围之内，证明该区域之内是强夯的主要影响区．本工程在实际施工中采取两遍夯击，第一遍夯点布置为间距 5.6,m的正方形，第二遍在正方形中心处夯击，这样既有利于孔压的消散又能够保证整个地基土得到加固．

对均质土而言，离夯锤竖向距离越大，土中产生的超静孔压越小，在其他条件一定的情况下，淤泥中所产生的超静孔压要大于其他渗透性较大的土，而一旦超过了某厚度，这种特点将不存在．图 14为淤泥层厚度不同时的孔压分布云图．

从图 14可见，当淤泥层厚度为 0.5,m时“软土核”效应最为明显(见图 14(a))；到 1.5,m 时已经有所减弱(见图 14(b))；当软土层厚度增加到 3.5,m 时这种现象基本消失(见图 14(c))．可见对于本文的分析模型，强夯能够对软土层起到加固作用的临界软土层厚度为3.5,m以内．

图14 淤泥层厚度H不同时的孔压分布Fig.14 Pore pressure distribution contours for different silt depth H

4 结 论

实践中，强夯法加固饱和软土有时会出现“橡皮土”现象，这是因为即使冲击能量使得软土中的孔隙水在瞬间得以析出，如果没有良好的排水通道，在夯击作用结束后，排出的大部分水分又会随着软土的触变恢复回到软土中，导致夯击能量的浪费．因此，强夯法加固饱和软土的内在机理在于夯锤的冲击能量能否使得软土与其相邻土层之间形成较大的超静孔压梯度，以及软土中排出的水分能否迅速得到消散，从而有效加速软土的固结．“软土层临界厚度”正是基于这样的认识而提出的，它是一个与夯击能量、土层之间渗透性差异大小以及软土层所分布的深度等相关的量．它的进一步研究可以使强夯法更有效地运用于饱和软土的加固．

(1)通过模拟夯锤瞬时位移的方法替代传统施加动荷载的方法来模拟强夯的加固效果，过程明确，实现方法简单，且与实测资料的对比证明这种模拟方法较为有效．

(2)在成层土地基中，若软土层相邻土层渗透性较好，则强夯产生的超静孔压在地基中分布呈“核”型，产生“软土核”效应，正是这种效应增大了软土与周围土的孔压梯度，从而加速了软土的固结．

(3)软土孔隙水中气泡含量较高，大大增加了软土中孔隙水的压缩性，导致在相同压力作用下，饱和软土所产生的体应变较大．在不排水状态下，这种体积上的压缩只能通过气泡的压缩(将其折算到孔隙水的压缩上)来实现，这样，孔隙水所占的体积的变化量较大，孔压的改变量也相应较大，这就是饱和软土中产生的超静孔压比周围渗透性较大土中所产生超静孔压大的内在原因，也是“软土核”效应即对软土固结起到加速作用的根源所在．

(4)强夯作用要在成层土地基中产生“软土核”效应，软土层厚度必须小于“软土层临界厚度”，否则采用强夯法也就达不到加固软土地基的目的．

［1］蔡袁强，陈仁伟，徐长节. 强夯加固机理的大变形数值分析[J]. 浙江大学学报：工学版，2005，39(1)：65-69.

Cai Yuanqiang，Chen Renwei，Xu Changjie. Numerical analysis of dynamic compaction using large deformation theory [J].Journal of Zhejiang University：Engineering Science， 2005，39(1)：65-69(in Chinese).

［2］王桂尧，胡振南，匡希龙. 红砂岩路基强夯处理大变形数值模拟方法与效果分析[J]. 岩土力学，2008，29(9)：2451-2456.

Wang Guiyao，Hu Zhennan，Kuang Xilong. Largestrain numerical simulation and experimental research about improving red-sandstone embankment by dynamic compaction [J].Rock and Soil Mechanics，2008，29(9)：2451-2456(in Chinese).

［3］孟庆山，汪 稔. 软土动力固结理论研究及应用的现状[J]. 建筑技术，2005，36(3)：179-182.

Meng Qinshan，Wang Ren. The present situation of research and application of dynamic consolidation theory of soft soil [J].Architecture Technology，2005，36(3)：179-182(in Chinese).

［4］秦小勇，李晓杰，Dik Voerman，等. 基于 LS-DYNA强夯冲击数值模拟[J]. 水运工程，2007，407(9)：31-35．

Qin Xiaoyong，Li Xiaojie，Dik Voerman，et al. Numerical modeling of dynamic consolidation using LSDYNA [J].Port and Waterway Engineering，2007，407(9)：31-35(in Chinese).

［5］王继果，王永增，周 峰，等. 强夯法处理软弱地基的数值模拟[J]. 工程建设与设计，2006(1)：37-39．

Wang Jiguo，Wang Yongzeng，Zhou Feng，et al. Digital simulation of dynamic compaction in ground improvement[J].Engineering Construction and Design，2006(1)：37-39(in Chinese).

［6］蒋 鹏，李荣强，孔德坊. 强夯大变形冲击碰撞数值分析[J]. 岩土工程学报，2000，22(2)：222-226.

Jiang Peng，Li Rongqiang，Kong Defang. Numerical analysis of large deformation impact and collision properties during dynamic compaction[J]. Chinese Journal of Geotechnical Engineering，2000，22(2)：222-226(in Chinese).

［7］蔡袁强，陈 超，徐长节. 强夯加固回填土地基的三维数值模拟[J]. 岩土力学，2007，28(6)：1108-1112.

Cai Yuanqiang，Chen Chao，Xu Changjie. Threedimensional numerical simulation of dynamic compaction of backfilled soil [J].Rock and Soil Mechanics，2007，28(6)：1108-1112(in Chinese).

［8］孔令伟，袁建新. 强夯时地基土的应力场分布特征及其应用[J]. 岩土力学，1999，20(3)：513-527.

Kong Lingwei，Yuan Jianxin. Stress field distribution characteristics of foundation during dynamic consolidation and its application[J].Rock and Soil Mechanics，1999，20(3)：513-527(in Chinese).