基于异频相位处理的高精度频率测量系统

杜保强，周 渭

(1. 西安电子科技大学信息处理研究所，西安 710071；2. 河南职业技术学院信息工程系，郑州 450046)

随着航空航天、激光测距、精密定位、粒子飞行探测及其他高科技领域的技术发展，对频率尤其是高频率点频信号的测量精度提出了更高要求．目前，常用的频率测量方法有直接计数法、多周期同步法、模拟内插法和游标法等[1-2]．直接计数法和多周期同步法存在±1个计数误差，由于填充信号频率值一般小于109Hz，所以，频率测量精度差小于10-9, s-1．采用这种方法设计的频率计，结构简单，成本低廉，但精度差；模拟内插法仍存在±1个计数误差，但采用内插器使±1个计数误差减小到 1/1 000左右，使测量精度达到10-11s-1量级；游标法类似模拟内插法，采用游标振荡器使±1个计数误差减小到 1/1,000左右，测量精度也能达到 10-11, s-1量级；采用这两种方法实现的仪器，精度很高，但明显的电路设计复杂度和昂贵的造价限制了其应用．文献[3-4]相检宽带测频技术有效地降低了频率测量中存在的±1个计数误差，使测量精度达到 10-10, s-1量级，但相位重合点的不唯一性和随机性，很难使其精度再进一步提高．针对以上测量方法的优缺点，笔者提出了一种基于异频相位处理的新型高精度频率测量方案．新方案利用信号间的频率关系及相位差周期性变化的规律性与 FPGA片上技术相结合，不仅巧妙地解决了相检宽带测频技术中存在的问题，而且还简化了电路结构，降低了成本，同时也提高了系统的稳定性．

1 测量原理

正是由于两频率信号之间的相互关系和它们之间的量化相移分辨率，导致了两频率信号之间不断出现相位重合，而且在一些相位重合处有可能出现同步．如果此时在两相位重合处建立测量闸门，就能克服在传统频率测量中存在的±1个计数误差，进而提高测量精度．系统原理框图如图1所示．

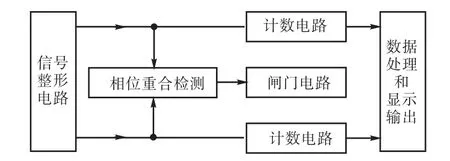
图1 异频相位重合检测原理Fig.1 Different frequency phase coincidence detection

2 设计方案

根据异频相位重合检测理论，测量精度的提高，关键在于异频相位重合检测电路对相位重合点尤其是最佳相位重合点捕捉的程度．所谓相位重合点并非绝对重合，由于受电子器件分辨率的限制，捕捉到的相位重合点不是一个窄脉冲而是一簇窄脉冲，而且量化相移分辨率越高，簇中窄脉冲的个数就越多．在这一簇窄脉冲中，幅度最高的为最佳相位重合点，其他称为虚假相位重合点[9]．窄脉冲在相位重合处的出现是随机的，它们对计数闸门(即测量闸门)的触发也是随机的，这样两相位重合点之间的时间间隔就存在很大的不确定性，严重地影响了测量精度．为了进一步提高测量精度，必须减少簇中窄脉冲的个数以达到有效捕捉最佳相位重合点，降低对计数闸门触发的随机性．

2.1 脉宽调整电路

图2为具有延时可调的异频相位重合检测电路，其工作波形如图3所示．

图2 具有延时可调的异频相位重合检测电路Fig.2 Different frequency phase coincidence detection circuit with adjustable delay time

图3 异频相位重合检测工作波形Fig.3 Work waveform of different frequency phase coincidence detection

在这 Ne个有效脉冲中，如果取第k个有效脉冲来触发产生计数器的开门和关门信号，闸门误差最终表现为计数误差

式中：Nx是被测信号fx在计数闸门内的计数值；ΔNx是最大计数误差，ΔNx是由电路噪声引起的触发闸门脉冲在各自脉冲簇中的位置的差异Δk产生的．则

由式(9)可知，频率测量误差最终仅由Δk决定．显然，相位重合点中的有效脉冲数Ne越小Δk也就越小．根据式(7)，只要有效地控制延迟单元的延迟量td，使其略大于2tr，则可减少Ne，从而减小Δk．因此，在具体实现上，只要合理调整图 2电路中 f0P和fxP的脉冲宽度，即可达到减少 Ne的目的．在这种情况下，如果对于确定的被测信号 fx，再选用合适的频标 f0，合理地增大 Δ T ，则会极大地提高测量精度．

通过图2中可调延时单元对延时量的细调，从而改变 f0p和 fxP的脉冲宽度．这里对延时量的细调主要采用分压延时的办法，其原理及波形如图4所示．

图4 分压延时原理Fig.4 Bleeder delay principle

tde是利用分压延迟法引入的延时量，通过改变电位器上下部分的电阻比例，即可方便地调节延时量tde，由图4可知

tr是输入波形的上升时间，在本系统中 tr约为2,ns，所以 tde最大可到 1,ns．用这种方法来获得延时，延时量调节的分辨率可以到达 1,ps，而且获得的延时很稳定，重合点捕捉电路内延迟单元的总延时量为

式中 tdi是图2脉冲电路中延时单元的固定延时量，使其略小于 2 tr，再通过细调 tde使总延时量 td略大于2tr，则可大大减少相位重合脉冲中的有效脉冲数Ne，从而减小Δk，最终提高测量精度．

2.2 最佳相位重合点捕捉电路

经过脉宽调整电路后，有效脉冲的个数 Ne大大减少了，在这种情况下，系统的测量精度已达到很高，但是相对确定，若不采取其他措施，测量精度不可能再进一步提高．根据上面的分析，经图2电路后 Ne的分布仍然是正态分布，这种分布的特点是窄脉冲在最佳相位重合点两侧左右随机游动[11]．若此时在图 2电路的基础上增加一个相位重合控制电路，使标频信号 f0始终超前于被测量信号 fx，这样有效脉冲的个数在原来 Ne的基础上又少了一半，更加逼近最佳相位重合点，测量精度会更高．如图5所示．这里采用了一个边沿型 D触发器和一个反相器相结合作为相位重合控制电路．至此，有效脉冲的个数 Ne达到了最小的极限状态，计数闸门动作的随机性达到了最低，测量误差达到了最小，测量精度得到了大幅度地提高．

图5 最佳相位重合点捕捉电路Fig.5 Capture circuit of optimal phase coincidences

2.3 基于FPGA的系统实现

处于对系统测量速度、功耗、体积、成本及可靠性方面的考虑，系统在具体实现上采用了FPGA集成电路，即将逻辑电路全部集中在现场可编程门阵列(FPGA)芯片上，使其各部分达到最佳优越性能[12]．基于 FPGA的系统实现框图如图 6所示．标频信号和被测信号经整形后被送往 FPGA，整形电路部分对频率信号进行驱动和电平匹配，这部分是模拟电路，特别注意了实际电路的印刷电路版布局、布线、电源噪声及模拟和数据的耦合等问题．FPGA完成频率的测量．多点控制单元(MCU)从 FPGA中采集数据并进行处理，最后计算出被测频率信号的值，在液晶显示器(LCD)上显示出来．而人机接口部分用于设置系统的闸门、频率标称值等参数．

图6 系统实现Fig.6 System implementation

3 实验结果及分析

目前，基于FPGA技术的频率测量系统已研制出样机，频率测量范围为0.1～230,MHz，测量速度即达到频率稳定的时间约为30,s，频率稳定度可达到10-13, s-1量级．

3.1 系统自校

在基于FPGA的频率测量系统自校实验中，为了更好地捕捉到相位重合点，这里使用了 1台HP8662A 频率合成器．外频标为 10,MHz，由HP8662A频率合成器锁定，用此频标通过调节HP8662A频率合成器给出被测频率信号，由此得到不同的自校测试结果，如表1所示．

表1 系统自校测试结果Tab.1 System self-calibration text results

3.2 测频实验

为了验证样机实际的频率测量精度，这里使用了 OSA公司生产的超高稳定度 86,075,MHz OCXO(精度为 10-13s-1量级)作为频率合成器 HP8662A的频标信号，合成输出 10.000,010,MHz作为本系统的f0，用另外一组8607的OCXO和HP8662A产生被测频率 fx，测试数据如表2所示．

表2中的数据表明，本系统在测量与频标关系比较复杂的被测信号时测量精度也能达到 1 0-12s-1，而对于与频标关系较简单的被测信号，如常用的5,MHz、10,MHz等，其测量精度可达 1 0-13s-1．这与传统的XDU-17(理论精度 1 0-11s-1)频率测量仪相比，其测量精度有了很大程度的提高．

表2 频率测量实验结果Tab.2 Frequency measurement experiment results

根据上述实验结果，系统的自校精度很高而实际测量精度最高却只能达到 1 0-13s-1量级．这主要由于在不同源频率比对下HP8662A频率合成器噪声的影响和相位检测电路工作频率的限制造成的．在实际应用中，通过改善比对设备性能和使用一定频偏的高精度标准源，实际比对精度一般能够达到 1 0-13s-1量级，在某些频点上有可能会更高．

4 结 语

提出的基于异频相位处理的高精度频率测量系统的设计方案不再是利用传统的比相方法单纯依靠线路上的改进或微电子器件的发展来提高测量精度，而是利用自然界中周期性信号相互间的固有关系及变化规律，把这些规律应用于频率信号相互关系的处理中，无须频率归一化也可完成相互间的相位比对及处理．根据异频信号间实际相位重合点的分布规律，通过脉宽调整电路减少相位重合点的个数并在相位重合控制电路的帮助下有效地捕捉最佳相位重合点，进而降低测量闸门开启和关闭的随机性，实验结果表明，频率稳定度可达到 1 0-13s-1量级．与传统频率测量系统相比，新方案具有测量精度高、电路结构简单、成本低及系统稳定性高的优点．随着微电子工艺的发展和FPGA性能的提高，这种新型频率测量系统的测量精度有可能会进一步提高．

［1］Kalisz J，Pawlowski M，Pelka R. Error analysis and design of the Nutt time-interval digitiser with picosecond resolution[J].J Phys E：Sci Instrum，1987，20 (11)：1330-1341.

［2］Jansson J-P，Mantyniemi A，Kostamovaara J，et al. A CMOS time-to-digital converter with better than 10.ps single-shot precision[J].IEEE Journal of Solid-State Circuit，2006，41(6)：1286-1296.

［3］Zhou Wei，Xuang Zongqiang，Yu Jianguo. A novel frequency measurement method suitable for a large frequency ratio condition[J]. Chinese Physics Letters，Los Angeles，DSA，2004，21(5)：786-788.

［4］Wang Fengwei，Zhou Wei，Li Lin. A technique of ultra high frequency measurement[C]// Proceedings of the 2007International Frequency Control Symposium．Los Angeles，USA，2007：820-822.

［5］Zhou Wei，Zhou Hui，Fan Wenjing，et al． Equivalent phase comparison frequency and its characteristics[C]//Proceedings of the 2008 IEEE Frequency Control Symposium．Los Angeles，USA，2008：468-470.

［6］Du Baoqiang，Zhou Wei，Dong Shaofeng，et al.Group-period phase comparison method based on equivalent phase comparison frequency[J].Chinese Physics Letter，2009，26(7)：602-605.

［7］Zhou Hui. A time and frequency measurement technique based on length vernier [C]// Proceedings of the 2006IEEE International Frequency Control Symposium.Los Angeles，USA，2006：267-272.

［8］Zhou Wei. A novel frequency measurement method suitable for a large frequency ratio condition[J]. Chinese Physics Letters，2004，21(5)：786-788.

［9］杜保强，周 渭，陈法喜，等. 一种新型超高精度频标比对系统的设计[J]. 仪器仪表学报，2009，30(5)：967-972.

Du Baoqiang，Zhou Wei，Chen Faxi，et al. Design for novel ultra-high precision frequency standard comparison system[J].Chinese Journal of Scientific Instrument，2009，30(5)：967-972(in Chinese).

［10］王 海，周 渭. 高精度频率测量技术及实现[J]. 系统工程与电子技术，2008，30(5)：981-983.Wang Hai，Zhou Wei. High-accuracy frequency measurement scheme and its implementation[J].System Engineering and Electronics，2008，30(5)：981-983.

［11］屈八一，周 渭，秦红波，等. 基于双频信号相位重合点的秒信号产生法[J]. 西安电子科技大学学报，2008，35(5)：899-902，931.

Qu Bayi，Zhou Wei，Qin Hongbo，et al. Method for obtaining a second signal based on the phase coincidence sign between two frequency signals[J].Journal of Xidian University，2008，35(5)：899-902，931(in Chinese).

［12］黄志君，潘 攀，赖振华. 基于FPGA的多用信号源的设计与实现[J]. 天津大学学报，2006(增刊)：383-387.

Huang Zhijun，Pan Pan，Lai Zhenhua. Design and implementation of multiple signal source based on FPGA[J]. Journal of Tianjin University，2006 (Supp1)：383-387 (in Chinese).