硅基环形电-光调制器的理论分析和性能优化

张 彬，毛陆虹，谢 生，郭维廉，陈 燕，于 欣，张世林

(天津大学电子信息工程学院，天津 300072)

硅基光电子学的主要目标在于探求在同一硅衬底上集成光学和电学元件，其性能将优于单独的光学元件和电学元件．应用于 1.3～1.55 μm 波段光纤通信的硅基光电子学是一个非常有前途的研究领域[1]．但是，硅材料的一些特性，如间接带隙、低载流子迁移率等限制了其光学和电学性能，所以当今的光电集成回路(optics electronic integrated circuit，OEIC)技术主要利用三五族化合物半导体作为原材料．尽管如此，研究表明波长大于 1.2,μm的红外光可以在硅片上传导、探测、调制，具有低成本、便于集成的优点[2]．

由于硅本身的光电效应较弱，它对折射率的改变较小，所以需要较大的尺度以实现光电调制．Intel基于氧化金属半导体(metal oxide semiconductor，MOS结构研制了硅基高速调制器[3]，可以达到1,GHz的工作频率，这一成果具有很重要的意义．但是由于载流子浓度和光学折射率之间的耦合关系较弱，所以仍然需要较长的调制长度．为了克服这一缺点，学者们提出了各种新型的结构，其中环形谐振器结构是一种较为新颖的设计．环形光学谐振结构可以有效地增强折射率变化对传输特性的影响，它最早应用于光纤领域，Xu等[4]首次将这种设想应用在硅基光调制器．

通过调节环形结构的有效折射率，改变等效环形光程，可以获得较大的光强的衰减．使用 PIN型结构可以有效地改变载流子的浓度，进而改变有效光折射率进行调制．从文献[4]的实验结果观察到了谐振波长随着外加偏压大小的变化，而且谐振峰值随着外加电压增加的变化显著，作者将这种变化归结为载流子浓度增加所引发的光吸收的增强．通常，PIN结构被认为正向调制速度较低[5]，但是从文献[4]中的结果看，针对单极性归零码(return to zero，RZ)编码的信号调制器的调制深度可以达到 1.5,Gb/s的水平，远远高于通常PIN结构调制器的调制速度，这说明光学谐振特性对提高光调制器的调制速度有非常重要的作用．所以研究光学谐振特性和系统整体调制速度之间的相互关系很有必要，可以找出调制速度提高的根本原因．

为了研究光学谐振特性和系统整体调制速度之间的相互关系，笔者对环行谐振腔调制器的电学和光学特性建立了相应数学模型，并推导了调制速度的解析表达式，对器件机理研究和性能优化有重要的意义．

1 硅基环形电-光调制器的理论分析

环形PIN电-光调制器的结构如图1所示．

图1 环形PIN电-光调制器的结构Fig.1 Structure of ring PIN electro-optic modulator

由于注入电荷的变化引发环形谐振器载流子浓度的变化，从而引发谐振峰值的变化．其结果是等效光程在谐振处变化为0，即

式中ω0、n0和q0分别为谐振处的角频率、透过率和PIN结处存储的电荷量，因此有

在正向电压的驱动下， 电荷的上升过程由下面的微分方程决定．

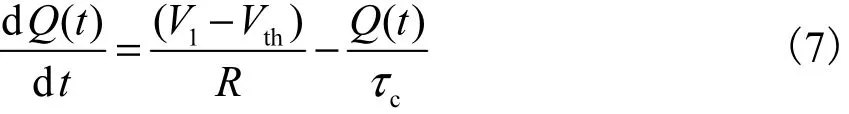
式中 Vth为阈值电压，Vth= 0 .7 V ．求解此方程得

式中：τc为载流子的寿命； R为负载电阻．从式(4)可以看到只要q＞3q0，光透过率T′＞90%，因此对结充电到 3q0的时间是光的上升时间，它将小于电荷的上升时间．如果 3q0远小于电荷的稳态数值，则系统的上升时间将被大大缩小．

在反向电压的驱动下，电荷的下降过程则由下面的微分方程决定．

面对日益严峻的大数据安全形势，目前主流的安全解决方法包括：经典的文件访问控制技术、设备加密技术、匿名保护技术、加密保护技术、数据水印技术等。同时提出利用大数据技术本身用作大数据安全防护的实现方法，增强大数据时代的信息安全防护性能。

式中 Cj为结电容，从式(10)可以看到当电荷下降到3q0之前，光透过率几乎保持不变． 然后开始下降直到电荷下降到q，光透过率下降到 10%，表示下降0过程结束．综上所述，微环电光调制器的电荷延时主要由4部分组成．

(1)电荷上升到 3 q0的延时为

(2)电荷上升至03q时刻，到脉冲下降沿的延时为

式中 T表示脉冲的总长度．(1)、(2)两个过程积累的总电荷为

(3)脉冲下降沿到电荷下降至 3q0所需的延时为

(4) 电荷由 3q0下降至1/3 q0所需要的延时为

对于光信号而言，延时主要是由其中的(1)、(3)、(4)3部分组成，所以总的延时可以表达为

从式(16)可知总的延时是Q的函数．

设基本参数为表1所示．

表1 式(16)中的基本物理参数定义Tab.1 Values of parameters in Eq.(16)

从图2中可以看到不是Q值越高，延时越短，这是由于总延时是由上升时间和下降时间之和确定的，由于电荷和光强之间的非线性关系，由式(4)可以看出，电荷量只需达到 3 q0，就可以使得光强达到90%的稳态数值，提高 Q值可以减少 q0的数值因而能减少上升时间，但下降过程也会因 q0的减少而进一步的增加．从图2中可以看出当 Q =1× 1 03.3时延时存在极大值，随着 Q 值的进一步增加，延时减少，这是由于上升时间减少的影响大于下降时间的增加所致．

图2 Q值和系统延时之间的关系Fig.2 Relationship between Q and system delay time

2 提高环形电-光调制器调制速度的方法

2.1 采用预增强的输入脉冲

从分析可以看到，电荷上升和下降延时的4部分时间里，除第二部分延时外都将出现在输出光信号的延时中，如果当电荷达到 3 q0后，突然降低电压数值使其电荷达到并维持稳态数值 3 q0，则可以消除第三部分的延时，从而使总的延时进一步的缩小．文献[8]的实验证明此方法可有效地减少环形电光调制器的调制速度．

采用预增强输入脉冲的延时和 Q值的关系如图2中实线所示．从图 2中可以看到，采用了预增强的输入脉冲后，当 Q值大于 10,000以后，延时随 Q值的增强更迅速减少；使用增强输入脉冲后调制速度可大于10,GHz．

2.2 减少波导宽度

从式(18)可以看出减少波导宽度可以减少结体积，从而减少 q0提高调制速度．但另一方面，光波导必须满足单模的工作条件．

系统必须满足单模传输条件[9]，即

式中：t=W/H；r= h/H．图3表示波导的单模特性曲线，不难得到，当满足 W=H 时，必须保证 0.5,〈 r,〈,0.58,最大绝对误差应该控制在 0.08W，所以在 H或者 W非常小的条件下，需要满足上面的约束关系，将对刻蚀工艺提出较高的精度要求，这就决定了这种方法具有一定的局限性．

图3 脊型波导的单模特性曲线Fig.3 Single mode characteristic curve of rib waveguide

2.3 增加环半径和减少耦合系数

文献[10]指出决定环形谐振器Q值的表达式为

式中：L为环路的周长；neff为脊型波导的有效折射率；κ为耦合系数；c为真空中的光波波长．图 4表示了耦合系数和系统 Q值的关系．从(19)可知提高 Q值的两种方法：①增加环半径，从而增加环周长 L，但如果环周长过长，光环绕一周，光强衰减到 0，则环无法起到光增益的作用，从而限制了 Q值的提高；②减少耦合系数，与耦合系数直接相关的是直波导和环形波导之间的间隔和耦合的长度．使用光学仿真软件可以定量地得到耦合长度和耦合系数之间的关系．设定波导的宽度为 1,μm，考虑到实际工艺的实现，设定耦合间距为0.5,μm．软件的设置如图5所示，图5(a)是器件的横截面，图 5(b)是器件的俯视图．设定光场从上面一根波导输入，随着光波的传输，光波会耦合到另一根波导中，仿真得到第一根波导的光场随着耦合长度的变化关系如图 6(a)所示，可以看到耦合系数和耦合长度呈现正弦振荡的形式，耦合周期大约为1,500,μm．图6(b)是波导耦合器中的光场分布．

改变两波导之间的距离可以得到耦合周期和耦合间距之间的关系，如图 7所示，从中可以看到耦合周期是随着耦合间距指数上升的关系，即

图4 耦合系数和Q值的关系(R=20.μm，λ=1.55.μm)Fig.4 Relationship between coupling parameter and Q(R=20.μm，λ=1.55.μm)

式中：Tc为耦合周期；拟合系数α= 1 .2647、β=0.797 0．耦合周期上升表示在固定的耦合长度下，耦合到另一根波导的光波减少．耦合到另一根波导的光场强度为

式中LΔ为耦合长度．式(21)定量地给出了耦合系数和波导器件的几何尺寸的关系．通常情形下，耦合长度远小于耦合周期，可以通过增加耦合长度和减少耦合间距的方法提高系统的Q值．

图5 软件设置Fig.5 Software configuration

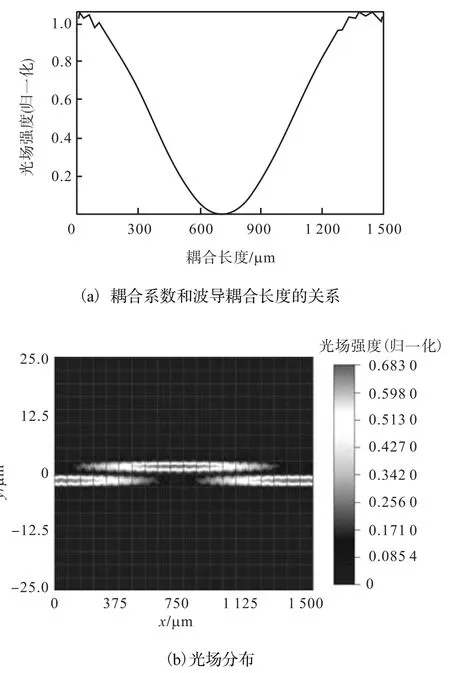
图6 数值分析仿真结果Fig.6 Numerical software simulation results

图7 耦合间距和耦合周期的关系Fig.7 Relationship between coupling space and coupling period

2.4 使用多环的结构

环形谐振器的Q值定义为[9]

以双环结构为例，与单环结构相比双环结构展宽了xFSR，同时减少了系统的谐振线宽[10]，即

对于多环结构可以反复使用式(22)～式(24)得到系统Q值．使用传递矩阵方法[10]对多环情形进行了计算，得出响应强度的曲线，如图8所示．可以看到环数提高有利于提高系统Q值．多环结构具有更高的Q值，因此系统延时减少，提高了电-光调制器的调制速度，也是一种提高微环电-光调制器调制速度的方法．

图8 多环串联谐振器的响应曲线Fig.8 Response curves of microring resonator

3 结 语

针对硅基调制器件提出了相应的光学和电学的理论模型，并在此基础上着重分析了影响硅基电-光调制器调制速度的因素，得出了比较简捷的光调制速度的数学表达式，该表达式可以方便地应用到实际的设计中．最后讨论了采用预增强脉冲、减小波导宽度、减小耦合系数和等效环形周长、采用多环结构等多种提高系统调制速度改善半导体环形电-光调制器的方法．本文的讨论对硅基光学调制器的设计和制作有一定的指导意义．

［1］Kobrinsky M J，Block B A，Zheng J，et al. On-chip optical interconnects[J].Intel Technology Journal，2004，8(2)：129-142.

［2］Reed G T. Device physics：The optical age of silicon[J]. Nature，2004，427(12)：595-596.

［3］Rong H，Jones R，Liu A，et al. An all-silicon Raman laser [J].Nature，2005，433(7023)：292-294.

［4］Xu Q，Schmidt B，Pradian S，et al. Micrometre-scale silicon electro-optic modulator[J].Nature，2005，435(19)：325-327.

［5］Gan F，Kartner F X. High-speed silicon electrooptic modulator design [J].IEEE Photonics Technol Lett，2005，17(5)：1007-1009.

［6］Soref R A，Bennett B R. Kramers-Kronig analysis of EO switching in silicon[C]//Proceedings of SPIE-The International Society for Optical Engineering.Atlanta，USA，1987：32-37.

［7］Xu Qianfan，Manipatruni S，Schmidt B，et al. 12.5 Gb/s carrier-injection-based silicon microring silicon modulators[J]. Opt Express，2007，15(2)：430-436.

［8］Soref R A，Schmidtchen J，Petermann K. Large single mode rib waveguides in GeSi-Si and Si-on-SiO2[J].IEEE Quantum Electron，1991，27(8)：1971-1974.

［9］Rabus D G.Integrated Ring Resonators[M]. New York：Spring，2007.

［10］Mandsen C K，Zhao J H.Optical Filter Design and Analysis：A Signal Processing Approach[M]. New York：Wiley，1999.