自升式钻井平台环境载荷及结构强度

吴小平，陆 晟

（上海船舶研究设计院，上海 200032）

0 引 言

自升式海洋钻井平台在海上油气开发中得到广泛应用。它由平台主体、升降装置以及若干（通常为3条到4条）桩腿组成。平台主体与桩腿之间可通过升降装置实现相对移动，桩腿底部设有沉垫或桩靴与海底相接触。作业时，桩腿降至海底，平台主体提升到海面以上一定高度，以避免波浪冲击。拖航时，平台主体降至水面，依靠浮力支承，类似于船体。此时，桩腿升至水面以上，通过拖航方式转移至新的作业地点。

自升式平台除了承受自身重量和可变载荷外，由于其工作环境的特殊性，还要时刻承受环境载荷的作用。还有由环境载荷引起平台结构的变形和振动，进而导致附加载荷的产生。例如：在环境载荷作用下，桩腿会发生变形，平台上部会发生很大的侧向位移，从而导致平台主体对桩腿底部产生附加弯矩。另外，当平台的自然周期与波浪周期接近时，平台会发生强烈振动，引起很大的动载荷。再者，由于环境载荷的持续作用，平台结构的内部将会发生疲劳损伤，久而久之，导致结构疲劳破坏。所以，在自升式平台结构设计过程中，要多方面、综合考虑环境载荷的影响。

1 环境载荷

海洋环境载荷主要来源于风、浪、流、冰、地震等方面。如果平台作业海域不是地震频发区或冰情严重区域，则地震载荷和冰载荷并非要考虑。相比之下，风、浪、流[1]等载荷对于任何一个自升式平台都必须考虑，对平台是否能正常工作起决定性作用。

1.1 风载荷

风载荷对平台的稳性和结构强度有很大影响，风载荷大小可由风压乘以投影面积得到。风压P可按下式计算：

式中：f——常数；

V——风速；

Ch——高度系数；

Cs——形状系数。

高度系数和形状系数的选取见参考文献[2]。由风压和投影面积，可算出风载荷 ：F

式中：A——平台在迎风面上的投影面积。

ABS（美国船级社）规定：正常钻井作业状态下设计风速不小于36m/s（70kn），风暴自存状态下设计风速不小于51.5m/s（100kn）。

1.2 波浪载荷

波浪载荷是环境载荷中的重要组成部分，对平台的极限强度、疲劳强度、振动等方面均有很大的影响。常见的波浪理论有：AIRY波、STOKES波、椭圆余弦波、孤立波、流函数等[3]。不同的波浪理论都有各自的适用范围，见图 1。在设计中应根据具体的波高、波浪周期、水深进行选取。一般来说，对于多数情况下的极限强度计算，STOKES 5阶波理论可以得到很高的精度；对于结构疲劳强度计算，由于波高较小，宜选用AIRY波理论。选定波浪理论后，可以得到波浪的速度势或流函数，于是水质点的运动速度和加速度也就随之确定。

图1 波浪理论适用范围

1.2.1 MORISON公式

由于自升式平台桩腿各组成构件的直径与波长相比非常小，可采用MORISON公式[3,4]进行波浪载荷计算。MORISON公式表达式如下：

式中：FW——作用在单位长度构件上的法向波浪力，由阻力 FD和惯性力 FI组成；

ρ——流体密度；

D和A——杆件直径和横截面积；

un和an——水质点的法向速度和法向加速度；

CD、CM——阻力系数和惯性力系数，统称为水动力系数。

应用MORISON公式的关键在于求取水动力系数。

1.2.2 水动力系数

对于桁架式桩腿，可以采用等效的方法来计算MORISON公式中的直径、截面积、阻力系数和惯性力系数。对于某一节距内的桩腿，具体做法如下[3]：

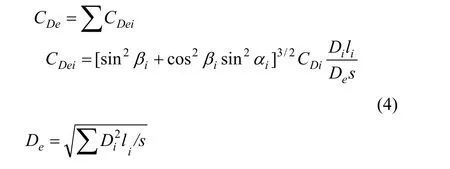
式中：CDe——等效阻力系数；

De——等效直径；

CDi——桩腿各组成构件（包括横撑、斜撑等）的阻力系数；

Di——构件直径；

li——构件长度；

s——桩腿节距；

αi——水流方向与构件在水平方向投影之间的夹角；

βi——构件相对于水平面的倾角。见图2。

图2 桁架式桩腿流向角

对于圆管构件，其阻力系数可查阅相关规范。根据管子外壁的粗糙程度，阻力系数的取值会有所不同。粗糙程度主要取决于海生物的影响，平台工作一段时间后，桩腿上会附有大量海生物，导致桩腿构件的尺寸和重量都有所增加，更重要的是，海生物的存在对水动力也有较大影响。通常认为位于平均水面 2m以上的构件不受海生物的影响，在计算水动力时，以光滑构件计算，而 2m以下则以粗糙构件计算。对于半圆型齿条型弦杆， CDi与来流入射角有关，可计算如下[3]：

式中：CD0——圆管的阻力系数；

θ——波浪相对于齿条弦杆的入射角。如图3所示。

图3 半圆型齿条弦杆阻力系数计算

同理，可以得到等效惯性力系数MeC[3]：式中：CMei——构件的惯性力系数，根据管子外壁的粗糙程度，可以在 1.8～2.0之间取值，光滑外壁取大值，粗糙外壁取小值。

1.3 流载荷

流速主要由潮汐、风暴涌、风所决定，ABS推荐如下的流速分布[2]，见图4：

式中：d——水深；

h——风对浪的作用深度；

z——参考深度；

Vc——总流速；

Vt、Vs、Vw——潮汐、风暴涌以及风所引起的流速。

根据作业地点的具体情况，也可以采用其它类型的流速分布，比如三角形分布、指数函数分布等。当波浪与海流同时作用时，应将流速和波浪所引起的水质点速度进行叠加，再进行波浪力计算。

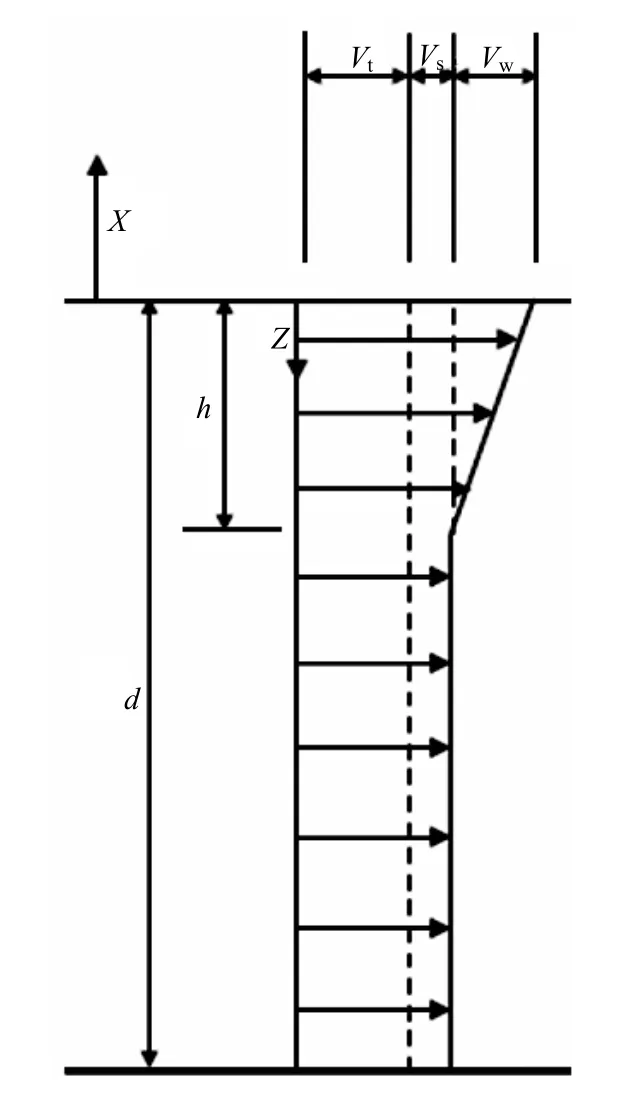
图4 流速分布形状

1.4 惯性载荷

大多数自升式平台的自然周期在 5s到 15s之间，这与海洋环境中常见的波浪周期很接近。在波浪和海流的周期性作用下，平台会随着波浪振动，特别是平台自然周期与波浪周期非常接近时，将会引起强烈共振，对平台造成很大破坏作用。平台设计中应考虑动态放大效应，目前有3种方法可以采用，分别为：单自由度方法、频域动态分析方法、时域动态分析方法。时域动态分析方法最为精确，推荐采用该方法，但是这种方法相对比较复杂，且计算量较大。所以，在初步计算时，通常都采用单自由度方法。该方法将平台模拟成一个有阻尼的弹簧振子系统，根据平台自然周期、波浪周期、阻尼系数，确定动态放大因子DAF，然后根据DAF和水动力来计算惯性力。DAF可通过下式计算[2]：

式中：Tn——平台的自然周期；

T——波浪周期；

ζ——阻尼系数。

根据ABS规范，若DAF＜1.05，表明动态放大效应并不明显，此时可以忽略动态放大效应对平台的影响。反之，应根据DAF进行惯性力计算。由动态放大效应引起的惯性力 Fin可由下式计算：

式中：B Smax、B Smin——最大波浪力和最小波浪力。

在计算波浪载荷时，通常选取若干个浪向角进行计算，以考虑不同方向的波浪对平台的作用。对于同一浪向，还要取多个不同的相位角进行计算，因为不同的相位角对应于不同的波峰位置，波峰位置不同，对平台的作用力大小也不同。所以，对于任一浪向，可以得到波峰位于不同位置时平台所遭遇的最大波浪力 BSmax和最小波浪力 BSmin。

1.5 P-DELTA效应

平台在环境载荷作用下会发生变形，导致平台产生横向位移，如图5所示。因此平台主体对桩腿将会产生附加弯矩作用。此时桩腿截面上将出现二次应力，即 P-DELTA效应。对于一般的结构，P-DELTA效应并不显著，但对于深水自升式平台来说，P-DELTA效应不可忽略。轴向载荷会改变构件的刚度，进而会影响侧向位移。可以通过有限元程序计算出平台的侧向位移，再根据抬升重量来求得P-DELTA效应所引起的附加弯矩。

图5 环境载荷作用下平台发生变形

2 拖航状态强度计算

自升式平台在完成作业后，需要从一处转移到另一处，这一过程称为拖航。按照气象条件，拖航可分为油田拖航和海洋拖航。拖航时，桩腿位于水面以上，重心升高，受风面积增大，平台在风浪中将会发生剧烈摇晃运动，对平台的稳性、强度（尤其是桩腿与主船体连接处）带来非常不利的影响。船级社规定，必须对拖航状态下桩腿的强度进行计算。计算时，摇晃运动所引起的动载荷可以由平台在某一周期下的摇晃幅度所引起的动载荷加上此时重力所引起的载荷相叠加而成。ABS规定，可采用如下方法进行计算[2]：

1)油田拖航：6o/+120%×M(6o)g

2)远洋拖航：15o/10s +120%×(15o)

式中：6o、15o——油田拖航和远洋拖航的摇荡幅值；

Tn——自然周期，可以通过经验公式或有限元软件计算得到。

Mg(φ)——平台倾斜角度φ时桩腿重力产生的弯矩。

以横摇为例，对于桩腿上任意一个微小质量mi，其运动加速度 ai计算如下：

式中：T——横摇周期；

r——横摇半径；

g——重力加速度；

φ——横摇幅值。

将计算出的动载荷与静载荷叠加后，即可进行强度校核。对于具有1前2后3条腿的自升式平台，横摇时，只需校核任意1条后腿的强度；纵摇时，如果纵摇中心偏后，则只需校核前腿强度。

3 疲劳强度计算

海洋平台的工作环境非常恶劣，在役期间要经历长期、连续和随机的环境载荷。环境载荷的持续作用将会使平台结构产生交变应力，长时间的交变应力会引起平台结构的疲劳损伤，当疲劳损伤累积到一定程度，将导致结构疲劳破坏[5]。如前所述，风、浪、流是作用于海洋平台的主要环境载荷，其中风和流对疲劳损伤的影响相对较小，而波浪则是导致疲劳破坏的主要载荷。疲劳分析方法可分为 2种：确定性分析方法和谱分析方法，两者最大的区别在于，确定性分析方法中采用的波浪为规则波，而谱分析方法则采用不规则波，不规则波由大量规则波线性叠加组成，更加接近实际海洋情况。现以谱分析方法为例加以说明。

3.1 传递函数

传递函数是描述循环应力幅值与波高比值随波浪频率变化的一种函数，是谱分析方法中计算应力响应的一个重要组成部分。在计算载荷响应的传递函数时，所考虑的浪向角应不少于7个，规则波的波浪频率应不少于30个。

3.2 波浪谱

海面上的波浪具有随机性，随机波浪可以由波浪谱来描述，波浪谱表明了波浪能量随频率的分布情况，最常用的波浪谱有PM谱和JONSWAP谱，后者在前者基础上乘以1个提升系数，通常用于未充分发展的海浪。

3.3 响应谱

在船舶与海洋结构物设计中，通常都假定由波浪与结构物所组成的系统为线性系统。根据这一假定，由服从高斯分布的波浪作用所引起的平台应力也应服从高斯分布，其幅值服从瑞利分布。由传递函数和波浪谱，可以得到应力响应谱，对响应谱进行统计分析，得到应力响应的方差、平均过零周期等统计信息，由于应力幅值符合瑞利分布，还可以得到任意应力水平的超越概率以及这一应力水平在整个应力范围内所出现的概率。

3.4 应力循环次数

疲劳分析中，关键之一在于计算应力循环次数。对于某一应力水平，根据其出现的概率，结合应力响应的平均过零周期以及某一海况发生的概率即可计算1年时间内结构在该海况下承受该应力水平作用的次数：

式中：nji——第j个海况下应力σi的作用次数；

pj——第j个海况发生的概率，可以由波浪散布图得到；

P(σi)——应力σi出现的概率；

Tz——应力响应的平均过零周期。

P(σi)和 Tz可以由响应谱求出。

3.5 疲劳损伤和疲劳寿命

选取合适的 S- N曲线，由 S-N曲线可以得出结构在某一应力水平作用下发生疲劳损坏的次数 N ，例如：DNV S-N曲线由如下方程所描述[6]：

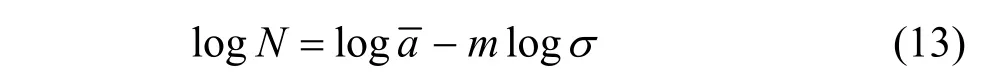
m—— S- N曲线斜率的负倒数；

σ——应力值；

N——循环次数。

由应力循环次数和 S-N曲线计算得到的循环次数，可以计算疲劳损伤。根据Miner线性累积损伤理论，结构总的疲劳损伤为各个海况下结构的疲劳损伤之和，由累积疲劳损伤即可得到疲劳寿命。

4 结 语

确定环境载荷以及由环境载荷引起的其它一些不利影响是自升式海洋钻井平台结构分析中的重点之一。本文总结了环境载荷中风、浪、流的计算方法，对波浪载荷，并对动态放大效应、P-DELTA效应进行了论述。并对设计中需要重点关注的拖航状态结构强度和结构疲劳强度等方面进行了分析研究。

[1] DNV Recommended Practice DNV-RP-C205.Environmental Conditions and Environmental Loads[S].2007.

[2] ABS.Rules for Building and Classing Mobile Offshore Drilling Units[S].2008.

[3] SNAME Technical and Research Bulletin 5-5A.Site Specific Assessment of Jack-Up Units[S].2002.

[4] DNV Classification Notes DNV-CN31.5.Strength Analysis of Main Structures of Self-elevating Units[S].1992.

[5] SACS FATIGUE USER’S MANUAL[S].EDI, 2005.

[6] DNV Recommended Practice DNV-RP-C203.Fatigue Design of Offshore Steel Structures[S].2008.