船体结构屈曲强度评估方法的规范研究及应用

洪 英，初艳玲

（中国船级社上海规范研究所，上海 200135）

0 引 言

1990年代后期，随着船舶结构的大型化和高强度钢的普遍应用，船舶结构的屈曲稳定性问题逐渐成为结构的主要失效模式之一。近年来，由于结构有限元直接计算技术的较快发展和趋于成熟，在直接计算中已开始引入屈曲强度校核要求。同时，随着结构屈曲稳定理论和计算预报准确性的进一步发展，人们逐渐突破了线弹性范围内保守的结论，开始引进了板格“后屈曲特性”，以期充分挖掘材料潜力、发挥结构的极限承载能力，也由此应运而生各种各样的屈曲强度设计衡准。

1 目前船舶结构屈曲强度评估方法

目前船舶结构屈曲强度评估方法由3大部分组成，第 1部分为类似最小尺度要求的细长比要求（slenderness requirements），第2部份为规范指定性屈曲要求（prescriptive buckling requirements，PR），主要为基于应力的基本板格与筋条/梁柱的抗屈曲要求、各种工况下船体梁构件、槽形舱壁总体屈曲、作为永久检验通道（PMA）的大腹板加强构件和舱口盖等构件的抗屈曲要求等，第3部分为利用直接计算进行强度验证的有限元分析中的屈曲评估方法（buckling requirements for FEA，以下称“有限元屈曲要求”）。

在求解方法上，又可分为解析法或闭合公式法（closed cell formulae，以下称“公式法”）、半数值法和（全）数值方法三大类。如细长比要求和规范指定性要求一般以公式法表征，在有限元屈曲要求中，既有公式法，如散货船共同结构规范，又有半数值法，如油船共同结构规范，以及数值方法，如中国船级社（CCS）的《油船船体结构强度直接计算指南》[1]和油船共同结构规范[2]中的非线性有限元方法。但对于非线性的数值求解方法，一般仅用于规范标准制定的相关研究工作，而不作为设计和审图项目中常用的工程应用方法。图 1为CCS的《油船船体结构强度直接计算指南》中用有限元数值方法求解板格弹性屈曲的模型边界规定和计算结果。

从屈曲要求的异同性上看，由于对细长比要求，大多基于欧拉弹性屈曲公式和经验，故各个规范标准对此方面的要求基本一致；在基于应力的规范指定性要求方面，对于承受单一应力组份的构件屈曲校核计算，公式的本构为构件的计算应力与其屈曲应力之比，对于纵或横向压缩应力与剪应力共同作用的应力状态，以板格为例，两个应力组份与其屈曲应力之比项的之间呈一种相互关系，又称“相关方程”。

图1 板格弹性屈曲模型边界规定和计算结果

值得一提的是，对于规范指定性要求的船体梁屈曲校核，存在着不同形式的规范应用，一种是按照船体梁屈曲校核采用国际船级社协会（IACS）UR S11统一要求中的模式，如油船共同结构规范第8节第1.4.2中的有关公式，另一种是采用纵、横两轴向压应力分别与切应力共同作用的屈曲相关形式，如散货船共同结构规范[3]中的第6章第3节3.1.2中的有关公式。此外，后者还要求对承受侧向载荷的曲板和加强筋作屈曲强度校核。

在有限元屈曲要求方面，由于可以通过有限元方法对板格平面内的复杂应力状态和材料及几何非线性力学行为进行相当准确的描述，因此除了继续保持线弹性范围内的屈曲要求，又引入了板格的“后屈曲特性”，以期充分发挥材料和加筋板格的极限承载能力。由此产生了如下节所述的各种方法论。此外，对于板格的定义（板格件不同板厚、不规则多边形）、应力的取法（是否采用Poisson effect（泊松效应）修正）等，也存在一定的差异。

2 有限元屈曲要求方法

在有限元屈曲要求中，可以基于“双向轴压＋边缘剪切”的复杂应力状态考查板格的屈曲响应，这是有限元屈曲方法的鲜明特点之一。

在有限元的屈曲校核中，公式法、半数值法和数值法均列入有关规范标准中。

1)公式法主流的技术背景是德国工业标准DIN 18800[4]，基于数百个模型试验，其他技术标准中的闭合公式一般均在该公式的本构关系上作进一步的修正和改进。如散货船共同结构规范中的有限元屈曲要求等。

2)半数值法的技术背景基于非线性大挠度薄板理论，且采用结合半解析方法编制软件进行求解，可以从理论上较为准确地预报加筋板格实际情况下的屈曲行为[2]，如油船共同结构规范中的有限元屈曲要求。

3)数值法则完全基于有限元力学模型的数值分析计算，其中，线性有限元分析即为有限元的线弹性屈曲模态计算，而非线性有限元分析是计入非线性因素，以及初始缺陷后的结构极限强度计算，即在计算历程上通过加载递增进行迭代试算，一直算到结构不能承受更大的载荷为止。

由于有限元的屈曲要求涉及到一些较为复杂的力学行为，如后屈曲和非线性以及极限强度等，故也有将应用在有限元中的屈曲方法称为高级屈曲方法（advanced buckling methods），并将闭合公式和软件分别称为高级屈曲公式和高级屈曲软件。

需要说明的是，DIN方法虽然基于大量的试验，且宣称考虑了极限强度，但却未直接考虑侧向载荷的作用，故在有些规范中的“加强筋屈曲”章节要求中列入了“侧向载荷的作用” 作为补充。半数值法的高级屈曲软件，虽然比全数值法的效率高，但对于有限元模型中成千上万的板格单元，仍需花费很多计算时间。

对于一些高级屈曲的规范，如油船共同结构规范，提出了方法一（M1）和方法二（M2）2种屈曲方法[3]，分别针对“允许局部板材屈曲及载荷重新分布下的屈曲能力”（见图 2）和“不允许载荷在构件之间的重新分布下的屈曲能力”（见图3）的两种屈曲失效行为的准则层次。换言之，M1对应于弹塑性阶段，采用极限状态（ULS）的失效准则，而M2则对应于线弹性阶段，采用正常服役状态（SLS）的失效准则。在规范的实施应用上面，对M1和M2的适用部位进行了明确的规定（如图4），从部位的重要性和受力特征上较为科学地划分了的屈曲判定准则。除M1和M2外，在规范“加强筋屈曲”章节中，同样有类似ULS的规定要求，如散货船共同结构规范。

图2 进入弹塑性的应力重新分布

图3 线弹性范围的应力分布

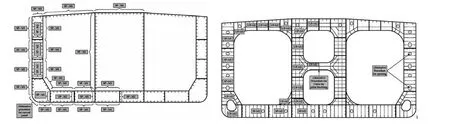
图4 针对不同部位使用不同屈曲校核方法的规定

3 非线性有限元加筋板格极限强度分析

非线性有限元方法属于数值分析法，可以模拟各种不同的结构布置形式，如非规则多边形、非平行筋条布置的加筋板格等，计算结果较为准确。但是，非线性有限元分析不同于常规的线性有限元分析，其方法较难掌握，且模型范围、单元尺度、边界条件、计及的初始缺陷等因素对计算过程和结果非常敏感，如处理不好，计算则不能收敛或得到似是而非的结果。此外，非线性有限元网格较密，计算规模较大，费时费力。因此，非线性有限元分析一般仅用于对其他非数值方法，如公式法和软件计算正确性的验证及校准，不适合正常设计和审图工作中的大规模屈曲校核工作。当然，对于个别复杂结构形式，如确需得到屈曲准确结果，也可以按个案处理进行专门的非线性有限元分析计算。

近年来，非线性有限元分析技术也得到较快发展，并引入到一些技术标准中，如在油船共同结构规范的附录D中，给出了非线性有限元分析的一些要求，如一些因素的考虑、非线性行为和材料特性的假定、初始缺陷和焊接残余应力，以及模型理想化（模型范围、单元尺度及边界条件）。CCS在这一方面也做了有益的探索和实践。非线性有限元分析的2个技术要点是：

1)边界条件的假定：对于“如果板格是大面积连续加筋板整体的一个部分，如底部或者舷侧板格，则其边缘可在面内自由移动，但应保持为直线。”[2,5]的规定，经过实践，可以采用类似“平行滑动（Slide）”边界运动形式（见图5）。在具体的计算实践中，采用MARC-mentat程序中的一些边界类型，起到了很好的模拟效果（见图 6）。

图5 平行滑动的边界移动形式

图6 平行滑动的边界移动形式在模型中的定义

2)初始缺陷的生成：初始缺陷对于非线性有限元屈曲分析而言，是一个重要的影响参数，包括制造的初始变形以及残余应力影响的因素。在初始缺陷的规定中，通常是采用“形状函数”模拟初始变形和焊接残余应力的影响，并用整体缺陷与局部缺陷合成为总体缺陷的方法生成计算的初始缺陷（见图7），其中整体缺陷表征加强筋偏离垂直板格平面的程度，局部缺陷表征板格板材的不平度，以及加强筋的侧向偏离程度（腹板、面板等）。根据能量原理，采用第一模态模拟局部缺陷，采用“形状函数”模拟整体缺陷，然后合成为总体缺陷。CCS的部分计算结果见图8～11[6]：

图7 初始缺陷的规定

图8 x、y轴向受压及边缘受剪模态

图9 单轴向工况下结构垮塌时的位移云图——非线性求解的结果（单轴向x）：

图10 单轴向工况下结构垮塌时的相当应力云图

图11 某一组合工况且加强筋一侧施加侧向载荷的位移

4 结构屈曲强度技术发展及展望

目前，包括CCS在内的各大船级社正在对船舶结构屈曲强度方面开展了更深领域和多方面的研究，并取得了一些成果，如计入侧向载荷作用的其他高级屈曲闭合公式的研究和推出，以及非线性有限元极限强度分析方法规则的制订等。这些成果，促进了计算过程的便捷、计算结果的准确，推动了高级屈曲理论的工程实用化和理性设计。

5 致 谢

美国MSC软件公司上海办事处和中国技术支持中心对本文相应工作给予了大力支持，在此深表谢意。

[1] CCS.油船船体结构强度直接计算指南[S].2003.

[2] 洪 英，等.IACS双壳油船共同结构规范高级屈曲评估方法及CCS新一代板格屈曲校核软件系统[J].上海造船，2008, (4): 32-38.

[3] IACS.CSR for Bulk Carriers and Background Documents[S].2008.

[4] DIN 18800, Part3, Nov.1990[S].

[5] IACS.CSR for Double Hull Oil Tankers and Background Documents[S].2008.

[6] 初艳玲.初始缺陷结构非线性屈曲分析方法中主要因素影响的敏感性研究[A].上海市造船工程学会论文集[C].2009.