基于ANSYS有限元简化模型的斜拉桥地震响应分析
辛亚军,陈 普,程树良
(1.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004;2.锦西化工机械集团有限责任公司,辽宁 葫芦岛 125001)
斜拉桥因其结构合理、外形美观、造价低、施工方便等突出的优点而成为世界上广泛采用的桥型[1],这种桥在地震作用下的响应特性越来越引起人们的关注[2]。以燕宏桥为例,进行ANSYS简化模型的地震反应有限元分析,分析结果为斜拉桥的抗震设计和加固提供参考。
1 工程概况
以横跨燕山大学东西校区的燕宏桥为例进行研究,该斜拉桥主桥为独塔双索面斜拉桥,跨度为(40+108+16+26)m,结构为墩、塔、梁固结体系。索塔横向造型为倒Y形,横向刚度大,有利于横向稳定。主跨拉索采用半扇形布置,横向采用A形双索面布置,有利于主梁抗扭。桥梁的立面图和俯视图如图1所示,桥梁共3组桥墩。
燕宏桥主体部分由主梁、斜拉索和索塔三大部分组成,部分材料参数如表1所示。

图1 燕宏桥结构示意
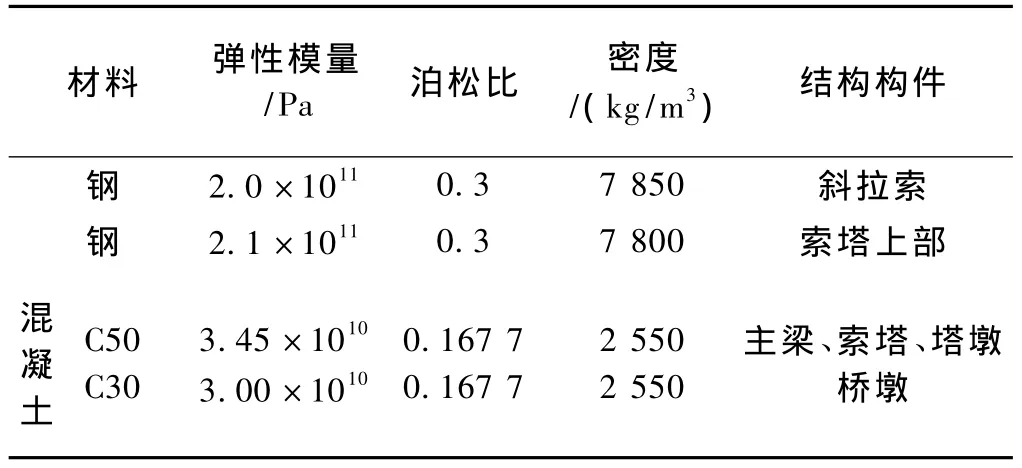
表1 材料参数
2 模型建立
首先建立燕宏桥的实体精细ANSYS模型,桥的模型根据桥梁的建筑施工图完成。主梁、塔墩、桥墩和索塔下部全部用SOLID65三维实体单元模拟,索塔上部用SHELL63壳单元模拟,拉索采用LINK10线单元[3],模型单元总数为41 171个。完成的有限元模型如图2所示。
桥墩及索塔下部桩嵌入地表,模拟为固接,索塔与主梁连接处为整体浇筑,使其黏合在一起。拉索锚固区结构形式十分复杂,无法按照真实情况建模,但其连接形式对整体模型影响不大,故采用塔及梁上自然节点建立拉索单元。
模态分析可以确定结构的动力特性,即桥梁的固有频率和振型。固有频率和振型是承受动态载荷结构设计的重要参数,是其他动力学分析的起点,例如谱分析、瞬态动力学分析(动力时程分析)。燕宏桥的前三阶振型和频率如图3所示。
如前所述的 ANSYS模型单元数量庞大,用 ANSYS进行地震反应分析比较困难,计算时间长,计算结果文件很大。因此,本文提出对有限元模型进行简化,总体原则是保持振动特性基本一致,方法是将箱型的主梁简化为混凝土实体梁,索塔简化为实体。简化模型如图4所示,简化模型与精细模型的前三阶频率对比如表2所示,可以看出误差不大,可以保证使用简化模型提供的计算结果与精细模型一致,用来作进一步分析。

图2 有限元精细模型

图3 斜拉桥模型振型和频率

图4 有限元简化模型

表2 精细模型和简化模型频率对比
3 燕宏桥地震反应分析
对燕宏桥进行地震作用下的反应分析,以Elcentro地震波为例,计算其纵向输入情况下燕宏桥的地震响应,加速度峰值调至4.0 m/s2(8级大震),如图5为Elcentro地震波的加速度时程曲线。

图5 Elcentro波加速度时程曲线
3.1 下部结构响应
高桥墩的破坏类型大多为弯曲型破坏,矮桥墩的破坏大多为剪切型破坏。燕宏桥的桥墩是实心桥墩,高度为8 m左右,不属于高桥墩,所以不容易发生弯曲型破坏。1#至3#桥墩底部剪切应力的时间历程曲线如图6所示。
由图6可以看出三组桥墩所受剪应力的情况非常近似,峰值也很接近,其中最大峰值出现在3#桥墩,绝对值为18.883 MPa。
3.2 上部结构响应
图7为桥面和索塔中部的加速度时程曲线,由图7可知,桥面中部加速度放大了3倍左右,索塔中部加速度放大了10倍左右,均在正常范围之内。

图6 3组桥墩剪应力时程曲线
图8为桥面结构和索塔中部位移时程曲线。通过对比可以看出,桥面最大位移出现在右侧4#桥墩处,其峰值为 -0.031 5 m,右侧边墩帽梁宽0.625 0m,在安全范围之内,不会发生落梁危险。
3.3 斜拉索响应
因为燕宏桥整体结构关于纵轴对称,而地震为纵向输入,所以对斜拉索的分析只需取一侧即可,图9为单侧14根拉索中正面和背面应力较大的两根索的应力时程图。
经过对索塔右侧A1-A11号索和背索B1-B3号索所受应力对比,可以看出背索变化速度较正面索变化速度快,是由于背索直接锚固于地表的缘故。全部14根拉索所受应力时程曲线基本保持一致,都在拉索初应力上下波动,峰值出现时刻大致相同,其中A7索峰值最大为 42.2 MPa,远远小于拉索的标准强度值1 670 MPa。
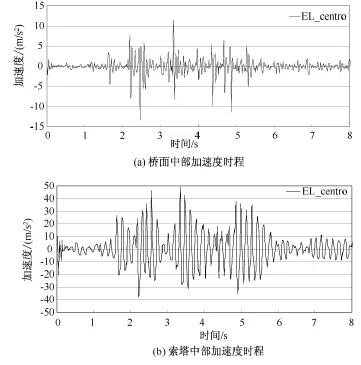
图7 上部结构加速度反应
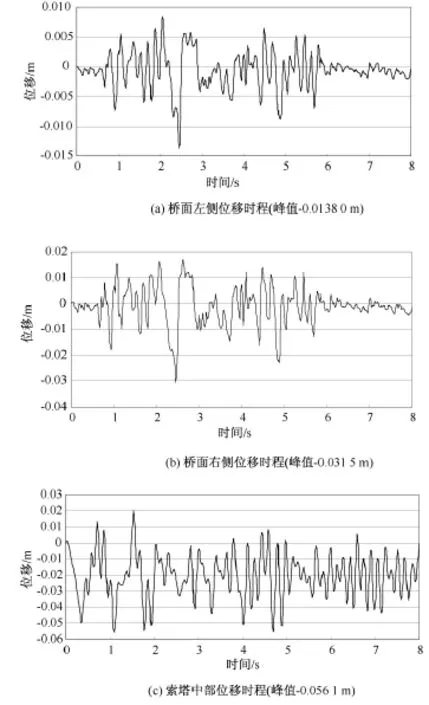
图8 上部结构位移反应

图9 索的应力时程曲线
4 结论
本文采用ANSYS针对一座斜拉桥分别建立了动力分析的精细模型和简化模型,在简化模型和精细模型动力特性一致的基础上,对简化模型进行了Elcentro地震波作用下的地震反应分析。分析结果显示桥梁的下部结构,包括塔墩和桥墩,在纵向地震作用下剪切应力曲线基本保持一致,数值相差不大;上部结构最容易发生的破坏是落梁,本例桥面最大位移在安全范围之内,加速度放大倍数正常;斜拉索最大应力值远小于极限值。本文采用的计算方法和分析结果可以为斜拉桥的设计和计算提供参考。
[1]林元培.斜拉桥[M].北京:人民交通出版社,2004.
[2]叶爱君,胡世德,范立础.斜拉桥抗震结构体系研究[J].桥梁建设,2002(4):1-4.
[3]张立明.Algor、Ansys在桥梁工程中的应用方法与实例[M].北京:人民交通出版社,2003.
[4]中华人民共和国建设部.GB 50011—2001 建筑抗震设计规范[S].北京:中国建筑工业出版社,2001.
[5]徐扬,王冲,周凌远.大跨高墩连续刚构桥地震响应分析[J].铁道建筑,2010(2):14-17.

