水电站水库优化调度的改进混沌遗传算法
吴学文,索丽生,王志坚
(1.河海大学计算机与信息学院,江苏 南京 210098;2.河海大学水利水电学院,江苏 南京 210098)
水电站水库优化调度是一个具有复杂约束条件的非线性优化问题,国内外不同的学者采用了不同的方法进行研究,取得了较多成果[1-2]。其中较常用的方法有动态规划方法(DP)[3-5]、逐次优化法(POA)[6]、大系统递阶法[7]、粒子群算法(PSO)[8]、遗传算法(GA)[9-11]等。但这些方法也存在明显缺陷:DP法占用计算机内存多,计算速度慢,存在维数灾问题;POA法易陷入局部的最优,使计算速度大幅度降低;大系统递阶法需增加协调因子,计算比较复杂,收敛速度慢;PSO算法存在精度不高和易陷入局部最优点的不足;GA算法存在接近全局最优时不易收敛、不容易处理复杂约束条件、搜索效率低等不足。近年来有学者研究了混沌优化算法在水电站水库调度中的应用问题[12-14],该算法具有参数简单、稳定性好、全局优化等优点,但存在以初值作为初始最优解、迭代效率有待提高、优化过程需要较大的混沌序列长度、程序运行时间长等局限性。因此,有必要研究应用更加有效的全局优化算法。唐巍等[15]将混沌融入遗传算法,提出了混沌遗传算法,对复杂函数优化进行了仿真研究,验证了其有效性。王文川等[16]研究了混沌与遗传算法的结合,结果表明其算法比传统遗传算法具有更好的性能,但其采用的是基本遗传算法。笔者将改进的遗传算法和混沌优化相耦合,增加混沌扰动算子,将2种算法优势互补,开发了改进的混沌遗传算法(ICGA),并探讨其在水电站水库中长期优化调度中的应用。
1 改进混沌遗传算法的基本思想
1.1 混沌优化算法
混沌优化算法(COA)是近年来随着混沌学科的发展而提出的一种新的优化算法。其基本思想是把混沌变量映射到优化变量的取值空间,构造混沌变量序列,充分利用混沌变量在混沌运动中所具有的遍历性、随机性、规律性来寻找全局最优解。李兵等[17]、骆晨钟等[8]提出了一类类似于载波的方法,将混沌映射产生的混沌变量引入到优化变量中,将混沌运动的遍历范围转换到优化变量的定义域,利用混沌变量进行优化搜索。由于混沌运动具有遍历性、随机性、规律性等特点,使得搜索更有效。水电站水库优化调度的混沌优化算法求解过程为:以水库水位作为决策变量,由Logistic方程生成n个混沌序列,并将其放大到各阶段水库水位的取值范围,然后利用混沌优化的机制进行迭代搜索,直到满足最大迭代次数或者误差精度要求,输出最优解。
1.2 改进遗传算法
GA起源于对生物系统所进行的计算机模拟研究,它通过模拟自然进化过程来搜索最优解,利用某种编码技术,作用于称为染色体的数字串,模拟由这些数字串组成的群体的进化过程。目前GA的编码主要有二进制码、格雷码和浮点码。基本遗传算法采用二进制编码,选择算子主要是采用轮盘赌选择,容易出现过早收敛,算法精度、可信度等方面也需要提高。

1.3 改进混沌遗传算法
混沌遗传算法(CGA)充分利用了混沌优化的遍历性和遗传算法的反演性,主要是将混沌优化算法与遗传算法集成,利用混沌优化的遍历性特点,弥补遗传算法容易陷入局部最优、收敛速度慢的缺陷,从而得到一种新型高效的优化算法[19]。
笔者开发的ICGA在将混沌优化算法与改进的遗传算法耦合时考虑了2种集成方式:第1种方式是一方作为附加成分被加入到另一方的搜索中。例如,在遗传算法中引入混沌优化算法,该算法通过混沌映射产生遗传算法的初始种群,然后在遗传算法的搜索迭代机制基础上通过搜索产生更优的最优个体,引导种群的新一轮进化。第2种方式是2种算法独立求解,其中一方利用对方的计算结果,但并不直接进入对方的搜索过程中。最常见的做法是,一旦遗传算法搜索到优异的可行解后,马上换用混沌优化算法求解。例如在遗传算法搜索过程中,增加混沌扰动后再进行迭代寻优,在最终得到最优结果时又根据混沌扰动机制,通过若干次混沌扰动进行细搜索,得到更好的搜索结果。
ICGA的基本思想是:首先采用第1集成方式,利用混沌映射得到混沌序列,将其通过载波方式放大到决策变量的取值范围,然后利用实数编码对决策变量进行编码,表示为染色体,并根据改进的遗传算法搜索机制对种群进行选择、交叉、变异操作,得到1组满足寻优终止条件的初始最优解;然后利用第2集成方式,将此组初始最优解对应的初始最优决策向量增加一个混沌扰动,利用混沌搜索机制进行若干次细搜索,得到问题的最优解。混沌扰动算子可以通过下述方法进行:
将满足寻优终止条件后的初始最优解(x1*,x2*,…,xn*)映射到(0,1)区间,得到初始最优决策向量,记为δ′,将混沌映射函数迭代K次后得到的1组混沌序列(K为该混沌序列的长度),设εk为该混沌序列中的第k个数值(k=1,2,…,K),记 δk为由n个εk组成的向量,称为混沌向量,则可通过式(1)求解混沌扰动后混沌决策向量δk′:
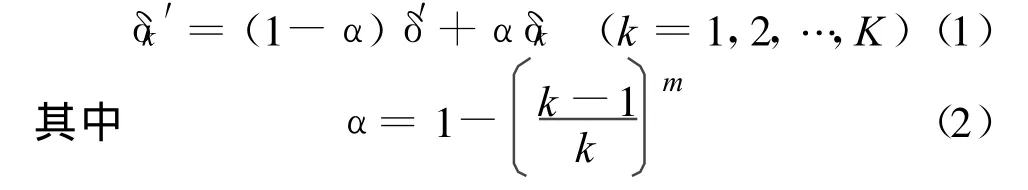
式中:α为(0,1)区间的某个数值,可通过采用自适应选取,在搜索初期α较大,随着搜索进行,逐渐接近最优,选用较小的 α,以便在(x*1,x*2,…,x*n)所在小范围内搜索;m为正整数,根据目标函数的个数确定,一般大于或等于2;k为混沌映射迭代次数。
2 ICGA计算步骤
ICGA求解水电站水库优化调度步骤如下:
步骤1 划分水电站水库调度期时段,确定优化变量及其范围。将调度期划分为T个时段,选择各时段的水库水位值作为优化变量,确定各时段水库水位值的取值范围[ai,bi]。
步骤2 参数设定。确定变量的个数,确定遗传算法的群体规模M、遗传算法的终止迭代次数N、最大交叉概率 pc-max、最小交叉概率pc-min、最大变异概率pm-max和最小变异概率pm-min。
步骤3 目标函数处理。当某个染色体对应的决策变量不满足约束条件时,将其适应度值取为接近于零的某个较小数值。直至概率搜索出来的染色体均能满足约束条件。
步骤4 初始化种群。Logistic映射如式(3):
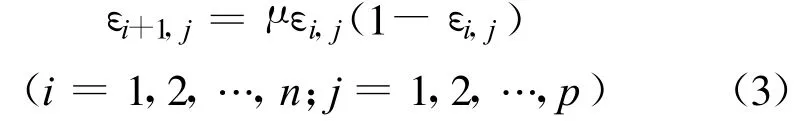
式中:μ为控制参量。设 0<ε1,j<1,μ=4时,系统完全处于混沌状态,具有混沌运动的所有特征,因此可作为优化算法中的混沌变量迭代方程。
选取n个不同初值,利用式(3)进行迭代,得到n个轨迹不同的混沌变量序列,将此混沌序列按式(4)放大到优化变量取值范围,作为初始种群。

式中:ai和bi分别为混沌变量xi,j的下限和上限。
步骤5 编码。选择浮点码对变量进行编码。
步骤6 选择、交叉和变异运算。采用随机联赛选择算子,交叉算子采用算术交叉,变异算子采用均匀变异,同时在交叉和变异运算中根据适应度值和进化代数来调节个体的交叉概率和变异概率。
步骤7 适应度值计算。选择适当的适应度函数计算适应度值。
步骤8 最优保留策略。将适应度值从大到小进行排序,选择种群中适应度最优的10%的染色体直接带入下一代群体。再次对全部种群进行选择、交叉和变异运算,计算新的适应度值并按大小进行排序,用上一代保留的10%的染色体替换种群中适应度值最差的10%的染色体,得到新的种群。
步骤9 初始最优解。种群重新排序,求适应度值的最大值与平均值的差值。如果此差值在设定的允许误差内,或迭代次数达到设定最大值,则寻优结束,输出初始最优解;否则转入步骤8。
步骤10 混沌扰动。对初始最优解对应的初始最优决策向量增加混沌扰动,混沌映射函数仍然采用Logistic映射,混沌序列长度为K,得到K组混沌扰动后的混沌决策向量。
步骤11 细搜索优化。将混沌扰动后的K组混沌决策向量放大到优化变量的取值范围,计算比较其相应的适应度值,适应度值最大的即为最优解,其对应的决策变量为最优决策变量。输出最优解。
ICGA算法计算流程见图1。
3 水电站水库优化调度模型
3.1 目标函数
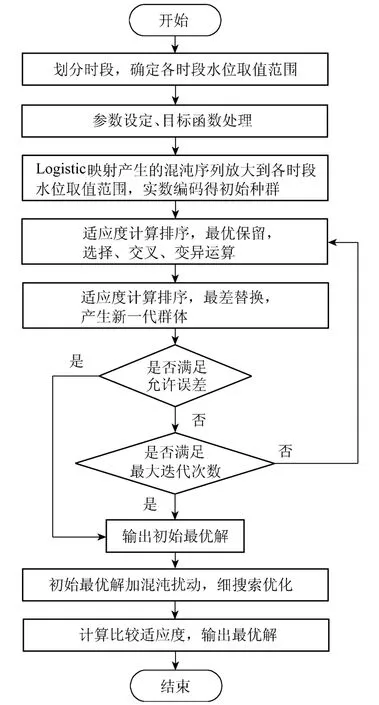
图1 ICGA算法计算流程
以发电量最大为寻优准则,在电力系统稳态运行的条件下用一个年周期内发电量最大作为水电站水库优化调度模型目标函数,即

式中:E为水电站的年发电量,kW◦h;A为水电站的综合出力系数;Qt为水电站在t时段的发电流量,m3/s;Ht为水电站在t时段的平均发电净水头,m;T为水电站调度年内计算总时段(本文计算时段为月,T=12月);Mt为第t时段的小时数。
3.2 约束条件

式中:Vt+1为水电站第 t时段末的水库蓄水量,m3;Vt为水电站第t时段初的水库蓄水量,m3;qt为水电站第t时段的平均入库流量,m3/s;Qt为水电站在t时段的发电流量,m3/s;St为水电站在t时段的弃水流量,m3/s;Kt为时段长度换算系数;Vt,min为水电站第t时段允许水库最小蓄水量,m3;Vt,max为水电站第t时段允许水库最大蓄水量,m3;Qt,min为水电站第t时段的最小下泄流量,m3/s;Qt,max为水电站第t时段的最大下泄流量,m3/s;Nt,min为水电站允许的最小出力限制,一般为保证出力,kW;Nt,min为水电站允许的最大出力限制,一般为装机容量,kW。
4 实例计算
选用某水电站资料进行实例计算。已知该水电站水库的水位~库容关系曲线和下游水位~流量关系曲线,水库总库容为 8.96亿m3,调节库容为4.45亿m3,正常蓄水位为 977.0m,死水位为948.0m,防洪限制水位为966.0m。电站综合出力系数取 8.3,保证出力为 185mW,装机容量为1080MW,最大过水能力为1000m3/s。采用多年平均入库径流资料,利用前述模型及算法进行优化调度计算,根据水库控制运用条件,7月份作为汛期,月初水位需降至死水位,其他月份的水位在死水位与正常蓄水位之间变动。模型中Logistic映射初值取值范围为[0.51,0.74],控制参量 μ=4,混沌序列的长度为1000,模型的初始种群取1000,交叉概率为0.9,变异概率为0.1,允许误差为 1.0×10-8,最大迭代次数为200,利用MATLAB软件编程计算,结果见表1。
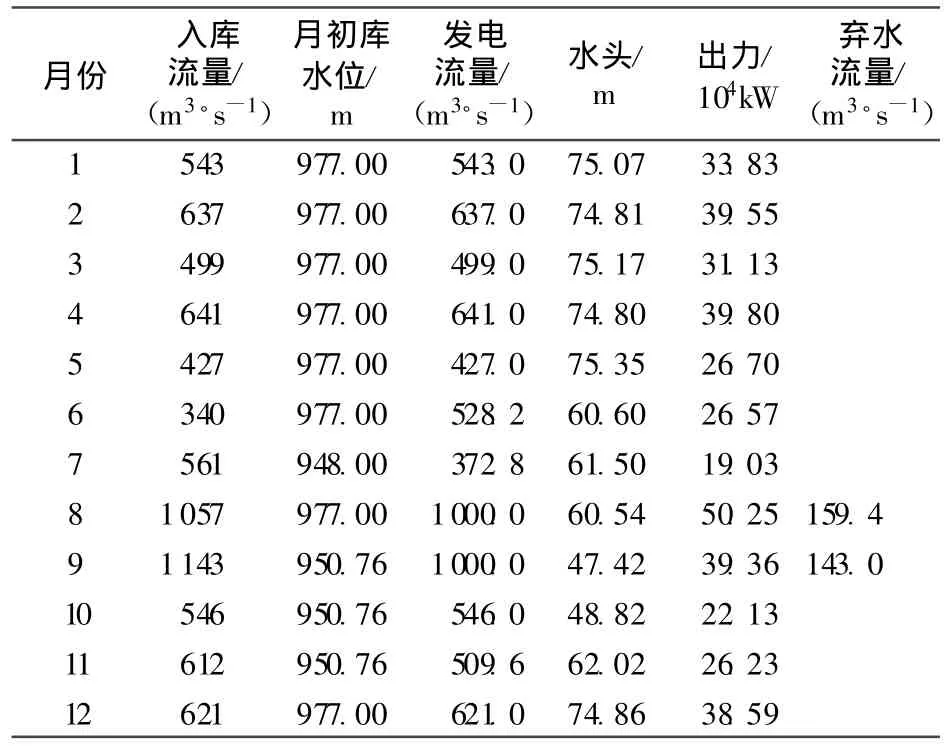
表1 ICGA算法求解水电站水库优化调度结果
为了进行比较,使用混沌优化算法和改进遗传算法进行求解,其目标函数和约束条件不变,混沌优化算法中Logistic映射初值、控制参量 μ、混沌序列的长度、混沌扰动算子等参数,以及改进遗传算法种群规模、选择算子、交叉算子、变异算子、允许误差、最大迭代次数等参数取值参考混沌遗传算法,取相同的数值,3种算法结果对比见表2。
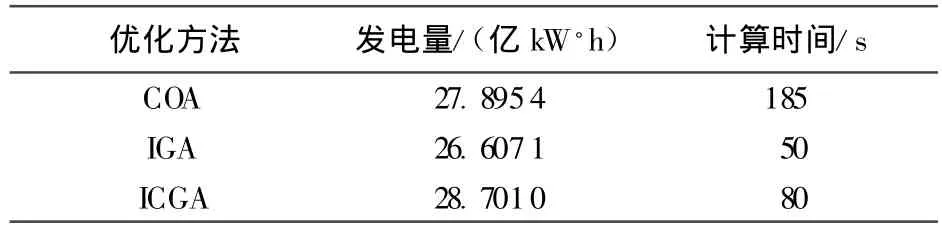
表2 3种算法计算结果对比
由表2可以看到,在相同的参数设定情况下,ICGA计算的年发电量最大,计算时间也较短,是最优方法。COA计算得到的年发电量大于IGA计算得到的年发电量,但需要较大的混沌序列长度,程序运行时间较长;IGA虽然是一种随机概率搜索优化方法,能以较短时间逼近全局最优,但求解结果不是最优;ICGA将混沌映射的遍历性特点和IGA的寻优机制相耦合,将具有遍历性的混沌序列放大到优化变量的取值范围,利用GA的搜索机制进行迭代搜索,能同时搜索解空间中的许多点,可以在占用少量内存的情况下更加逼近全局最优解。当然,ICGA由于需要较大的种群数来实现遍历性搜索,使得其计算时间比IGA略长,但比COA计算时间大幅度缩短。因此,ICGA因其自身特点,将给水电站水库中长期优化调度提供一种新的模型求解方法。
5 结 论
水电站水库优化调度是一个大系统复杂优化问题。笔者通过研究,提出了求解水电站水库优化调度问题的新方法——ICGA。该算法将水库水位作为优化变量,将调度期划分为若干时段,根据已知资料确定各时段水位的取值范围,利用混沌优化的遍历性特点,将Logistic映射产生的混沌序列放大到优化变量的取值范围,然后利用遗传算法的优化机制进行选择、交叉和变异运算,得到初始最优解。对初始最优解对应的优化变量加一混沌扰动,进行混沌细搜索优化,得到问题的最优解。ICGA具有搜索效率高、收敛性能好、能以较快速度收敛于全局最优解等优点,提高了水电站水库优化调度的效率和效益。当然,该算法还有需要改进的地方,即如果优化变量的取值范围太大,容易造成搜索时间长,结果偏差大。
[1]张勇传,李福生,熊斯毅,等.水电站水库群优化调度方法的研究[J].水力发电,1981,7(11):48-52.
[2]畅建霞,黄强,王义民.水电站水库优化调度几种方法的探讨[J].水电能源科学,2000,18(3):19-22.
[3]ROSSMAN L.Reliability-constrained dynamic programming and randomized release rules in reservoir management[J].Water Resources Research,1977,13(2):247-255.
[4]LITTLE J D C.The use of storage water in a hydroelectric system[J].Operational Research,1955(3):187-197.
[5]梅亚东.梯级水库优化调度的有后效性动态规划模型及应用[J].水科学进展,2000,11(2):195-198.
[6]张玉新,冯尚友.多目标动态规划逐次迭代算法[J].武汉水利电力学院学报,1988(6):72-82.
[7]黄强,颜竹丘.应用大系统递阶控制理论解梯级水电站水库群长期最优调度[J].水电能源科学,1993,11(2):80-87.
[8]王少波,解建仓,汪妮.基于改进粒子群算法的水电站水库优化调度研究[J].水力发电学报,2008,27(3):12-15.
[9]马光文,王黎.遗传算法在水电站优化调度中的应用[J].水科学进展,1997,8(3):275-280.
[10]钟登华,熊开智,成立芹,等.遗传算法的改进及其在水库优化调度中的应用研究[J].中国工程科学,2003,5(9):22-26.
[11]AHMED J A,SARMA A K.Genetic Algorithm for optimal operating policy of a multipurpose reservoir[J].Water ResourcesmAnagement,2005,19:145-161.
[12]梁伟,陈守伦,何春元,等.基于混沌优化算法的梯级水电站水库优化调度[J].水电能源科学,2008,26(1):63-66.
[13]邱林,田景环,段春青,等.混沌优化算法在水库优化调度中的应用[J].中国农村水利水电,2005(7):17-19.
[14]刘起方,马光文,刘群英,等.对分插值与混沌嵌套搜索算法在梯级水库联合优化调度中的应用[J].水利学报,2008,39(2):140-150.
[15]唐巍,郭镇明,唐嘉亨,等.复杂函数优化的混沌遗传算法[J].哈尔滨工程大学学报,2000,21(5):1-5.
[16]王文川,程春田,徐冬梅.基于混沌遗传算法的水电站优化调度模型及应用[J].水力发电学报,2007,26(6):7-11.
[17]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.
[18]骆晨钟,邵惠鹤.用混沌搜索求解非线性约束优化问题[J].系统工程理论与实践,2000,20(8):54-57.
[19]姚俊峰,梅炽,彭小奇,等.混沌遗传算法及其应用[J].系统工程,2001,19(1):70-74.

