若干农田降雨地表径流计算方法述评

孔莉莉,张展羽,孟佳佳

(1.河海大学水利水电学院,江苏 南京 200098;2.淮安市水利规划办公室,江苏 淮安 223005)

农田降雨地表径流预测是定量研究农田非点源污染物径流输出负荷的前提,对于防控因降雨冲刷作用引起的土壤侵蚀以及农田非点源污染问题有着重要意义。目前用于确定降雨径流量的方法多为直接求定法、水文学法、基于水量平衡与能量守恒的动力学法等。但由于农田降雨径流过程受降雨特征(降雨量、降雨强度、降雨历时等)、下垫面特性(土地利用方式、土壤质地等)以及农业管理措施等众多因素影响,农田降雨径流形成机理非常复杂,并且在以往针对自然区域的降雨径流模型中没有充分考虑作物水分管理措施对农田水文过程的影响。因此,针对国内外现有的各类降雨径流计算方法进行分析比较,讨论各自的优缺点,并在此基础上提出农田降雨径流预测研究中有待深入探讨的问题。

1 降雨地表径流总量直接求定法

1.1 基于统计理论的径流预测模型

应用统计分析法通常是根据降雨径流这个物理现象的实验观测资料,借助于影响径流过程众多因素中的某个因素或几个主要因素来建立与径流量之间的响应关系。常见的基于统计理论的降雨径流预测方法主要有单因子回归法、多因子线性回归法等。

1.1.1 单因子回归方程

张国华等[1]分析了南方红壤丘陵地区影响降雨地表径流量的降雨量、雨强、降雨历时、最大60min雨强、前期土壤含水量等主要因素,并分别拟合得出各因子与径流量的单因子回归方程,研究表明它们之间呈现出较好的相关性,其中降雨量、降雨历时与地表径流量之间多为二次、三次抛物线关系,而降雨强度与产流量则呈指数关系。而段亮[2]运用实测资料拟合得出太湖旱地降雨历时与累积径流量之间对数回归方程(模型):

式中:Rt为对应时间的累积径流量,m3;t为降雨累积径流时间,min;a和b为常数,与地表覆盖有关。

此类模型结构简洁,需用参数较少,但模型精度较差,在径流量预测应用中存在较大误差。

1.1.2 多因子回归方程

由于仅考虑降雨这一单因子不能全面反映降雨径流特征,众多学者开始考虑建立多个影响因子协同作用的降雨径流预测模型。其中,苏东彬[3]运用非线性回归方法拟合了地表径流量与降雨量、土壤前期含水量、地形条件和植被覆盖度等因子的多元非线性回归方程:

式中:R为地表径流量,mm;λ′为影响径流量产生的其他因子的综合系数;P为降雨量,mm;ω为土壤前期体积含水率;LS为无量纲地形因子;C为无量纲的地表植被覆盖度;a,b,c,d为常数。C取值按照各径流小区的实际地表植被覆盖率情况来确定;而对于LS的确定,通常采用Williams修正后的通用土壤流失方程MUSLE中给出的LS来表征,计算公式为

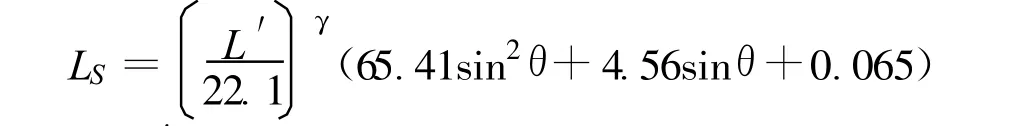
式中:L′为斜坡长度,m;θ为斜坡角度;γ为指数,γ=0.6[1-exp(-35.835tanθ)]。

多元统计模型虽然考虑了部分主要影响因子对降雨径流量的共同作用,在特定公式使用的资料范围内有足够的精度。然而在实际应用中并不方便,某些参数的确定必须要有完整的资料,难以应用于没有观测资料的区域,并且缺乏充分的物理基础,可移植性也较差。

1.2 基于人工神经网络的径流预测模型

截至目前,已有的基于统计理论的直接求定模型虽结构简单、便于计算,能够通过多次回归分析来描述径流量与几个影响因素之间的直接关系;但鉴于农田降雨径流与气候因子、下垫面条件以及人类活动等众多因素之间属于一种复杂的非线性关系,国内外学者开始尝试将人工神经网络中的BP网络模型引入农田降雨地表径流总量预测中来,这主要是由于人工神经网络是一种较好的模拟非线性输入输出关系的数学工具,而BP网络模型又具有较强的自学习能力和处理非线性问题的能力[4],且结构简单,性能稳定,善于从大量资料中分析提取宏观统计规律,同时也可用于降雨径流过程模拟。但是这类模型在建立过程中,输入输出因子的选取是关键,直接影响着模拟及预测的精度。刘阳等[5]在对输入因子选取问题处理上除将降雨强度、降雨历时、坡长、坡度与产流量有直接关系的因子作为输入因子外,提出将土壤、植被、水保措施和入渗等不易获得的因素综合起来用一个糙率因子替代后并同输入,结果表明该方法模拟精度较高,预测效果较为理想。此外,另有研究指出在主要影响因子选取上还可先用逐步线性回归、主成分分析、投影寻踪分类等方法将次要因子剔除后再结合人工神经网络BP模型使用,预测效果会更佳。

1.3 基于径流曲线法的径流预测模型

在众多的降雨径流总量计算模型中,美国农业部水土保持局20世纪50年代提出的SCS径流曲线法已得到公认和普遍推广。该方法计算过程简单,所需参数较少,资料易于获得,尤其适用于缺乏详细降雨过程资料的农业小流域,并且有效考虑了小流域的下垫面条件(土壤、坡度、植被、土地利用状况)以及前期土壤含水量等对降雨径流的影响,是一种行之有效的用来模拟小区域降雨产流总量的预测方法[6]。同时,利用该方法也可对降雨径流过程进行简单模拟。模型以简单的水量平衡为前提,在集水区的实际入渗量与实际径流量之比等于集水区该场降雨前的最大可能入渗量(或潜在入渗量)与最大可能径流量(或潜在径流量)之比的假定基础上建立[6],即

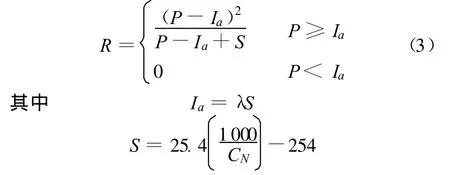
式中:Ia为雨量初损值(植物截留、初渗,填洼),mm;λ为初损率;S为潜在入渗量,mm;CN为径流曲线数。

SCS径流曲线公式最初开发应用于美国一些地区,其自然地理状况和水文气象条件与中国的研究区域存在较大差异。因此,在应用过程中有必要对模型的适应性和参数的合理性进行分析,以适应不同研究区域应用SCS法模拟和预测降雨径流总量的要求。

1.3.1 对Ia的修正

Ia受土地利用、耕作方式、灌溉条件、植物截留、下渗、填洼等因素的影响,它通常与该场降雨前潜在的入渗量呈正比关系,美国农业部水土保持局在分析了大量长期实验结果的基础上提出较为合适的比例系数为0.2,即Ia=0.2S。然而,Ponce等[7]研究发现,由于地区间自然地理情况和水文条件的较大变异性,λ不是一个恒定值,其值在0～0.3之间变化。随后王白陆[8]就此问题结合实例进行了深入研究,指出λ的变化范围不宜过大,同时给出了λ的适宜范围(0.15＜λ＜0.25)以及确定方法。

1.3.2 对CN的修正

径流曲线数CN是为估算小流域土壤的潜在入渗量S而给出的一个综合反映雨前小流域特征的无量纲参数,其主要取决于土壤类型、植被覆盖以及土壤雨前湿度等因素。因此,不同下垫面条件的 CN取值大不相同,在应用SCS法时同样要对其取值进行修正。贺宝根等[9]结合上海郊区水旱轮作农田的径流观测数据,经多次调试分别给出了水田和旱田的CN修正值,即旱作农田CN取值78、稻田CN取值93时模拟结果较为满意。

另一方面,在径流曲线公式中仅涉及由降雨量资料推算径流总量,没有考虑降雨历时和雨强对初损及CN值的影响,并且在应用时对前期土壤水分等级划分及土地利用管理方式分类过于笼统,主观因素较强,这些都会不可避免地影响模型的模拟精度及使用效果[6]。因此,王英等[10]结合黄土高原地表径流多以超渗产流形式存在的特点,将降雨强度因子引入了径流曲线公式,通过不断尝试,给出了比较适合黄土高原地区的降雨修正经验函数式(式(4))。经实际应用发现引入降雨强度修正函数显著提高了径流曲线模型的径流预测精度,具有一定的应用价值。

式中:Pa为对地表径流有直接贡献的降雨量(用其代替径流曲线公式中的总降雨量,所对应的雨强大于土壤入渗速率),mm;I30为最大30min降雨强度;¯I为每场降雨的平均雨强,mm/h;β为降雨强度修正系数。

2 降雨地表径流机理过程定量描述

2.1 基于水文学方法的产流过程预测模型

一次降雨产生的地表径流通常是指地表供水与下渗、蒸发、植物截留及填洼等综合作用后的地面积水。整个农田水体循环过程满足质量守恒定律。在早期研究中,白清俊[11]基于这一定律,通过分析农田水分各种消耗途径给出水量平衡表达式:

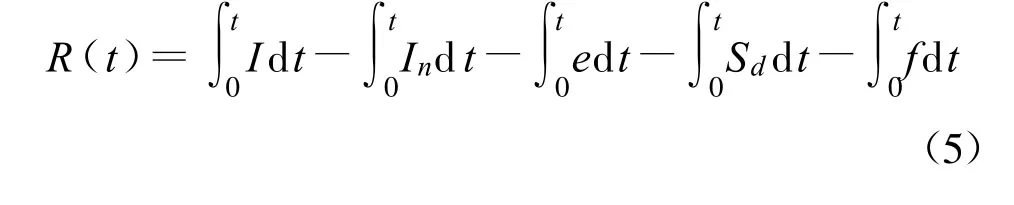
式中:R(t)为地表径流深,mm;I为降雨强度,mm/min;f为入渗强度,mm/min;e为蒸散发率,mm/min;In为植物截留率,mm/min;Sd为填洼率,mm/min。

若已知各变量与时间关系函数,可计算一次降雨的地表径流总量,同时可以获得降雨过程中各时刻的径流量。但在实际应用中取得各变量与时间函数的关系式较为困难,并且该方程(式(5))也未考虑到农田中作物生长过程的需水要求。另一方面,许多研究者为满足农业生产的实际需要,从水田和旱田的不同作物生长需水要求着手,结合较简单的降雨产流机制,推导出适用于水田与旱田作物生长的不同降雨产流模型[12]——水田产流模型及旱田产流模型。

2.1.1 水田产流模型

水田产流计算主要考虑的因素有水田的适宜水深上限H1与下限H2、耐淹水深H3、水田的下渗及灌排方式。因此,水稻生育期中任一时段的农田水分变化可采用水量平衡方程递推得[13]

式中:Ht+Δt为Δt时段末计算所得的田间水层深度,mm;Ht为 Δt时段初计算所得的田间水层深度,mm;PΔt为 Δt时段内的降雨量,mm;WCΔt为 Δt时段内的田间耗水量(包括稻田腾发量和下渗量),mm;mΔt为 Δt时段内的灌溉水量,mm;dΔt为 Δt时段内的排水量,mm。

若已知时段内的降雨量、田间耗水量以及时段初的田间水层深等,可递推时段末的田间水层深度,再与水稻的适宜水深和耐淹水深进行比对分析,确定是否进行排水,即可获得时段出流量,而累积排水出流总量则为此次降雨的径流累积总量。

2.1.2 旱田产流模型

旱作物生长要求在耕作层(土壤计划湿润层)土壤内保持适宜的含水量,通常以田间持水量为上限,凋萎系数为下限。对于旱作,在整个生育期内降雨过程中的任何一个时段,土壤计划湿润层内的水量平衡方程[13]为

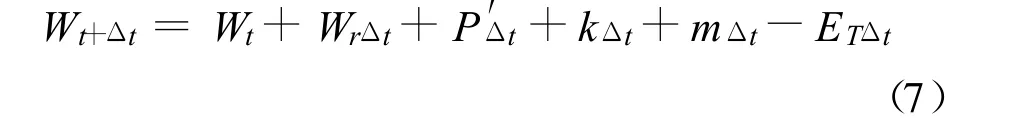
式中:Wt和Wt+Δt分别为时段初和时段末土壤计划湿润层内的储水量;WrΔt为Δt时段内随计划湿润层增加而增加的水量,若在该时段内无湿润层增加则无此项;P′Δt为Δt时段内保存在土壤计划湿润层中的有效雨量;kΔt和ETΔt分别为 Δt时段内地下水补给量及作物田间需水量。

旱田的整个计算过程及产流机制描述类同于水田。修正后的水量平衡方程式(式(7))虽能较全面地描述水田和旱田中不同作物生长条件下降雨径流总量及过程量与各变量之间的函数关系,但该方程中降雨强度、入渗强度、植物截留率、蒸散发率以及填洼率等关键要素仅是时间的函数。然而事实上这些变量不仅受制于时间因素,而且是多个因素共同作用的结果。例如入渗强度除与时间有一定关系以外,还取决于下垫面条件(土壤质地、前期土壤含水量等)。因此,徐志红[14]针对这一问题,指出对于某一时刻的田块来说,降水量、渗漏量、蒸散量、排水量、灌水量、作物吸收量、土壤蓄积量之间存在着复杂的非线性关系:

式中:F为土壤入渗量,mm;E为田间蒸发量,mm;D为排水量,mm;I′为灌水量,mm;W为土壤含水量,mm;C为作物吸收量,mm。

方程(8)虽然物理意义明确,涵盖较为全面,但由于方程式中各变量与相应影响因子间的函数难以确定,导致模型求解困难。因此在实际应用时多把方程中难以获取的参数项在满足假定条件的前提下进行简化处理,这样势必会影响到模拟精度。

2.2 基于水动力学方法的产流过程预测模型

随着对降雨径流机理过程研究的深入,各国学者开始着手将水动力学知识应用到降雨径流这一复杂过程的模拟中来。一般地,在不考虑根系吸水与田面蒸发等机制的前提下,农田降雨径流过程主要用入渗过程和坡面漫流过程两部分来描述。早期的研究中,入渗过程通常可用土壤水分运动基本方程表示[15];而坡面漫流过程则多用圣维南方程为基础建立的不同非线性运动波方程来描述,主要包括水流连续方程和动量方程[16]。但因影响降雨径流的因素众多以及大量参数的难确定性,再加上模型求解困难,机理性模型发展较为缓慢,直到现阶段计算机技术的高速推进,农田降雨径流机理性预测模型才得到较好的开发应用。其中,张书涵等[17]通过天然降雨条件下坡地水量转化机理的分析,提出了描述降雨入渗、坡面径流和土壤水分运动的坡地水量转化动力学模式。模型中采用了坡面承雨强度、饱和含水率结皮修正系数等概念,并考虑了坡度、坡向和雨滴倾斜对坡面接受降雨的影响及结皮对入渗量的影响,经野外试验数据检验,模型精度较高。之后,张国华等[1]又对其进行修正,除考虑植物截留、下渗等因素对产流过程的影响以外,还着重分析了降雨初始动量、风向、雨强变化以及表面张力等各种因素对坡面薄层水流的影响,实现了对农田降雨入渗产流过程的实时模拟,模拟结果更加符合实际;但是仅对水流运动沿坡面纵向进行了一维模拟,同时忽略了坡面横向上降雨和入渗的空间变异性以及降雨过程中的风向变化,因此,在今后的研究中还需要进一步改进。

3 结 语

目前,虽然国内外许多学者对自然降雨条件下农田地表径流流失机理及其影响因素都做了大量研究,并在此基础上提出了众多计算方法,但这些方法多是针对自然区域开发的以植物截留、下渗、填洼、蒸散发等作用要素为主来建立降雨径流模型,而将作物水分管理因素纳入其中进行综合考虑的农田降雨地表径流模型研究较少[18];另一方面,从现有模型的应用方面来看,还多是借用相对简单的经验模型,而对能够描述农田降雨入渗产流这一复杂机理的模型,因其参数众多,率定困难等因素,应用较少。因此,针对这一系列问题,在继续深入探讨农田降雨入渗产流机理过程的基础上,开发一套集土壤入渗、蒸散发、作物截留及水分管理等多模块于一体的,能充分反映农田产汇流机理过程的农田降雨径流机理性模型,对进一步防控因降雨冲刷作用引起的土壤侵蚀以及农业非点源污染问题有着重要作用。

[1]张国华,张展羽,左长清,等.坡地自然降雨入渗产流的数值模拟[J].水利学报,2007,38(6):668-673.

[2]段亮.太湖流域典型旱地氮磷向水体迁移特征研究[D].合肥:安徽农业大学,2006.

[3]苏东彬.太湖地区典型农业小流域非点源污染研究[D].南京:河海大学,2007.

[4]赵鹏宇,徐学选,王玉,等.黄土区不同土地利用方式下径流量的神经网络模拟[J].水土保持通报,2008,28(5):144-147.

[5]刘阳,李海英,王连元,等.基于BP神经网络的坡面降雨产流预测[J].吉林大学学报:信息科学版,2007,25(2):188-191.

[6]房孝铎,王晓燕,欧洋.径流曲线数法(SCS法)在降雨径流量计算中的应用——以密云石匣径流试验小区为例[J].首都师范大学学报:自然科学版,2007,28(1):89-92.

[7]PONCE V M,HAWKINS R H.Runoff curve number:has it reachedmAturity[J].Hydrologic Engineering,1996,1(1):11-19.

[8]王白陆.SCS产流模型的改进[J].人民黄河,2005,27(5):24-26.

[9]贺宝根,周乃晟,高效江,等.农田非点源污染研究中的降雨径流关系——SCS法的修正[J].环境科学研究,2001,14(3):49-51.

[10]王英,黄明斌.径流曲线法在黄土区小流域地表径流预测中的初步应用[J].中国水土保持科学,2008,6(6):87-91.

[11]白清俊.黄土坡面细沟侵蚀带产流产沙模型研究[D].杨凌:西北农林科技大学,1999.

[12]朱映新.苏州市降雨径流关系及下垫面变化对径流量影响研究[D].南京:河海大学,2007.

[13]郭元裕.农田水利学[M].北京:中国水利水电出版社,2002:34-39.

[14]徐志红.靖江市水稻大田种植期非点源氮污染负荷计算及控制对策[D].南京:南京理工大学,2002.

[15]宋孝玉,康绍忠,沈冰,等.黄土区不同下垫面农田降雨入渗及产流关系的数值模拟[J].农业工程学报,2005,21(1):1-5.

[16]黄新会,王占礼,牛振华,等.水文过程及模型研究主要进展[J].水土保持研究,2004,11(4):105-108.

[17]张书函,康绍忠,蔡焕杰,等.天然降雨条件下坡地水量转化的动力学模式及其应用[J].水利学报,2009,40(4):55-62.

[18]代俊峰,崔远来.基于SWAT的灌区分布式水文模型:Ⅰ模型构建的原理与方法[J].水利学报,2009,40(2):145-152.

[19]王船海,王娟,程文辉,等.平原区产汇流模拟[J].河海大学学报:自然科学版,2007,35(6):627-632.

[20]吴伟,王雄宾,武会,等.坡面产流机制研究刍议[J].水土保持研究,2006,13(4):84-86.