浅析“折线式底板”地基反力分布规律
郭树华 陈 崑
(上海勘测设计研究院 上海 200434)
目前,对于地基反力分布规律的研究主要侧重于不同基础形式下地基反力的分布规律,如独立基础、条形基础、箱型基础、片筏基础等,而对于折线式底板下地基反力的分布规律研究分析则很少。本文应用Plaxis有限元计算软件对“折线式底板”地基反力分布规律进行数值模拟,并就影响地基反力的诸多因素,如底板厚度、上部荷载、地质情况、底板两端倾斜角度等进行了系统的分析。
1 PLAXIS程序简介
PLAXIS程序是荷兰开发的岩土工程有限元软件。该程序能够计算平面应变问题和轴对称问题,能够模拟包括土体、墙、板、梁结构,各种元素和土体的接触面,锚杆,土工织物,隧道以及桩基础等。
2 计算模型和参数确定
为了考虑各因素对地基反力分布规律的影响,需要建立具有一定代表性的模型。因此本次数值模拟取底板混凝土强度等级C25,E=28GPa,厚度取 1.0m,底板水平段长5m,出水流道∶底板水平段∶进水流道=1∶1∶1,底板进水流道端高出0.5m,底板出水流道端高出1.5m;模型中底板下土体采用Mohr-Coulomb模型,土体参数∶γunsat=19.0kN/m,γsat=20.1kN/m,弹性模量为 E=1.15×104kPa;泊松比 γ=0.30;地基土的凝聚力C=63kPa;地基土的内摩擦角φ=17°。模型尺寸如图1。
3 计算方案设计
影响底板地基反力分布规律的因素很多,针对各种因素单独计算工作量很大,因此对计算方案有必要进行合理的设计。本文针对其主要的影响因素,确定计算方案如下:
(1)底板刚度的影响:通过调整底板的厚度来调整底板刚度的大小,分别取底板厚度为0.5m,1.0m,1.5m,2.0m;
(2)上部荷载的影响:分别取100kN/m,200kN/m,250kN/m,300kN/m;
(3)地质情况的影响:通过改变Mohr-Coulomb模型中土的弹性模量来模拟不同土质的影响,分别取E=1×104kN/m2,E=4 ×104kN/m2, E=7 ×104kN/m2,E=10 ×104kN/m2,E=20×104kN/m2;
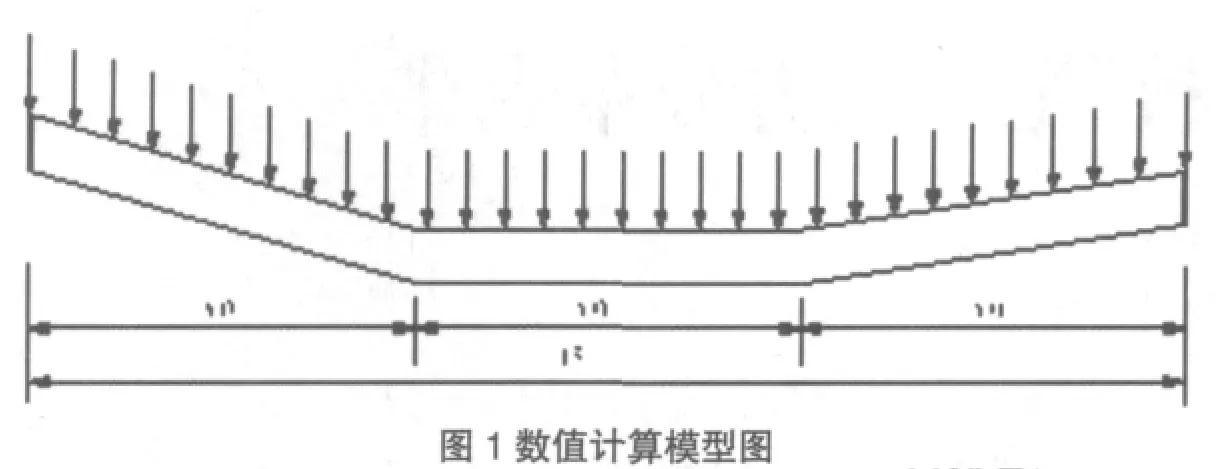

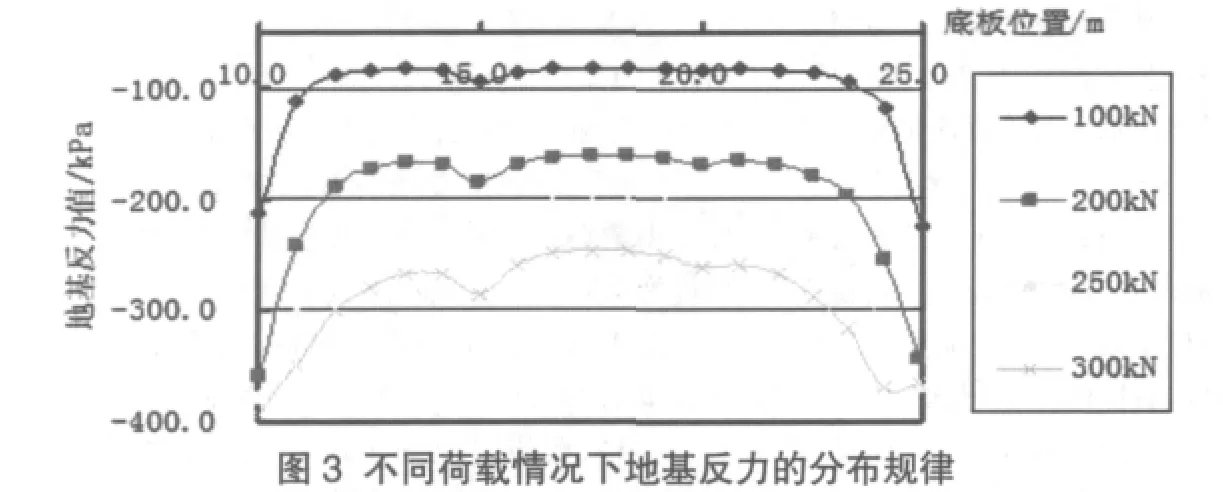
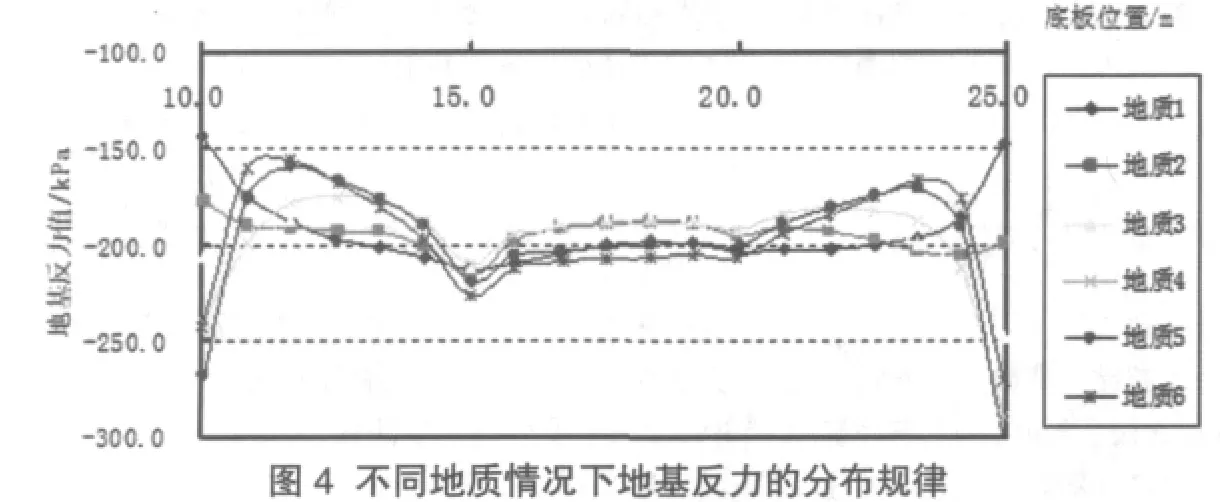
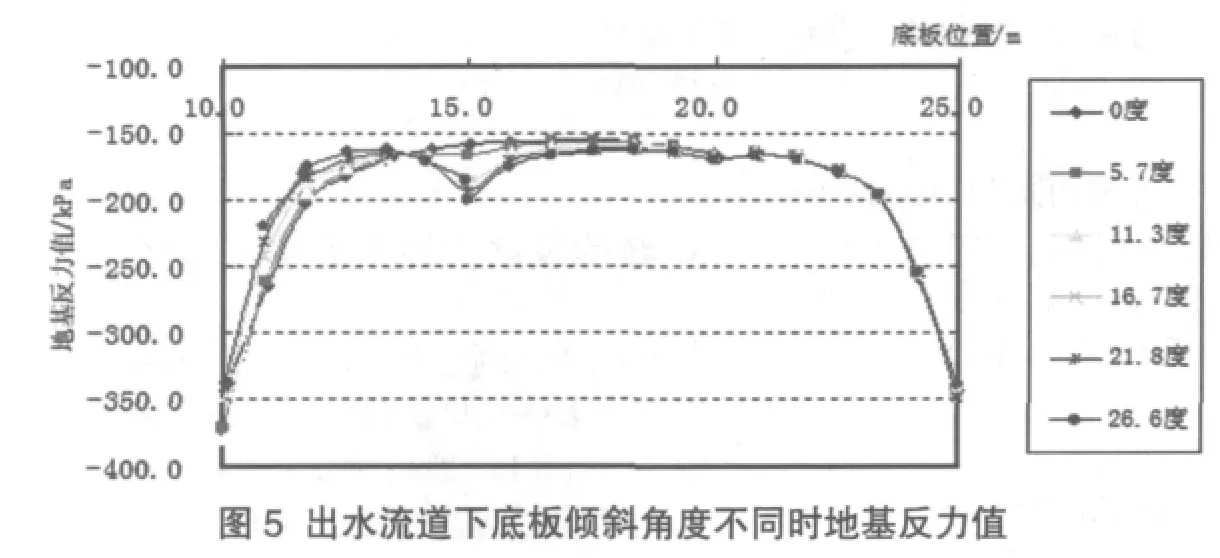

表1 地质材料参数表
(4)底板两端倾斜角度的影响:进水流道端底板角度固定为8°,出水流道端底板角度通过改变出水流道端点处高程来调节,分别抬高取 0m(0°),0.5m(5.7°),1.0m(11.3°),1.5m(16.7°),2.0m(21.8°),2.5m(26.6°)。
4 Plaxis有限元计算成果分析
(1)底板刚度的影响
底板的刚度一般与底板的厚度相关,不同厚度的底板其刚度不一样,对底板厚度分别取0.5m,1.0m,1.5m,2.0m来计算相应情况下地基反力的分布情况。
计算成果分析与讨论:从图2中可以看出,在荷载和地基土质相同的情况下,地基反力总是呈“M型”。
①进水流道下底板地基反力值比出水流道地基反力值要小,也就是倾斜角度小的底板地基反力值要大。②随着底板厚度的不同,底板出水流道段与底板进水流道段地基反力值都是在逐渐的增加。而底板水平段的地基反力值却在相应的减小。③底板出水流道与底板水平段交点处、底板进水流道与底板水平段交点处地基反力随底板厚度增大均减小。
(2)上部荷载的影响
底板地基反力分布情况与建筑物的上部荷载大小相关,分别取 100kN/m,200kN/m,250kN/m,300kN/m 计算相应情况下地基反力的分布情况(如图3)。
计算成果分析与讨论:①随着上部荷载的变化,地基反力与上部荷载也在同倍增长。②上部荷载越大,底板出水流道与底板水平段的交点处应力越大,且上部荷载越大时,底板出水流道与底板水平段的交点处应力集中越明显。
(3)地质情况的影响
数值模型计算中土体为Mohr-Coulomb模型,因此涉及到的材料物理力学参数主要有:变形模量E、泊松比γ、土体的内凝聚力C和内摩擦角φ。数值模型中混凝土按C25强度选取,E=28GPa。分别取土的弹性模量见表1。
计算成果分析与讨论:从图4中可以看出,在荷载相同和底板出水流道倾斜角度相同情况下,(1)地基反力随着土质的由弱到强,地基反力的分布规律也由开口向上的抛物线向“马鞍型”转变。(2)底板出水流道与底板水平段交点处地基反力值,地质4<地质3<地质1<地质2<地质5。底板进水流道与底板水平段交点处地基反力值地质3<地质4<地质2<地质1<地质5。
(4)底板两端倾斜角度的影响
底板两端倾斜角度的影响:进水端底板角度固定为8°,出水端底板角度通过改变出水流道端点处高程来调节,分别取 0m(0°),0.5m(5.7°),1.0m(11.3°),1.5m(16.7°),2.0m(21.8°),2.5m(26.6°)。
计算成果分析与讨论:在荷载相同和地基相同情况下,(1)出水流道下地基反力随底板倾斜角度增大而变小,底板水平段地基反力随底板倾斜角度增大而增大,进水流道下地基反力随底板倾斜角度变化基本不变。(2)底板出水流道与底板水平段交点处地基反力随底板倾斜角度增大而明显增大,底板进水流道与底板水平段交点处地基反力随底板倾斜角度增大基本无变化。
5 结语
底板地基反力分布规律与土体的性质、底板的形式、底板的刚度、作用的荷载等诸多因素有关,是一个较为复杂的研究课题,对其结构的受力形态尚缺乏全面的认识。本文采用Plaxis有限元软件对影响底板地基反力分布规律的几个因素(上部荷载,地质情况以及底板两端倾斜角度)进行数值模拟,具体表现在以下几个方面。
(1)地基反力随底板厚度不同,地基反力总是呈“M型”,但倾斜角度小的部分底板地基反力大,并且底板出水流道段与底板进水流道段地基反力值都是在逐渐的增加,而底板水平段的地基反力值却在相应的减小。另外底板出水流道与底板水平段交点处、底板进水流道与底板水平段交点处地基反力随底板厚度增大均减小。
(2)通过改变Mohr-Coulomb模型中土的弹性模量来模拟不同土质的影响,随土体的压缩模量增大,地基反力的分布规律也由开口向上的抛物线向“马鞍型”转变。此外,随地基土承载力的提高,基底反力向边缘集中的趋势将会加大。
(3)随出水流道下底板倾斜角度增大,出水流道下地基反力而变小,底板水平段地基反力增大,进水流道下地基反力基本不变。此外,随出水流道下底板倾斜角度增大,底板出水流道与底板水平段交点处地基反力明显增大,底板进水流道与底板水平段交点处地基反力随底板倾斜角度增大基本无变化。陕西水利
[1]钱玉林,洪家宝,杨鼎久等《土力学与基础工程》,中国水利水电出版社,2002.169-175.
[2]《建筑地基基础设计规范》(GB50007-2002)
[3]孙文科.建筑物基底反力的实时检测与分析.地震学刊,21(6)
[4]凌道盛,陈云敏,丁皓江,任意基础板的有限元分析[J],岩土工程学报,2000年第4期
[5]袁勋.高层建筑大底盘框架厚筏变形特征及基底反力试验研究,建筑科学,1998年第1期

