甚低频大气噪声中的MSK通信系统仿真*

付 贞 温 东 姜 波

(海军潜艇学院 青岛 266071)

1 引言

甚低频电磁波具有传播距离远、隐蔽性好、信号稳定,能穿透海水等优点,是各国海军进行海上远距离通信和水下通信的重要手段。与其它频段的通信系统相比,目前国内外对甚低频通信系统的研究较少,且大部分为不公开的。为了进一步加强甚低频通信研究,探索提高甚低频通信系统性能的有效途径,有必要对甚低频通信系统进行建模仿真和性能分析[1]。

MSK是甚低频通信系统的主要信号调制方式,MSK信号波形包络恒定、相位连续、频谱滚降快、频带利用率高、产生带外干扰小,抗干扰性能好,广泛应用于世界主要发达国家的甚低频通信系统中。

本文对甚低频通信系统的主要干扰源—大气噪声的特性进行分析,建立大气噪声的仿真模型,进而建立甚低频MSK通信系统的计算机仿真模型,给出仿真结果,并进一步分析噪声中各成分对甚低频通信系统性能的影响。

2 大气噪声模型

讨论通信问题,必需对接收机的前端噪声进行建模。为此需要一个可合理描述大气噪声特性,并适合甚低频通信系统仿真计算的噪声模型。

甚低频频段的大气噪声主要是由雷电瞬时放电引起的,它是高斯白噪声背景下的脉冲噪声。高斯白噪声是由分布于世界范围内的大量雷暴形成的脉冲的叠加构成,脉冲噪声是由接收机附近的闪电电磁脉冲叠加形成,脉冲能量极强,持续时间短,噪声能量主要集中在脉冲成份中[2]。

噪声在到达接收机之后,首先通过的是接收机的前端滤波器,所以观察到的大气噪声实际上是某个接收机滤波器的通带上的窄带噪声。

如果滤波器的带宽足够窄,则可以合理地认为其输出端的噪声为一个近似的高斯过程。这是由于经过窄带滤波后的噪声是许多独立的雷电放电成分的总和,并且其中没有任何一种成分占主导地位,此时运用中心极限定理,可认为它具有高斯特性[3]。实验数据指出,在甚低频系统中要实现这种情况,所需的带宽应小于50Hz,所以在实际系统中,这种高斯假设并不总是物理可行的。

由于对甚低频通信运用,接收机带宽相对于频带中心频率来说充分地小,一般来说是中心频率的10-2左右,这使得接收到的大气噪声可被假设为一个窄带随机过程。在实际系统中,这个假设条件几乎总可以满足,并且远非高斯假设那么严格,因此噪声的建模问题可以被简化。

对大气噪声的测量数据指出,这种噪声在低振幅部分具有高斯特性,在高振幅部分具有近似于指数正态分布的包络。由于较高的振幅对任何通信系统的性能都具有较大的影响,因此模型侧重于大气噪声的指数正态特性[4]。用以下形式将大气噪声模拟为一个具有指数正态包络的窄带过程[5～6]:

a(t)=Aen(t)sin[ω0t+θ(t)] (1)其中n(t)是一个实平稳高斯过程,其均值为0,方差为σ2n。A是一个常量(由噪声功率估计确定),θ(t)是随机相位过程,它独立于高斯过程n(t)。对大气噪声瞬时频率分布的测量结果表明,θ(t)与窄带高斯噪声的频率分布相似,也就是说,即使大气噪声的包络分布与高斯噪声在大包络值时相当不同,但它们的相位和频率分布却十分类似。因此假定θ(t)具有类似于窄带高斯过程的相位的特性。这意味着在任何给定的时刻t0,相位θ(t0)为一个均匀分布于[0,2π]上的随机变量,并且它独立于包络。

大气噪声的指数正态窄带噪声模型由式(1)给出。噪声的包络为

考虑包络的平均电压和rms电压。平均电压为

3 仿真模型[7～8]

MSK信号的时域表示可用以下公式表示:

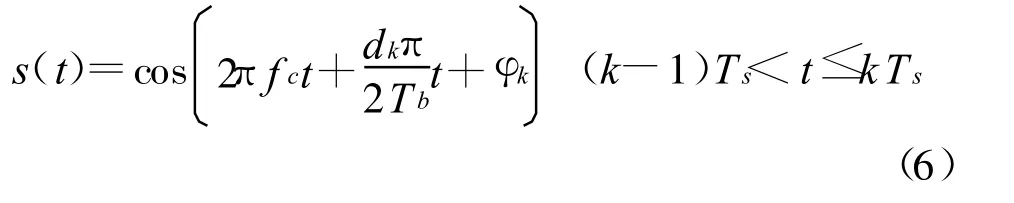
式中:fc为载波中心频率;其载频 f1、f2为 fc±1/4Tb;dk=±1;Tb为码元宽度;φk为第k个码元的初始相位。

对信号进行解调,采用相干解调法,其原理如图1所示。

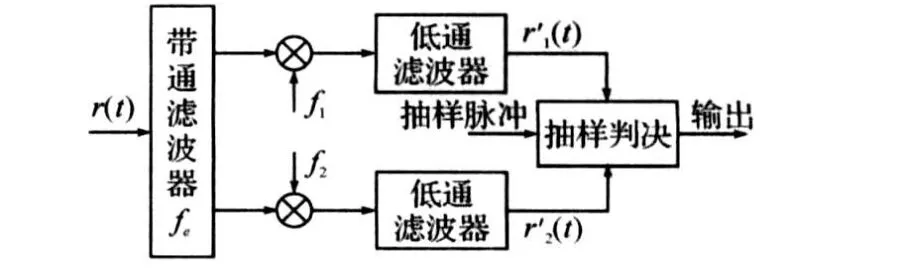
图1 MSK信号相干解调法

通信接收机接收到的信号为

抽样脉冲在t=(n-1)Tb+Tb/2时刻进行采样。采样单元后的抽样判决器比较两路输入波形,判断输入码元为“1”或为“0”。判决规则如下:

利用Matlab程序对系统进行了蒙特卡罗仿真,图2为原理图,共分为下列几个程序模块:

1)信源:产生均匀分布的“0”、“1”码元序列,并将其转换成适合MSK调制的双极性码。

2)调制、解调模块:按照MSK调制解调原理产生MSK信号,并从接收到的MSK信号中恢复出码元信息。

3)噪声源模块:产生指数正态分布的随机噪声包络,同时产生均匀分布的随机相位,通过输入的信噪比和电压偏差来控制噪声比例,最后合成大气噪声。

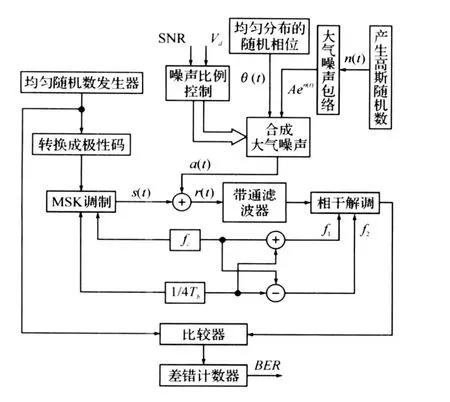
图2 系统仿真模型

4)误码计算主程序:进行误码率计算并产生Ber曲线。发送端的信息码元经过延迟后,与解调器输出的码元进行比较计算,两者不等时判为错码,同时记数器累计加1。

考虑到在仿真过程中,若按照实际系统的参数来进行仿真,则每个码元上的采样点数将非常高,可能达到103的数量级,而且在调制解调过程中的滤波处理所需的计算量十分大。另外,如果要得到接近真实的误码率结果,需要对大量的码元进行计算,一般来说,错误的码元数应在几十个左右才能保证结果与实际系统的性能相接近,这样的话,码元数目将达到106个以上。也就是说每次误码率的计算需要处理的信号样本点个数为109以上,普通的计算机很难完成这样的任务。

这里对程序进行了这样的处理:在误码计算时,采用先进先出处理,每发送一个码元,就立即对其进行调制、传输和解调,并判断是否为错码,然后再进行下一个码元的传送。设置一个误码最大个数B和码元最大个数N,当误码个数小于B时程序持续运行,当个数达到B时停止运算;同时为了防止程序进入死循环,如果码元数大于N时,也停止运算。这里B的值取50～100之间,N的值取106～ 108之间。

4 仿真结果

分别取Vd=2.5,Vd=4.5,Vd=7,按照式(1)所给的模型对大气噪声进行仿真,仿真结果如图3所示。可以看出,在较小的 Vd值(Vd=2.5)时,噪声的脉冲成分所占的比例出较小,此时噪声主要表现为高斯特性,而当Vd的值增大,噪声中的脉冲成分也会增加,瞬时脉冲的峰值也会随之变大。此时脉冲成分中集中了噪声的大部分能量,它将对系统的误率性能产生显著的影响。

图3 大气噪声仿真时域图

系统误码性能仿真结果如图4。由于对系统性能产生主要影响的脉冲噪声的随机性,使得误码率—信噪比曲线并非一条平滑的曲线,而是总体上有较规律的下降趋势但小范围内随机分布的点。

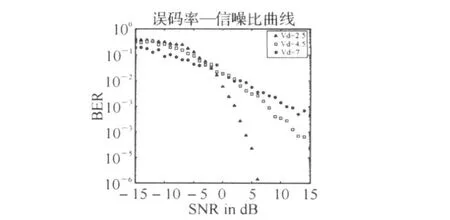
图4 甚低频大气噪声下MSK系统误码性能

在Vd=2.5时,由于脉冲特性表现的不明显,此时的误码率曲线较为平滑,在低信噪比时误码率为三种状态下最高,但随着SNR的升高,BER下降的速度最快,这与系统在高斯噪声下的性能十分类似。

然而实际的大气噪声中的Vd是不可能这么小的,随着Vd的增大,系统在低信噪比时误码率变得稍低,但BER随SNR升高而下降的速度明显变得缓慢了。其原因为:此时对系统产生主要影响的为大气噪声中的大幅度脉冲成分,由于脉冲时间短,幅度极大,仅靠增大信号发送功率无法削弱其对系统误码性能的影响。

5 结语

本文对大气噪声环境中的甚低频通信系统进行了建模、仿真,其中,通信信号采用的是MSK调制方式,对大气噪声的仿真使用了指数正态模型。在调整仿真中所用到的参数的同时,得到了不同情况下的大气噪声,它们中的脉冲成分所占的比例不同,从而它们的特性、对系统的影响也十分不同。仿真的结果得到了大气噪声下的误码率—信噪比曲线,通过对这此曲线的分析,可以看出,通信系统的接收性能会受到大气噪声的影响,其中脉冲成分比例增加的同时,系统的接收性能会随之变得衰弱。

文中的模型不仅可用于噪声性能分析,还可以用于对甚低频通信系统的进一步研究,例如接收性能的预测和评估。特别地,对于进一步探寻有效抑制大气噪声,从而提高系统性能的途径,具有一定的实际意义。

[1]张文娟,王永斌,付天晖.甚低频/低频通信中大气噪声仿真研究[J].舰船电子工程,2006

[2]Jim K.Omura,Paul D.Shaft.M odem Performance in VLF Atmospheric Noise[R].IEEE Trans.Commun,1971,com19(5)

[3]CCIR.World Distribution and Characteristics of Atmospheric Radio Noise[R].International Telecommunications Union,Geneva,Switzerland,Report 322-3,1986

[4]沃特.甚低频无线电工程[M].北京:国防工业出版社,1973

[5]W.H.Tranter,K.S.Shanmugan,T.S.Rappaport,et al.Principle of Communication Systems Simulation with Wireless Applications[M].New York:Pearson Education,2004

[6]Ranjan K.Mallkand.Anup K.Gogoi.An Optimum Detector for Coherent M-ary Signaling in the Presence of Impulsive Noise[J].IEEE T rans.Commun,2000

[7]梁高权.甚低频波和超低频波的辐射与传播[M].武汉:海军工程大学电子工程学院,2002:308～309

[8]韦岗,季飞,傅娟.通信系统建模与仿真[M].北京:电子工业出版社,2007