基于FPGA的高动态P码直捕算法设计与实现

吴华兵,胡永辉,何在民,王 康

(1.中国科学院国家授时中心,陕西 西安710600;2.中国科学院精密导航定位与定时技术重点实验室,陕西西安710600;3.中国科学院研究生院,北京100039)

0 引 言

在采用直接序列扩频体制的卫星导航系统中,P码序列周期长,码速率高,相对于民用的短周期测距码(民码),具有更高的保密性、抗干扰能力和测距精度,因此在军事领域获得了广泛的应用。

P码的直接捕获一直是国内外学者研究的重点和难点,早期的捕获方法是先捕获民码,再根据该码和P码的相位对应关系来实现P码的捕获,然而,这种方法用于军事领域的P码依赖于民码,大大削弱了系统的性能,当民码不可用时,就无法完成P码的捕获。因此,为了提高卫星导航系统的对抗能力,在民码受到攻击或关闭时的电子战和导航战环境中,军用导航接收机要能正常工作,实现P码的快速直接捕获就成为必然趋势。

Yang提出的XFAST方法,其思想是将本地伪码进行扩展和折叠来覆盖更大的时间不确定区间[1];Pang等人提出的重叠平均法,其思想是将本地伪码及其位移序列进行加权求和后,再对这一新序列进行大采样点数的平均来降低后续的计算量[2];近年来国内外很多学者采用基于FF T的伪码相位并行搜索来实现捕获[3-4]。以上的这些方法在码相位时间不确定度太大(如±1 s)或载波多普勒频率偏移过大时,都存在捕获时间长、消耗硬件资源庞大等问题。针对此问题,采用部分匹配滤波器组实现伪码时域并行搜索,将匹配滤波器组输出的部分相关值使用小点数的FFT进行功率谱分析,实现载波多普勒频率偏移的并行搜索。可以适当选择部分匹配滤波器的段数和FFT的点数,来实现所希望达到的多普勒频率搜索精度和搜索范围。

首先,介绍了基于匹配滤波器组与FF T伪码捕获的基本原理,推导了系统的数学模型,详细说明了硬件实现方案,给出了仿真及硬件测试的结果。

1 匹配滤波器组与FFT伪码捕获原理

1.1 系统的基本结构

匹配滤波器组与FFT伪码捕获的基本结构如图1所示,从ADC进来的数字中频数据同本地载波NCO混频,将数字中频数据下变频到基带,同本地复现码一起送入匹配滤波器组,然后将匹配滤波器组输出的部分相关值送入FFT模块进行功率谱分析,最后把FFT输出的结果送入检测判决模块进行信号检测。其中匹配滤波器是建立在序列相关的思想之上的,其捕获原理是以本地静止的伪码作为匹配滤波器的抽头系数,让ADC进来的采样数据顺序滑过本地序列,使每一个时钟周期产生一个相关值,当两序列零相移的时刻,就会产生一个相关峰值。FFT变换的意义是从频域上对信号进行分析,一个固定频率的正、余弦信号在频谱图上是一条单一的谱线,而高斯白噪声含有所有的频率,其FFT变换后是无限宽的频谱。当本地P码和接收序列P码相位对齐的时候。完成P码的剥离;短期内剥离P码之后的信号是基带数据符号调制的近似固定频率的正、余弦信号,此固定频率即为载波多普勒频率。此时信号经过解扩处理,其信噪比较高,则信号经过频谱变换后在频谱图上是一条单一的谱线;非理想情况下,是一束窄带谱线:由于信噪比较高,该谱线的幅度明显超过了其他噪声谱线。根据谱线的幅度明显超过了其他噪声谱线。根据谱线的幅度幅值就可以进行码相位和载波多普勒频率的估计,完成P的捕获。

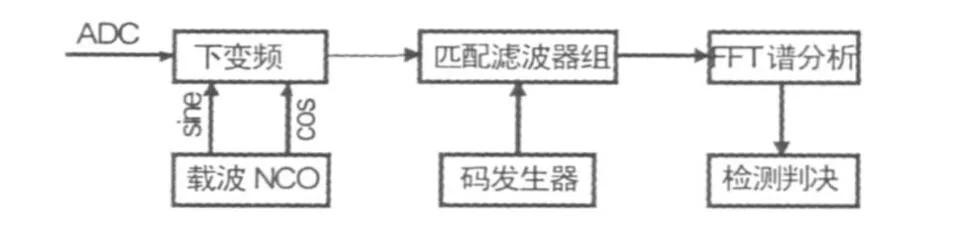
图1 匹配滤波器组与FFT伪码捕获的基本结构

1.2 系统的数学模型

卫星下行信号经过射频前端,由ADC转换成数字信号,在不考虑多普勒对码速率的影响和数据位影响的情况下,接收机端单颗星的P码信号模型为

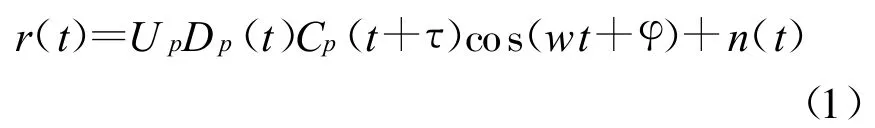
式中:Up为信号幅度;Dp为调制的数据;Cp(t+τ)为一定延时的P码;w=2π(fI+fd);fI为数字中频频率;fd为载波多普勒频移;n(t)是均值为0,方差为σ2的带限高斯白噪声。

同本地载波混频后,进入匹配滤波器组的信号模型为

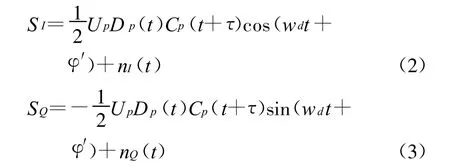
式中,nI(t)、nQ(t)为进入匹配滤波器组的噪声。

在接收机端,需要通过预检测积分时间(prediction integration time)提高信噪比,设整个系统的预检测积分时间为PIT,将它分为n段,每段的积分时间为T=PIT/n。令采样频率为 fs,则第m段的部分匹配滤波器的结果如下:

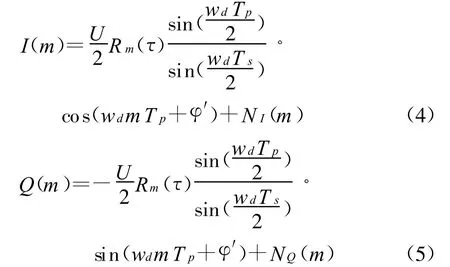
式中,Ts是采样间隔,Rm(τ)是部分积分时间 Tp内的码相关。令Z(m)=I(m)+jQ(m),进行N(N≥n)点的FFT

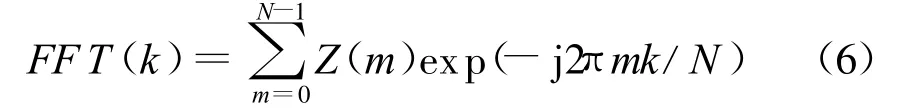
式中,k=0,…,N-1,则FFT的实部和虚部分别为

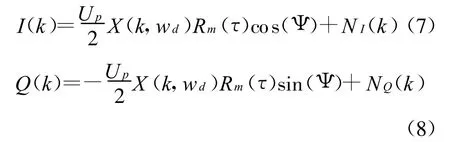
式中:

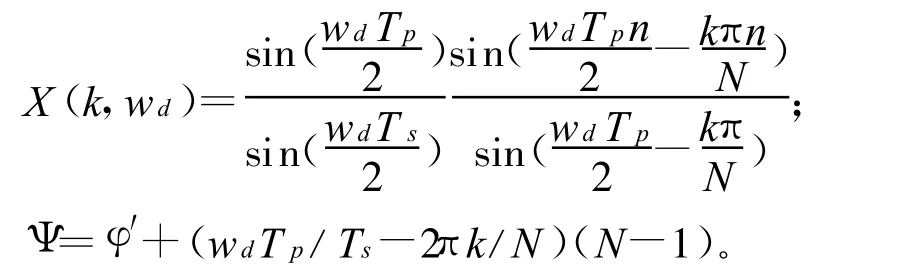
将I(k)2+Q(k)2送入检测判决模块,当接收的P码与本地P码对齐时,可得Rm(τ)=1,对应的即为捕获到的码相位和多普勒频率偏移。

2 P码直捕方案设计

系统的实现方案如图2所示,ADC进来的数据下变频到基带后,通过m点累加而取代一般的FIR滤波,大大减少了硬件的资源消耗和实现难度;将m点累加后的数据同本地P码一起送入匹配滤波器组进行码相位搜索,将匹配滤波器组输出的部分相关值送入N点FFT模块对多普勒频率偏移并行搜索,最后,把FFT输出的值送入信号检测判决模块。

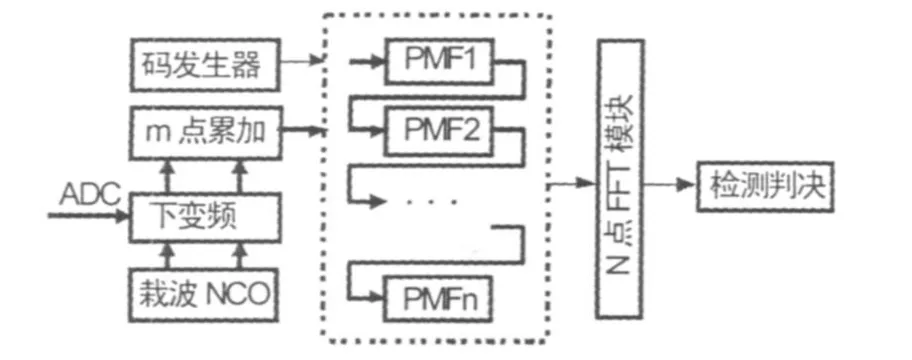
图2 匹配滤波器组与FFT捕获的实现方案

2.1 系统参数选择

由于P码的码速率较高,而且要满足一个码片最少有一个采样点,因此,采样频率也比较高,采样数据量大。对下变频到基带的信号进行m点累加,一是降低采样率减小整个系统的计算复杂度,二是对下变频后的信号做一次低通滤波,去除下变频过程产生的高频分量。m的选择要权衡到整个系统的运算量和m点累加后所带来的信噪比损失。

信号经过m点累加后进入匹配滤波器的量化位数近似正比于匹配滤波器消耗的资源[5],文献[6]说明了匹配滤波器的量化位数对解扩性能的影响以及量化位数选择的依据。一般认为高斯信道下匹配滤波器选择3 bit量化比较合适,考虑到m点累加后截位的影响,本方案匹配滤波器的信号输入采用4 bit量化,实验表明:系统的运算量和捕获灵敏度都有较好的效果。

系统的预检测积分时间的选择要考虑到捕获的灵敏度和系统占用的硬件资源,积分时间越长,捕获灵敏度越高,但是占用的硬件资源就越多。

多普勒频偏覆盖范围和搜索精度同系统的预检测积分时间、部分匹配滤波器的段数 n以及FFT的点数N(N≥n)有关。设捕获的预检测积分时间为PI T,则多普勒频率搜索精度为多普勒频偏的覆盖范围为即

2.2 匹配滤波器组的设计

传统匹配滤波器的实现一般是以本地码作为匹配滤波器的抽头系数,当数字中频数据滑过时和本地码相乘后累加。抽头系数越多,乘法器和加法器也就越多,对于码速率低、码周期短的C/A码,传统匹配滤波器以消耗大量资源为代价还有用武之地,但是对于码速率高、码周期长的P码,传统匹配滤波器就显得无能为力。

为了使硬件易于实现,采用递归折叠移位寄存器实现n段折叠部分匹配滤波器组。移位寄存器的实现充分利用了基于SRAM技术的FPGA中的特殊硬件资源(如丰富的查找表(LUT)资源)。对于一个4输入的LUT,可以搭建1个1～16位的移位寄存器。移位寄存器越长,系统占用资源越小,但是,系统要求更高的时钟来实时处理ADC的采样点。为了提高FPGA的资源利用率,采用1个LUT搭建一个16位的移位寄存器。

部分匹配滤波器的单元结构如图3所示,16位递归折叠移位寄存器输入端的多路选择器判决当前时刻是移入上一级送来的信号还是移位寄存器输出端移出的信号;以本地码移位寄存器的输出作为输出端多路选择器的使能端,根据本地码为1还是0来选择两序列的相关结果,相当于匹配滤波器中的乘法器。对于某一个部分匹配滤波器,其所有的移位寄存器输出至累加模块的数据通过加法树进行累加;使用16个时钟周期分时累加1个部分匹配滤波器的相关值,并将这个相关值作为1个FFT的输入点,n段部分匹配滤波器并行执行此过程。在下一个ADC的采样点到达之前,送出n段部分匹配滤波器的 I/Q两路累加值进行 N点FFT。

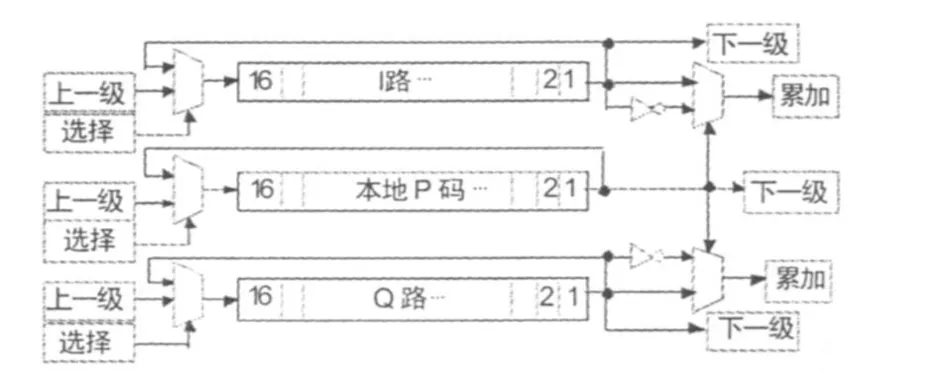
图3 部分匹配滤波器的单元结构

由以上分析可知整个匹配滤波器需要16个时钟周期处理一个m倍降采样后的点,算上读取新的数据进入匹配滤波器,宏观上就是使用17个时钟周期处理一个降采样后的数据。设 fs为系统的采样频率,则匹配滤波器组的工作频率为 fs×17/m,由于硬件结构简单,用FPGA搭建的捕获电路工作在此频率下完全可行。

对于图3所示的单元结构,匹配滤波器的抽头系数降为传统匹配滤波器的乘法器和加法器的数量也相应的减少。设整个匹配滤波器的结构为n段部分匹配滤波器,每一段部分匹配滤波器由M个如图3所示的单元组成,I、Q两路数据并行处理,则所需要占用的4输入LUT为n×M×(4+0.5)×2个(I、Q两路数据进入匹配滤波器的量化位数为4,本地P码1 bit且I、Q共用),极大地降低了FPGA的逻辑资源。

2.3 FFT模块设计

由以上匹配滤波器组的设计可知,匹配滤波器组每隔17个时钟周期输出一次部分相关值,若 N＞17,则一个N点FFT模块的吞吐率不能满足系统要求。解决方案有2种,一是使用FPGA的内部RAM来缓存匹配滤波器组的输出结果;二是增加FFT模块的数量,通过并行流水机制来处理匹配滤波器组的输出数据。考虑到整个系统的实时性和捕获速度,本方案采用后一种方式,其中FFT模块数的取值为⎿N/17」,(⎿」表示向下取整)。

2.4 检测判决模块设计

对FFT模块输出的值取模平方后,通过唐检测器来判决是否捕获到信号。唐检测器的总虚警概率为[7]

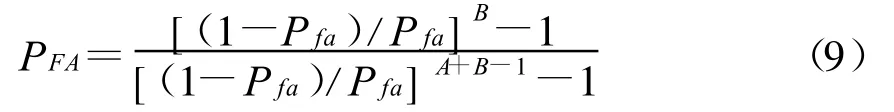
唐检测器的总检测概率为[7]

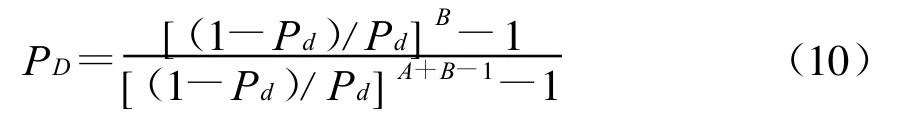
式中:Pfa为单次虚警概率;Pd为检测概率;A、B为唐检测器设定的门限值。

3 仿真及测试结果

信噪比为-34 dB、码速率10.23 MHz时的仿真结果如图4所示,对应的信号功率大约为-165 dBW。

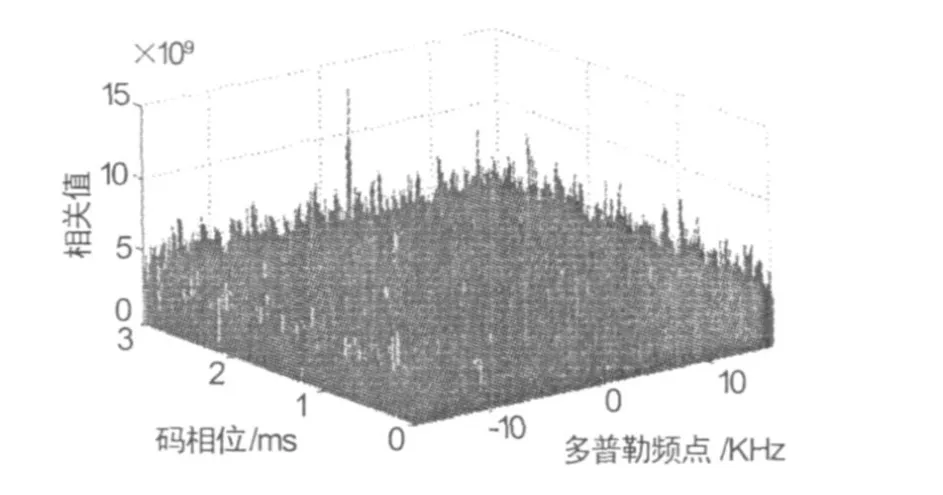
图4 SNR=-34 dB仿真结果

在硬件测试之前,先通过卫星信号模拟器产生功率为-163 dBW、码速率10.23 MHz的射频信号,对接收机前端输出的模拟中频数据用采集卡采集,经过处理后4 bit量化,作为ADC输出的数字中频数据,然后在Modelsim中仿真,结果如图5所示。

图5 功率为-163 dBW时Modelsim SE6.5仿真结果

按照设计方案进行硬件测试,在输入信号功率为-165 dBW、码速率10.23 MHz、码相位偏移±1 s、多普勒频率偏移±16 kHz的条件下,捕获时间小于10 s。

4 结 论

设计了基于FPGA的高动态P码直捕方案,所采用的是匹配滤波器组与FFT相结合的算法。方案最显著的特征是直接捕获时间短,能大大缩短P码接收机的首次定位时间;方案还具有占用硬件资源少,适合流片等特点。测试结果也表明此方案适用于新一代卫星导航系统在高动态、低信噪比环境下的P码快速直接捕获。

[1] Yang C,Vasquez J,Chaffee J.Fast Direct P(Y)-Code Acquisition Using XFAST[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of The Institute of Navigation(ION GPS 1999),Nashville,TN,1999:317-324.

[2] Jing P,Frank V G,Janusz S,et al.Fast direct GPS PCode acquisition[J].GPS Solutions,2003(7):168-175.

[3] O'Driscoll C,M urphy C C.Performance Analysis of an FFT Based Fast Acquisition GPS Receiver[C]//Proceedings of the 2005 National Technical Meeting of The Institute of Navigation,San Diego,CA.,2005:1014-1025.

[4] 张新波,张 扬,刘 田.GPS接收机P(Y)码直捕方法研究[J].电子科技大学学报,2008,37(增刊):62-65.

[5] 余建宇.基于FPGA的扩频接收机中数字匹配滤波器的设计[J].火控雷达技术,2009,38(3):30-33.

[6] 郭 南,洪福明,直接序列扩频数字匹配滤波器[J].电子科技大学学报,1996,25(5):455-459.

[7] Ward,P W.GPS Receiver Search Techniques[C]//IEEE 1996 Position,Location,and Navigation Symposium,Atlanta,GA.,1996:604-611.