大型煤气柜风荷载的风洞试验及数值模拟
张冬兵,梁枢果,陈 寅,李茂新
(1.武汉大学土木建筑工程学院,武汉 430072;2.中南电力设计院,武汉 430071;3.中冶南方工程技术有限公司,武汉 430223)
0 引 言
大型煤气柜属于特殊工业钢结构,设计时不但需要满足结构强度要求,而且需要限制结构变形满足工艺方面的要求,其中风荷载为控制因素[1]。大型煤气柜的主体为圆柱形,由于截面直径大,在风荷载作用下煤气柜筒体会产生变形,而中国规范[2-4]中圆截面结构的风荷载确定方法并不能涵盖该类结构的风荷载计算,应进行风洞试验确定风荷载。郑史雄[1]通过风洞试验研究了有周边建筑影响的大型煤气柜的表面风压并且风振系数考虑了活塞运行位置的影响,但没有涉及雷诺数效应对试验结果的影响;《工业循环水冷却设计规范》、《火力发电厂水工设计规范》[2-3]根据北大雷诺数修正的风洞试验和西安热工所现场实测数据推荐了双曲型圆截面冷却塔风荷载计算公式;赵林[5-6]、A.Zasso[7]等采用增加表面粗糙度的实验手段,获得了在低雷诺数条件下模拟高雷诺数流态特性的风洞试验条件。PietroCatalano[8]等人采用CFD方法研究了圆柱压力分布随雷诺数变化的规律。笔者采用风洞试验及数值模拟对煤气柜表面风荷载进行了研究,风洞试验中用表面粗糙度控制雷诺数效应的影响;数值模拟采用RNG k-ε湍流模型进行了实体结构和风洞试验尺寸下的相应计算,最后对试验数据、模拟结果及相关规范条文[2-4]进行了对比和分析。
1 风洞试验
1.1 风场模拟及试验方法
试验在广东省建筑科学研究院CGB-1建筑风洞中进行。该风洞为串联双试验段单回流式大气边界层风洞,大试验段长10m,宽3m,高2m,最大风速为18m/s,其工作转盘直径为2.5m,采用档板、尖塔、粗糙元装置模拟B类地貌,在模型放置中心测得的风速剖面和湍流度剖面如图1所示。

图1 平均风速和湍流度剖面Fig.1 Mean velocity and turbulence intensity profile
为了测量风洞试验参考高度处风速,在模型左前方处安装了风速管,其安装高度为0.6m,与模型测压同步测量此处的风速。该试验采用DSM3200电子扫描阀测压系统依次对所有测压点的压力信号进行扫描。脉动压力的采样时间为13.1s,每个测点的采样频率为313Hz,试验风速为8.02m/s。
1.2 试验模型及雷诺数效应控制
研究的煤气柜柜体为圆柱形,顶部为球面顶盖,直径为58.5m,柜体高97.2m,高度与直径之比为1.66,柜顶球面矢高为6.3m,球面顶部中心处有一直径为10m的圆柱形气楼,在柜体表面环向等距分布有子午向通长的32根工字钢立柱,其型号为H440×300×11×18,同时设置了环向走道及斜梯。煤气柜测压模型由有机玻璃制成并精细地模拟了表面细节形状及设施,几何缩尺比为1∶150,模型表面共布置370个测压点,其中柜体立面布置了240个测点,柜顶布置了130个测点,风洞中模型如图2所示。

图2 风洞试验模型Fig.2 Model in wind tunnel test
煤气柜结构在设计风速下雷诺数范围为9.8×107~1.4×108,风洞试验雷诺数大约为2.0×105,对于类圆截面结构,雷诺数效应是不容忽视的,采用改变模型表面粗糙度和来流湍流度等实验手段,可以在较低雷诺数的条件下可靠地模拟高雷诺数流态特性[6],已有的粗糙度处理经验能控制实验中雷诺数效应的影响,合理地模拟实际结构表面风压分布。柜顶表面采用打磨的方式进行毛面处理,并沿圆周有工字钢处径向粘贴了1cm宽的纸带来控制实验中雷诺数效应对柜顶表面风压的影响。文献[6,9]采用表面贴丝线对圆柱雷诺数效应的研究表明,当表面相对粗糙度大于5.1×10-3时流动状态将独立于雷诺数的变化。实验模型表面工字型钢用3mm×2mm矩形立柱代替,相对煤气柜的直径为7.7×10-3,同时对立柱之间的结构表面进行毛面处理。
1.3 试验数据处理
为了方便与工程应用的风荷载参数对比,风洞试验中各测点平均风压系数(体型系数)计算公式为:

式中:pi为测点i的平均风压值;ρ为空气密度;vi为测点i所在高度处来流风速;当式(1)中pi为测点i的均方根风压值时,即可得到均方根脉动风压系数。
由煤气柜表面每层同步测压点得到的阻力(顺风向)系数和升力(横风向)系数积分公式为:

式中:Ai为第i测点压力覆盖面积;θi为第i测点压力与顺风轴向夹角。
1.4 试验结果分析
以往文献很少对具有分布肋的大型圆截面结构风荷载进行系统研究[1],所以只能选取类圆截面断面形式表面风荷载的研究成果作对比。研究该结构风洞试验表面压力分布时,选用几个典型断面平均风压系数的平均值与规范中的圆截面结构体型系数进行了对比,结果如图3所示(图中‘有肋'、‘无肋'代表《火力发电厂水工设计规范》[3](简称水工规范)中基于北大试验经过雷诺数修正的有、无肋双曲面冷却塔平均风压系数、‘西热'表示基于西安热工所实测资料的双曲面冷却塔平均风压系数[2],‘规范'表示荷载规范[4]中的圆截面结构体型系数);试验中各断面的脉动风压系数[11]如图 4所示(图中 H11表示高度为11m的断面)。
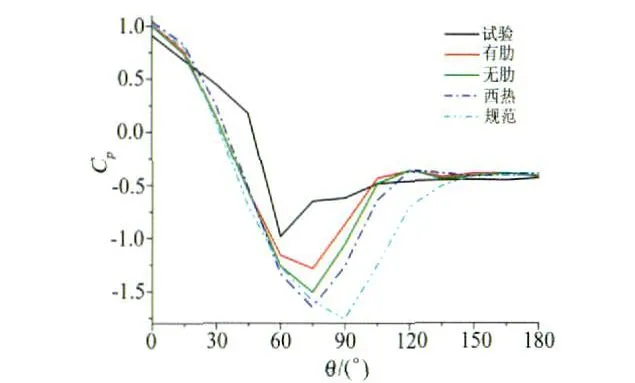
图3 平均风压系数Fig.3 Mean wind-pressure coefficient
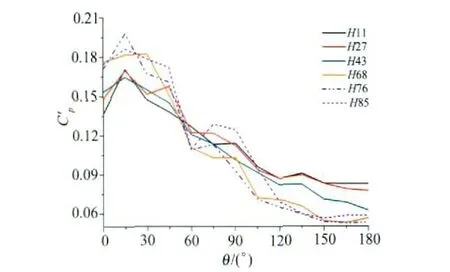
图4 均方根脉动风压系数Fig.4 RMS fluctuating wind-pressure coefficient
图3中所有规范中的体型系数,零值系数角度(θ0)在 30°~ 40°之间 ,尾流压力系数为 -0.41;荷载规范中,最小压力点(θ1)出现在 90°,尾流分离点(θb)出现在120°;水工规范推荐的3种(有肋、无肋、西热)体型系数中,θ1为70°~80°,基于北大实验的有、无肋体型系数的θb值在 100°~110°之间,基于现场实测的西热体型系数中θb在120°附近;试验结果中θ0在45°附近 ,θ1在 60°附近,θb在 75°~ 105°之间,尾流压力系数为-0.45。由于模型表面立柱的影响,通过与规范的比较,体型系数符合表面粗糙度造成的压力分布规律:来流分离区推后(θ0增大),最小压力位置提前,并且数值减小20%(与水工规范有肋时最小体型系数相比较),而尾流分离区提前;说明结构表面立柱使壁面附近产生更多湍流序列从而强烈地影响了表面压力分布,其明显有别于模拟高雷诺数流态时改变结构表面粗糙度的实验手段。
图4中脉动风压系数在60°处,75°~120°之间均出现变化点,和前述平均风压分布表现出的来流和尾流分离特征基本一致,但尾流分离区的脉动风压分布表现更为离散;图中在15°处出现的变化点,认为是由立柱造成的绕流所引起。图中各断面的均方根脉动风压系数改变量随断面高度的湍流度减小而增大,为了更清楚表示来流中湍流度的作用而引入湍流影响系数:

式中,ΔσI表示断面I上脉动风压系数改变量,mσI表示断面I上脉动风压系数的平均值;影响系数越小表示结构表面脉动压力离散程度越小。各断面的湍流度及湍流影响系数如表1所示。

表1 湍流影响系数Table 1 Influence factor of turbulent intensity
通过同步测点压力时程数据可以得到各断面的阻力和升力时程。对各风向角下各层的阻力和升力系数逐一进行谱分析,均表现出宽带谱的频谱特性,选出了具有代表性的功率谱函数如图5所示。采用试验手段模拟高雷诺数时的流场,要考虑结构表面压力分布、阻力及升力系数和斯脱罗哈数(St数)等风荷载的特性参数。当雷诺数Re>3.5×106,类圆柱结构尾流涡脱中湍流成份加大,但仍出现周期性的涡脱,结构表面的压力也会同时呈周期性变化,采用积分方式得到的阻力、升力系数的频域分析可以有效确定涡脱的卓越频率[5,10],当在实验中模拟高雷诺数的流场特性时,也会出现相应的涡脱频率[9],而实验中的升、阻力系数谱均表现出宽带特性,说明结构表面立柱产生的特征湍流强烈影响到了整个流场的流态,采用柜体直径为特征尺寸计算的雷诺数数值并不能合理地表征实际的流体流态。
2 CFD数值模拟
2.1 计算模型及网格划分
使用CFD商业软件Fluent6.3进行数值计算,采用了实体和风洞试验两种尺寸下的数值模型,并设置了合理的计算流域。考虑计算精度和资源的要求,使用混合网格策略,对结构表面及附近网格进行了加密,网格大小由内向外按比例递增同时限制最大网格长度,其中实体模型的网格划分如图6所示。在高雷诺数的数值模拟中,结构表面y+值一般较难保证在限定的范围之内,因此对结构表面附近的网格进行了细化并局部加密来满足限值的要求。
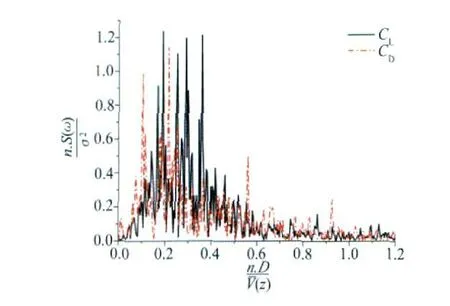
图5 升力、阻力系数谱Fig.5 PSD of lift and drag coefficient

图6 计算域网格示意图Fig.6 Sketch map of mesh scheme
2.2 边界条件的设定及壁面处理
入流面采用速度入口模拟B类大气边界层风剖面,平均风速(v)剖面按地貌指数α=0.16确定,湍流参数采用湍动能k和湍动耗散率ε组合输入,k=0.5(vI)2;ε=0.093/4k3/2/l;其中湍流强度I和湍流积分尺度l参考日本规范并结合风洞数据拟合修正得到。入流面参数均采用Fluent提供的UDF(用户自定义函数)功能来实现;出流面采用压力出流边界条件;流域顶部及两侧采用自由滑移壁面条件;结构表面及地面采用无滑移的壁面条件,由于近壁区湍流发展不充分,选用非平衡壁函数对壁面进行处理。
2.3 其 它
湍流模型采用RNG k-ε模型,对流项的离散格式采用二阶迎风格式,压力-速度耦合方程的解法采用SIMPLE算法[12]。
3 数值模拟结果
实际结构和风洞试验计算雷诺数分别约为1.0×108,2×105,两种工况数值计算的平均风压系数(体型系数)在图7分别表示为Re8,Re5。图中对比了同一风向角下各断面数值模拟、风洞试验的平均风压系数,图中为柜体表面不同高度同一方位角上点的平均风压系数;从图中曲线Re8看出,在来流分离点前数据稳定并与试验值一致;最小压力值位置与试验值相位角相差约10°,但数值较为一致,可以认为表面立柱对风压分布的影响所致;尾流分离区位置与试验值一致;尾流压力系数值与试验值相差不足10%。从图中工况Re5看出,最小压力值在图中并不突出而且较试验值小近30%;尾流压力系数值比试验值约低10%。通过分析认为:实体结构数值模拟能准确得到结构表面来流分离点前及尾流分离后的平均风压数值,平均风压的分布特征也能准确地表征,但在分离区内的风压数值与试验值还有一定的差异;由于结构表面工字钢立柱和湍流度对流场的影响,不同量级雷诺数的数值模拟的平均风压系数在分离区有一定差别,但在来流面及尾流区的数值相差不足10%。
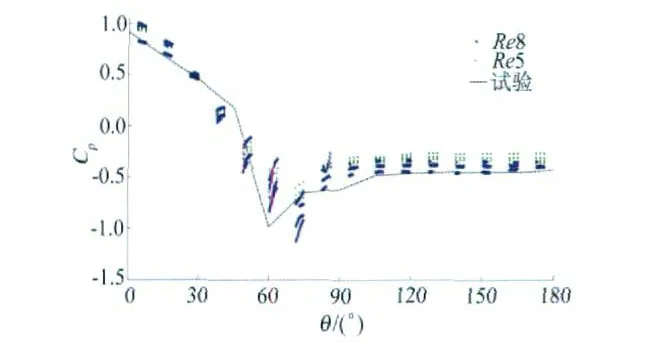
图7 平均风压系数Fig.7 Mean wind-pressure coefficient
柜体中间高度处平面的流线如图8所示,图中尾流旋涡在柜体两侧均为不对称分布,尾流区邻近柜体处流线平缓并没有旋涡中心出现;工况Re8中离柜体较远处可以看到明显三维绕流的影响,而且旋涡分布更显复杂;不同量级雷诺数下模拟的流场分布存在差别,这是否是引起柜体分离区平均风压分布差别的原因还有待于相应的实测数据对数值模拟结果及试验中雷诺数效应控制方式的验证。
实际结构数值模拟的流迹显示如图9所示,图中绕柜体的流动结构复杂,可以看到气流的冲撞、分离、涡旋和回流等流相。绕柜体上方的流线向下卷起涡旋,柜体中央来流的流线受表面立柱影响产生涡旋,并在柜体背后竖向的涡旋交织在一起,因此柜体流场自来流分离区开始就高度紊乱,而且经由立柱产生的复杂绕流影响了整个流场的流动特性。
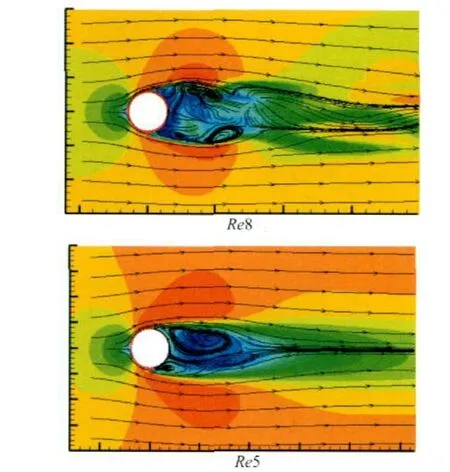
图8 流线分布图Fig.8 Streamlines of mean velocity distributions

图9 局部流线图Fig.9 Local map of path lines
4 结 论
(1)结构表面分布的立柱对来流分离、尾流分离位置及分离区的最小风压值影响较大;由于结构表面立柱的影响,结构断面的升、阻力系数谱表现出明显的宽带频谱特征;来流中湍流度会影响结构表面风压分布;
(2)采用雷诺平均的RNG k-ε湍流模型基本上能准确地模拟结构平均风压分布,在高雷诺数下煤气柜表面工字钢立柱附近及分离区的风压计算结果与试验值还有一定的差别,但可以与风洞试验结果一起对工程设计的风荷载提供参考;数值模拟能直观地显示流场,可以帮助人们了解结构绕流场复杂的流动特征;
(3)不同量级雷诺数下数值计算能反映雷诺数效应的影响,但同风洞试验中控制雷诺数效应的试验手段都需要相应结构的实测数据做检验和修正。
[1] 郑史雄.大型储气结构设计风荷载的确定[J].福州大学学报(自然科学版),2005,33(supp):90-94.
[2] GB/T 50102-2003,工业循环水冷却设计规范[S].北京:中国电力出版社,2003.
[3] DL/T 5339-2006,火力发电厂水工设计规范[S].北京:中国电力出版社,2006.
[4] GB50009-2001,建筑结构荷载规范[S].北京:中国建筑工业出版社,2002.
[5] 李鹏飞,赵林,葛耀君,等.超大型冷却塔风荷载特性风洞试验研究[J].工程力学,2008,25(6):60-67.
[6] 刘天成,赵林,丁志斌.圆形截面冷却塔不同表面粗糙度时绕流特性的试验研究[J].工业建筑,2006,36(增刊):301-305.
[7] ZASSO A,GIAPPINO S,MUGGIASCA S.Wind tunnel study of a cone-like shaped roof Reynolds number effects[J].Journal of Wind Engineering and Industrial Aerodynamics,2006,94:431-444.
[8] PIETRO C,WANG Meng,GIANLUCA I,et al.Numerical simulation of the flow around a circular cylinder at high Reynolds numbers[J].International Journal of Heat and Fluid Flow,2003,24:463-469.
[9] 李会知,樊友景,吴义章,等.不同粗糙表面的圆柱风压分布试验研究[J].工程力学,2002,19(2):129-132.
[10]李加武,林志兴,金挺.压力积分法在桥梁断面雷诺数效应研究中的应用[J].振动工程学报,2006,19(4):505-508.
[11]希缪◦E,斯坎伦◦R H著.刘尚培,项海帆,谢霁明译.风对结构的作用-风工程导论[M].上海:同济大学出版社,1992.
[12]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.

