主动来流条件类平板断面气动力荷载效应分析

潘 韬,赵 林,曹曙阳,葛耀君,S.Ozono

(1.同济大学土木工程防灾国家重点实验室,上海 200092;2.Department of Physics,Miyazaki University,Miyazaki 889-2155 Japan)

0 引 言

对于主跨达到800m斜拉桥和1500m悬索桥等超大跨度桥梁,基于精细化研究思路描述气动力荷载的相关参数(包括静风力系数、颤振导数和气动导纳),风洞试验识别理论和技术方法的研究已成为大跨度桥梁抗风性能研究的关键技术,其中静风力系数和颤振导数识别工作,国内外已取得较好的研究进展,而与结构气动力作用时频转换和空间相关性密切联系的随机抖振理论尚未突破流线型断面的理论框架,尤其是关于积分尺度荷载效应和来流湍流及特征湍流非线性效应的研究基本上处于空白状态。

对于随机抖振气动力荷载作用模式及规律的相关研究不足主要表现在：对于描述特定桥梁断面,对于不同来流频率成份有选择放缩的气动力准定常修正项的气动导纳函数,工程应用中常假定气动导纳的上限值为1、下限值为薄平板断面的Sear函数,而基于气动导纳这两种取值的计算结果可以导致1倍左右的计算误差;由于导纳识别算法推导过程引入诸多近似假定和风洞试验设备测试精度及来流输入条件,如：积分尺度等参数无法准确控制等问题,相同气动外形桥梁断面所识别的导纳函数差别较大,且难于再现经典刚性机翼断面Sears函数解析结果,多数风洞试验气动导纳识别结果不具有明确的物理意义,难于验证其识别结果的有效性和合理性[1-4]。

针对上述问题,由改善大气边界层物理风洞来流模拟条件入手,利用日本宫崎大学多风扇主动控制风洞和高精度测力天平,初步探讨了不同频率和波长正弦来流作用下类平板断面气动力荷载变化规律。

1 试验条件和工作准备

1.1 风洞条件与试验设备

宫崎大学主动风洞是由99个独立送风机组成的直流式、多段可拼接主动控制式风洞,可有效地模拟来流平均风和湍流度剖面效应,合理再现不同积分尺度来流正弦风波和宽频脉动风时程[5-7]。试验段宽2.538m×高1.804m,风速可调范围为0～15m/s,正弦风速变动上限9m/s来流风速时风速,变化幅值为±3.5m/s,最大波动频率为5Hz。节段模型气动力测量装置采用三分量高精度小量程动态高频测力天平,天平两个侧向力(Fx,Fy)量程范围为±20N,水平扭矩(Mz)为±2N◦m,测量精度可达1‰。试验室配备了同步采集监控与触发装置,可实时再现脉动风加载与模型气动力同步测量过程。宫崎大学11×9多风扇主动风洞如图1所示。类平板模型及测力系统安装情况如图2所示,试验模型重量为360g,安装后实测弱轴频率为24Hz,强轴频率为44Hz,对于该试验模型固有频率远大于正弦来流风的主导频率(0.2～4.0Hz),整个系统满足动态高频测力试验的需要。

1.2 正弦来流湍流度定义

对于正弦来流条件下湍流度定义为：

式中,σ表示正弦来流风速的均方根值,U(z)表示正弦来流平均风速。

1.3 试验工况安排

为了系统地比较不同来流参数对作用在模型上气动力影响规律,对正弦来流加载条件,逐一比较来流平均风速、波动幅值和频率、湍流度和积分尺度等参数组合情况的作用效果,表1列举了不同正弦来流参数取值概况。

2 正弦来流模拟与气动力倍频效应

主动风扇加载的正弦脉动风随吹风距离存在明显的衰减关系,这种衰减表现在脉动风幅值的变化,而对周期性的脉动频率影响不大,同时随加载频率的高低存在特殊的气动力荷载倍频放大效应。

图1 宫崎大学11×9多风扇主动风洞Fig.1 11×9 multiple fan active control wind tunnel in Miyazaki University

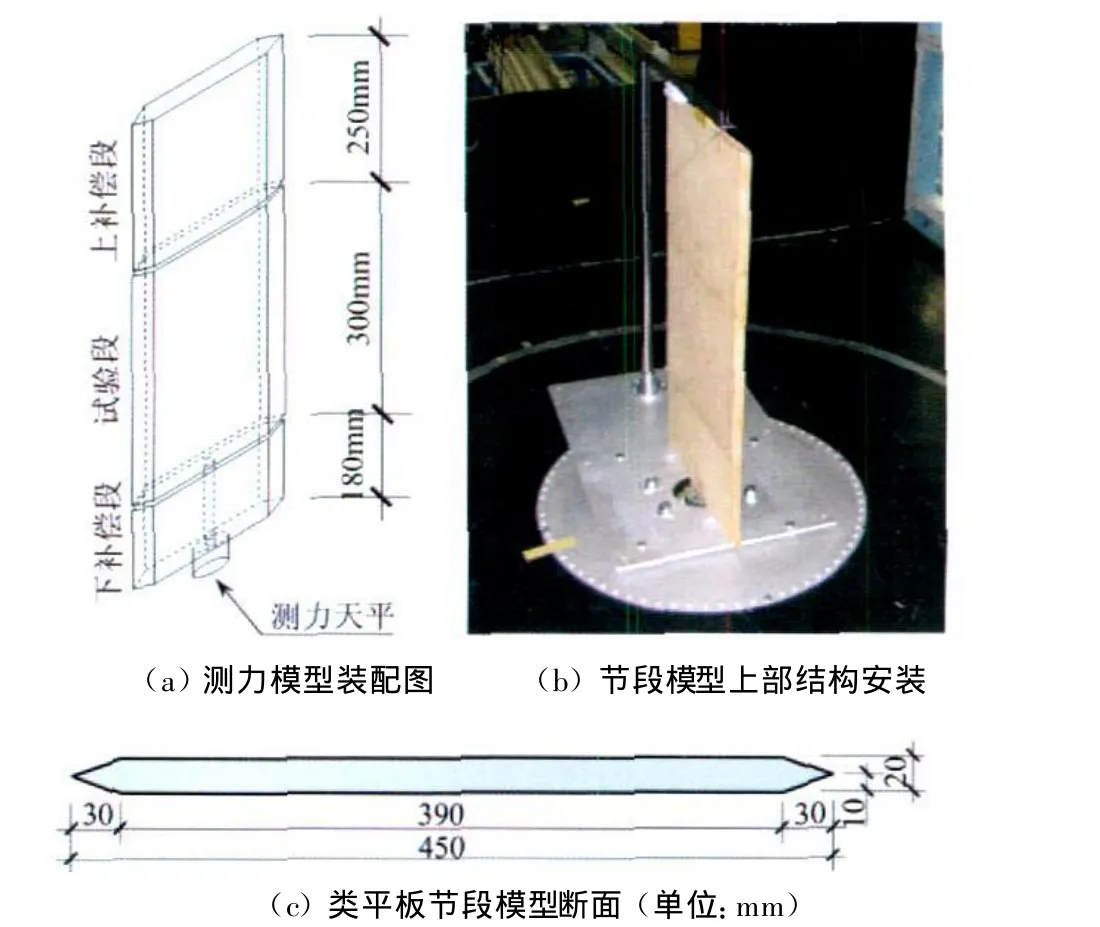
图2 类平板模型及测力系统安装情况Fig.2 Installation of model and measurement system in wind tunnel

表1 不同正弦来流参数组合情况列表T able 1 Combinations list for different sinusoidal flow parameters

2.1 低频正弦来流模拟

风洞入口段加载信号：U=6m/s、A=3m/s、f=0.6Hz=10m;试验段实测信号 ：U=6.38m/s、A=1.19m/s、f=0.60Hz=10.13m 、=0.38m 、Iu=13.24%、Iw=0.51%。

u向脉动风相比w向脉动风占有绝对优势,脉动能量之比约1200∶1关系;主要试验现象表现为u向脉动风单一卓越频率对应顺风向和横风向气动力各单一卓越频率。

2.2 高频正弦来流模拟

风洞入口段加载信号：U=6m/s、A=3m/s、f=2Hz、=3m;试验段实测信号：U=6.43m/s、A=0.43m/s、f=2.00Hz=3.05m 、=1.44m 、Iu=4.74%、Iw=0.78%。

u和w向脉动风存在多阶对应峰值频率,脉动能量之比约40∶1关系;主要试验现象表现为u向脉动风单一卓越频率对应顺风向和横风向气动力各多阶卓越频率。

2.3 倍频效应数值模拟

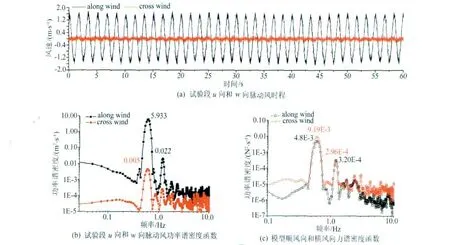
图3 低频正弦脉动风加载流场与模型气动力效应Fig.3 Low frequency sinusoidal fluctuating wind field and the model aerodynamic load effect

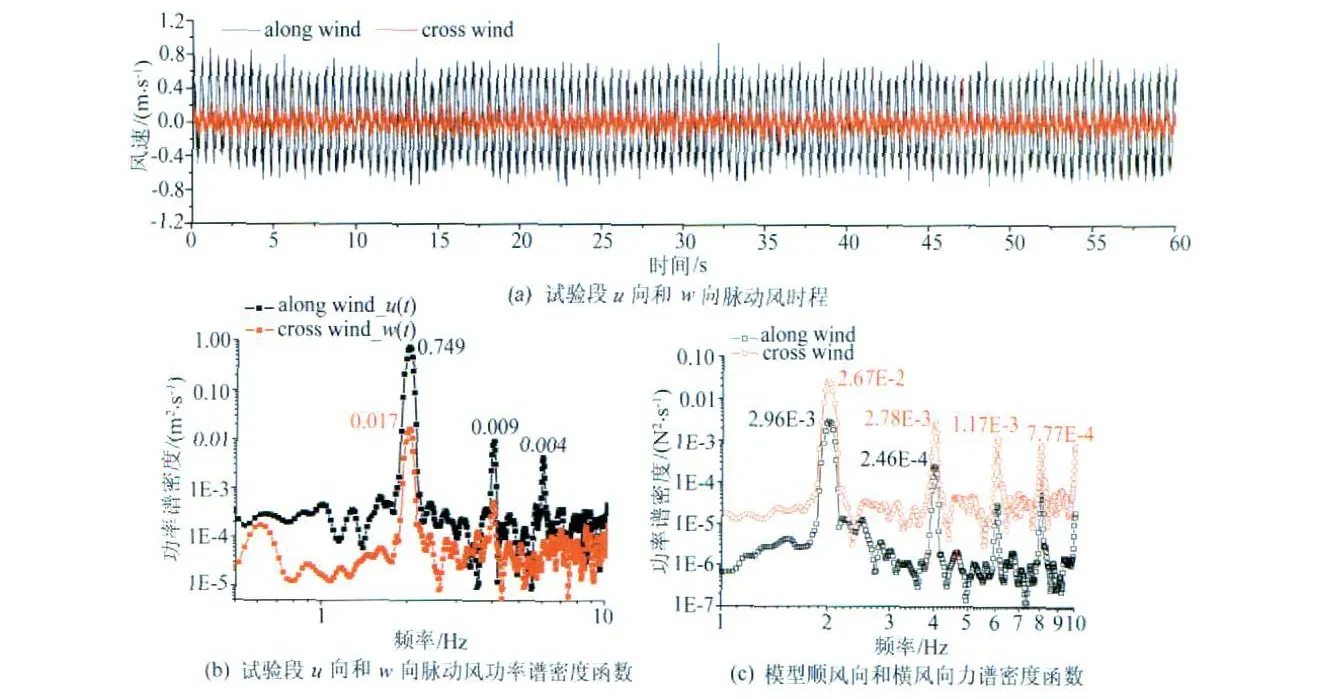
图4 高频正弦脉动风加载流场与模型气动力效应Fig.4 High frequency sinusoidal fluctuating wind field and the model aerodynamic load effects

曹丰产[8]采用CFD方法计算分析正弦风波来流条件对于桥梁断面气动力作用模式及特点过程中,发现了气动力倍频放大效应,计算模型数值边界纵横向尺度为桥梁断面宽度的12～14倍。对于较为流线型的南京三桥主梁断面(宽高比11.55∶1),1.0Hz加载脉动风波在气动力荷载谱中出现了幅值为一阶主导频率谱密度幅值的约0.1倍倍频放大(如图5所示),该结果与图4(c)类平板模型2.0Hz加载频率结果类似;对于偏钝体气动外形的越南RachMieu大桥(宽高比7.10∶1),0.6Hz加载脉动风波出现了幅值为一阶主导频率谱密度幅值约0.5～0.1倍的多阶倍频放大,倍频效应更加明显。初步确认倍频产生原因为正弦加载脉动风波传递至数值边界壁面后产生的反射共振效应。由此推论大气边界层物理风洞亦不可避免同样会出现此类似效应,导致在较高的共振反射频段出现气动力荷载放大效应,处于该频段的结构风荷载效应存在偏大趋势。

图5 南京三桥正弦脉动风加载模型气动力效应Fig.5 Model of third bridge in Nanjing Yangtze River in sinusoidal fluctuating wind field and aerodynamic load effects

图6 RachMieu大桥正弦脉动风加载模型气动力效应Fig.6 Model of RachMieu bridge in sinusoidal fluctuating wind field and aerodynamic load effects

3 试验参数分析

3.1 离散频率线性迭加分析

由正弦来流脉动风模拟可知,在较高的来流脉动风频段存在明显的倍频放大效应,这种倍频效应会导致部分来流脉动风频段气动力荷载效应线性迭加原理不成立,为了由单频风波进一步分析宽带脉动风气动力效应,需确认气动力荷载线性迭加原理的有效频段。如图7所示,针对多风扇主动风洞模拟的宽频输入(实心矩形点连线),可以由一系列不同频率和波动幅值的正弦风波在多个频段上模拟合成(空心多边形点连线),需要指出的是由于在高频段(＞4Hz)选取的正弦主导频率较少,因此其和值与宽频风谱存在一定差距,因此分析中只取频率2～4Hz范围。如果输入单频风波能量(同时包括u向和w向风谱峰值)与宽频脉动风较为一致,模型顺风向和横风向气动力单频和宽频对应荷载能量吻合程度亦较高。分析过程从侧面证实：(1)对于该项研究中的类平板断面,在2～4Hz频段范围单频风波近似可满足荷载效应线性迭加原理;(2)为获得与真实情况一致的气动力荷载效应,有必要增强主动风洞横风向(w向)脉动特性模拟。

3.2 积分尺度荷载效应

湍流积分尺度在结构风荷载分析中具有不可忽略的意义,积分尺度的大小决定了脉动风对结构的影响范围。通常认为：如果脉动涡旋大到将某一结构包含在内,则脉动风在结构各个部位引起的动荷载会叠加,反之,动荷载可能相互抵消;即脉动风积分尺度越大,作用在结构上的气动力荷载越明显。对于此问题,可以作如下分析。如表2比较3种不同风速和波动幅值正弦来流条件,3种情况具有相同的来流脉动频率和相近的湍流度。按传统的认识,可初步判断：工况Sin-1条件积分尺度最小,标识脉动风能量的波动幅值亦最小,可得出该工况来流条件作用于模型的气动力效应会最小,工况Sin-2和Sin-3气动力荷载依次增大。对比主动风洞试验分析结果(如图8,风谱和力谱3种工况能量谱峰值比),发觉结论刚好相反,这意味着大的积分尺度不一定对应较大的荷载效应,在宽带湍流场中,亦有相同的结论[9];传统理论考虑了平均涡旋所引起的湍流强度的不同,但由于结构本身会对湍流各频率成分所引起的荷载效应有选择性的放大或者缩小。积分尺度与模型宽度之比越大,气动力的非定常性越弱,当积分尺度足够大,气动力将为准定常或完全定常。

表2 不同积分尺度来流条件参数Table 2 Wind field parameters with different integral length

3.3 湍流度荷载效应

在众多试验工况中选择两类工况,第一类如表3所示,第二类如表4所示。第一类为小湍流度条件(Iu≤5.0%),第二类为大湍流度条件(5.0%≤Iu≤30.0%),除风速波动幅值和湍流度外其它参数相近。

分析模型气动力荷载可知,对于上述两类工况条件,顺风向和横风向气动力荷载均随来流湍流度的增加而显著递增,顺风向气动力(阻力)谱峰值大小与来流湍流度大小基本成正比(如图9);横风向气动力(升力)变化比例受来流湍流度绝对数值影响较大,表现为与来流湍流度递增而加速荷载放大变化,如小湍流条件谱峰值比：L3/L2/L1=2.35/1.70/1.00,而大湍流条件峰值比：L3/L2/L1=9.39/4.56/1.00,体现出气动力变化的二次项附加荷载效应特点(如图10)。

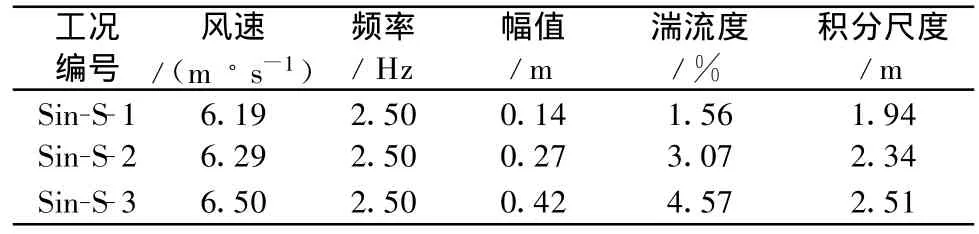
表3 不同湍流度来流参数(小湍流度条件)Table 3 Wind field parameters with different turbulence intensity(small intensity)

图9 小湍流条件湍流度效应对于气动力影响比较Fig.9 Comparison of turbulence intensity impact on aerodynamic force under small intensity condition

图10 大湍流条件湍流度效应对于气动力影响比较Fig.10 Comparison of turbulence intensity impact on aerodynamic force under large intensity condition

表4 不同湍流度来流参数(大湍流度条件)Table 4 Wind field parameters with different turbulence intensity(large intensity)

4 结 论

通过主动控制来流风洞将宽频随机脉动风分解为系列正弦风波组合,在验证气动力荷载效应在特定频段内可线性迭加原理的基础上,分析了不同来流风波参数对于类平板断面的荷载效应机制,表明部分节段模型风洞试验现象已难以由传统随机抖振力理论作出合理的解释,揭示了作用在典型二维结构上气动力荷载效应的复杂性。结合上述问题,有必要在随后的研究中,将研究对象由类平板断面扩展至更多的具有显著钝体性质的结构断面,进一步分析气动力荷载效应作用机制及规律。

[1] 秦仙蓉,顾明.桥梁结构气动导纳识别的随机子空间方法[J].同济大学学报,2004,32(4)：421-425.

[2] 赵林,葛耀君,李鹏飞.气动导纳函数互谱识别方法注记[C].第十三届全国结构风工程学术会议论文集,辽宁,大连,2007,698-707.

[3] 周斌.基于Fluent大涡模拟方法的桥梁断面气动参数识别[D].同济大学硕士学位论文,2009.

[4] 李鹏飞.脉动风特性及其对桥梁主梁断面的抖振作用研究[D].同济大学硕士学位论文,2007.

[5] NISHI A,KIKUGAWAH,MATSUDA Y,et al.Turbulence control in multiple-fan wind tunnels[J].Journal of Wind Engineering and Industrial Aerodynamics,1997,67&68：861-872.

[6] NISHI A,KIK UGAWA H,MATSUDA Y,et al.Active control of turbulence for an atmospheric boundary layer model in a wind tunnel[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,83：409-419.

[7] CAO S Y,NISHIB A,KIKUGAWAC H,et al.Reproduction of wind velocity history in a multiple fan wind tunnel[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90：1719-1729.

[8] CAO F C,GE Y J,ZHU L D,et al.Investigation on the different regularities in aerodynamic admittances of bridge decks based on CFD approach[C].The 4th International Conference on Advances in Wind and Structures(AWAS'08)Jeju,Korea,M ay 29-31,2008.

[9] 潘韬,赵林,曹曙阳,等.多风扇主动控制风洞类平板断面抖振力识别研究[J].振动与冲击,2010,29(6)：178-183+230.