超超临界汽轮机转子X12CrM oWVNbB10-1-1钢棘轮效应的试验研究

赵 鹏, 轩福贞, 涂善东

(华东理工大学 承压系统安全科学教育部重点实验室,上海 200237)

在非对称应力循环载荷作用下,由于平均应力的存在,材料的非弹性变形将产生循环累积,这种现象称为材料的棘轮效应.棘轮效应广泛存在于压力容器和管道、轮轨接触疲劳、紧固连接和密封技术等工程问题中,是工程设计中必须考虑的重要因素[1].然而,早期对超超临界电厂高温部件寿命和可靠性的研究主要关注疲劳和蠕变机制及两者的交互作用,往往忽略了棘轮效应的影响,给机组的长周期可靠运行带来了不安全因素.在高温、高压下,材料和结构的损伤往往来源于多种机制,且各种机制之间并不是孤立的,常常有显著的交互作用[2-3].因此,为保证机组的稳定运行,在进行寿命和可靠性分析时,必须考虑棘轮、蠕变和疲劳之间存在的交互作用.

近20年,国内外对材料的棘轮效应进行了大量的试验及理论研究[4-5],但以往对棘轮效应的研究主要集中于棘轮效应本身的试验研究和本构模型构建方面,对材料的棘轮与蠕变/疲劳等各种机制的交互作用及其对寿命的研究却鲜见报道.因此,本文探讨了超超临界汽轮机转子X12CrMoWVNbB10-1-1钢的棘轮和蠕变的交互作用及其对寿命评估的影响.

1 试验方法

试验材料X12CrM oWVNbB10-1-1钢直接从超超临界机组汽轮机转子上切割获得.在高温电子CSS-3905蠕变试验机上由载荷控制进行棘轮效应试验,试验温度为600℃,环境为试验室大气,波形为梯形波,在峰值应力处保持,具体试验参数见表1.共进行了3种类型的试验,其中保持时间为零和无穷大时的试验分别代表纯疲劳试验和蠕变试验,而其他改变保持时间的试验是为了研究材料在蠕变-疲劳载荷下的棘轮效应.

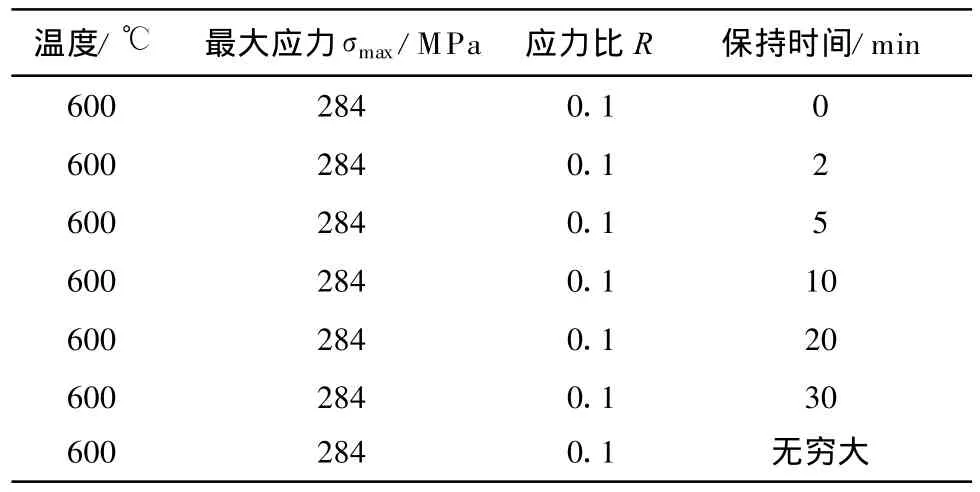
表1 棘轮效应试验参数Tab.1 Experimenta l parameters for ratchet ef fect test

定义棘轮应变为:

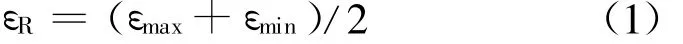
式中 :εR 代表棘轮应变 ;εmax和 εmin分别为每一个循环中的应变最大值和应变最小值.

棘轮应变率定义了2种形式:一种形式为与循环有关的dεR/d N,即每一个加载循环下棘轮应变的增量;为了与纯蠕变行为进行比较,文中还定义了另一种与时间有关的dεR/d t,即一个单位时间下棘轮应变的增量.

2 结果与讨论

2.1 棘轮行为

图1为不同保持时间下X12CrMoWVNbB10-1-1钢的棘轮应变随循环次数的变化图.由图1可见,棘轮效应随循环次数的变化与一般的蠕变应变随时间的变化趋势相似,可以分为3个阶段:①瞬态阶段,棘轮应变速率范围随着循环的进行而减小;②稳态阶段,棘轮应变速率基本保持为一常数,本文把处于此阶段的应变速率定义为稳态棘轮应变速率;③加速阶段,棘轮应变速率迅速增大,致使试样快速失效.由此可知,随着保持时间的延长,材料棘轮应变的稳态阶段越短,并且越早进入加速阶段.

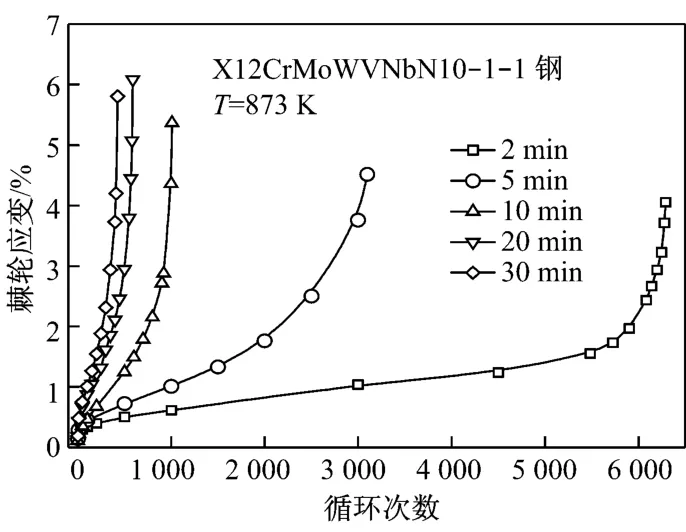
图1 保持时间对X12C rMoWVNbB10-1-1钢棘轮行为的影响Fig.1 Influence of hold time on ratcheting behavior of X12C rMoWVNbB10-1-1 steel

图2(a)为加载频率对X12C rMoWVNbB10-1-1材料稳态棘轮应变速率的影响,为了与蠕变行为进行比较,图2(b)列出了材料在稳态阶段内单位时间应变速率随频率的变化,其中蠕变的频率定义为0.由图2可知,材料的应变速率随着频率的增加而逐步降低,这表明加卸载阶段会降低材料的棘轮效应.随着频率的增加,加卸载所占分数也会逐步增加,从而会逐步降低材料的棘轮效应.Ma等[6]的研究表明,加载阶段产生的滞弹性行为会降低材料的循环蠕变(棘轮),从而造成循环蠕变(棘轮效应)的减速现象.Sawada等[7]研究发现,由于P92钢回火组织中板条结构非常复杂,且板条界面的移动与时间有关,从而使P92钢表现出明显的滞弹性行为.本文所研究的X12CrMoWVNbB10-1-1材料和P92同属于9%～12%Cr钢,同样具有复杂的回火板条结构,这表明滞弹性可能是造成棘轮效应减速的主导机制.

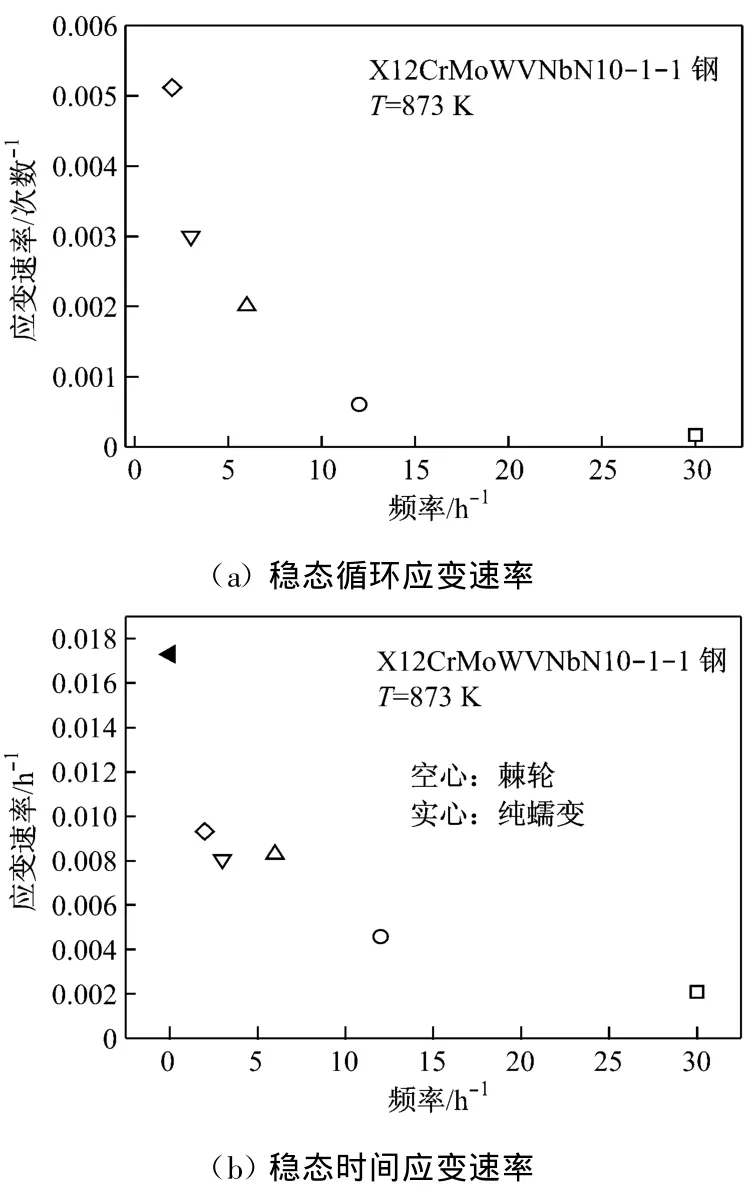
图2 加载频率对X12CrMoWVNbB10-1-1材料稳态循环应变速率和稳态时间应变速率的影响Fig.2 Influence of loading frequency on cyclic steady strain rate and unit time steady strain rate of X12C rM oWVNbB10-1-1 steel

2.2 寿命评估

图3为X12CrM oWVNbB10-1-1材料的稳态时间应变速率与时间寿命的关系.由图3可见,在双对数坐标下,在保持时间≥5 min的情况下,材料的稳态应变速率和寿命呈良好的线性关系,不管是蠕变数据还是棘轮数据,都处于同一条直线上,符合蠕变寿命评估公式Monkman-Grant关系,这表明在较大的保持时间下,材料的寿命由与时间相关的静态蠕变机制控制.这与本文的疲劳试验结果相符,在纯疲劳情况下,X 12CrM oWVNbB10-1-1材料的循环寿命＞6×104次,表明在本研究范围内材料的疲劳损伤很小,材料的寿命主要由蠕变损伤控制.但对于保持时间为2m in的情况,棘轮应变和寿命的关系明显不符合上述机制,说明在低保持时间下材料可能具有不同的损伤机制.

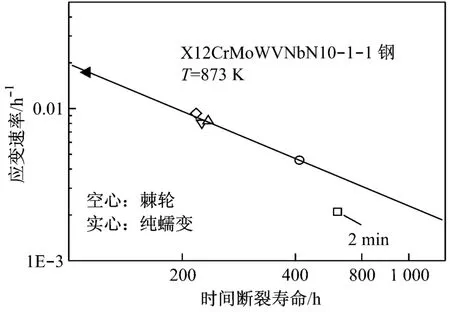
图3 X12CrM oWVNbB10-1-1材料稳态时间应变速率与时间寿命的关系Fig.3 Unit time steady strain rate vs.time life of X12C rM oWVNbB10-1-1 steel

图4是X12CrM oWVNbB10-1-1材料的棘轮及蠕变应变随时间寿命分数的演化曲线.从图4可以看出,在具有较大保持时间(＞2 min)的循环载荷中,棘轮应变随归一化寿命的演化曲线基本上与材料的纯蠕变曲线重合.结合图3的结果发现,在较大保持时间内,棘轮应变本质上与蠕变行为没什么差别,材料的寿命由棘轮应变演化控制,也就是由蠕变损伤控制.然而,在保持时间为2 min的情况下,材料棘轮应变的演化与其他时间的明显不同,似乎有某种机制抑制了材料在低保持时间内棘轮效应的产生.为了深入探讨保持时间对棘轮应变的影响,必须细致分析材料的棘轮组成.

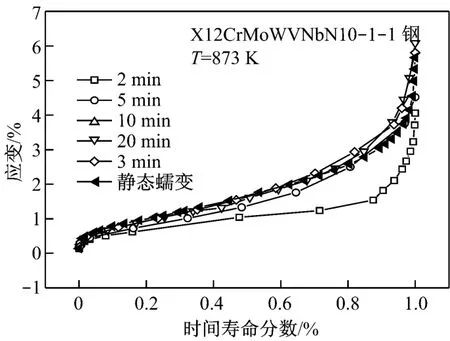
图4 归一化时间寿命下X12C rM oWVNbB10-1-1材料的棘轮及蠕变应变演化曲线Fig.4 Evolution of ratcheting and creep strain in terms of normalized time life

在具有保持时间的循环载荷下,材料的棘轮应变εR可以分为两部分:一是纯交变载荷下产生的非弹性应变循环累积εR1;二是在保持时间段内产生的蠕变应变循环累积εR2.从图5可以看出,保持时间会影响纯交变载荷下产生的非弹性应变循环累积εR1,当保持时间≥5m in时,纯交变载荷下产生的棘轮效应εR1会出现安定现象(图5中只列出了保持时间为2min和 30min的结果.5m in、10m in和 20 min的结果与30 min的类似).而当保持时间为2 min时,材料的棘轮应变率ε◦R1在经历过一个瞬态阶段后,几乎保持稳定,并不会出现安定现象.交变载荷下产生的εR1和在保持时间内产生的εR2存在交互作用,从而抑制了棘轮效应的产生,进而导致棘轮应变在低保持时间下出现不同的演化形式.

Date等[8]的研究表明,拉伸棘轮效应(即本文中在交变载荷下产生的棘轮应变εR1)对寿命的降低程度远大于同等数量的预应变.而Yang等[9]的研究同样表明,在传统的蠕变或疲劳中材料的断裂寿命与稳态蠕变速率或循环塑性应变之间的关系无法适用于存在棘轮(即本文的εR1)和疲劳交互作用的情况下.对上述前人研究的分析发现,棘轮应变εR1的损伤不能简单的通过累积应变来度量.虽然在保持时间段内产生的蠕变应变循环累积εR2的损伤是与时间有关的,但是由于蠕变变形累积和塑性应变累积属于不同性质的损伤,因此它们对材料寿命的影响具有不同的机制.而应变εR1的累积只能度量棘轮效应εR1的部分损伤,无法反映其对损伤循环特性的影响.因此,笔者提出采用应变εR1和循环塑性应变之和来度量每个循环的棘轮应变εR1损伤,这样既可以反映棘轮效应的时间相关特性,又可以反映棘轮损伤的循环特性.

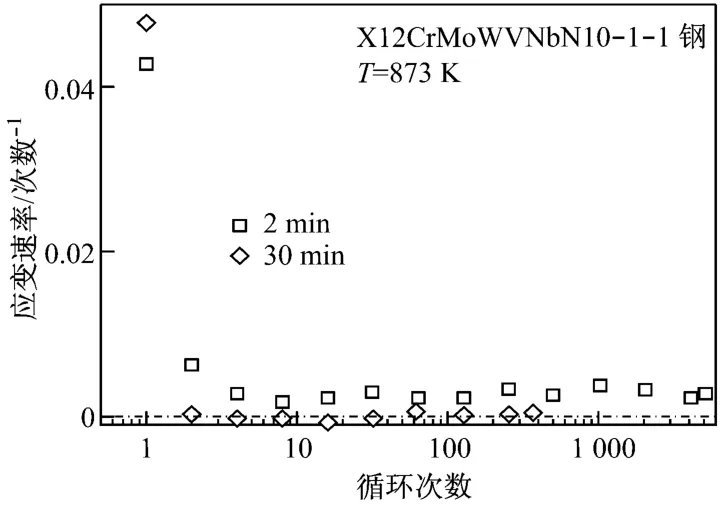
图5 保持时间对X 12CrMoWVNbB10-1-1材料在交变载荷下产生的棘轮应变率R1的影响Fig.5 Influence of hold time on unit time strain rate under cyclic loading conditions

上述结果表明,由于保持时间会影响纯交变载荷下产生的非弹性应变循环累积εR1,在低保持时间和高保持时间区内,材料具有不同的损伤机制.因此,在进行材料的寿命评估时,必须进行分区分析,将试验数据分为高保持时间和低保持时间区,在不同区域采用不同的损伤参量.由图6可知,利用分区分析的方法可以进行精确的寿命预测.

3 结 论

(1)X12CrM oWVNbB10-1-1材料的棘轮效应表现出明显的时间相关特性.材料的稳态棘轮应变速率低于同等条件下的蠕变速率,显现出棘轮减速现象,并且随着加载频率的增加,材料的稳态棘轮应变速率逐渐减小.

(2)X12C rMoWVNbB10-1-1材料在高保持时间和低保持时间内具有不同的棘轮演化行为,这种区别来源于不同的棘轮组成.在低保持时间内,由于棘轮应变εR1的形成,会抑制材料在保持时间内产生的蠕变应变循环累积εR2.

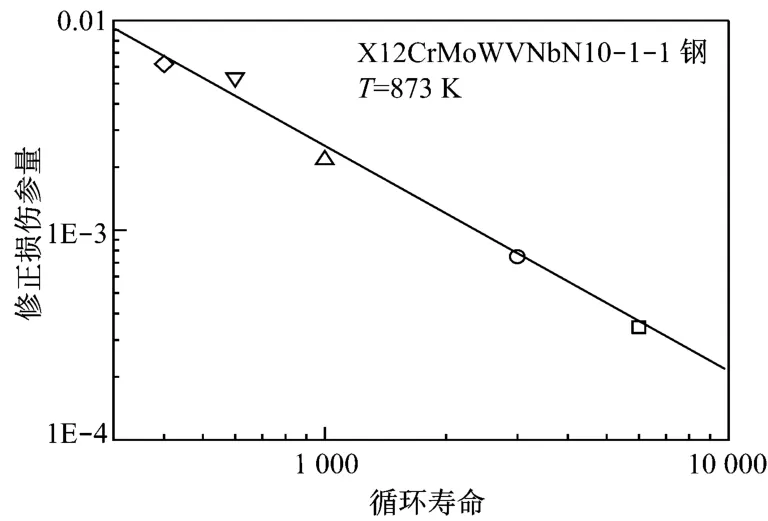
图6 X 12CrMoWVNbB10-1-1材料的修正损伤参量和循环寿命的关系Fig.6 Modified damage parameter vs.cycle life of the steel for X 12CrMoWVNb B10-1-1 steel

(3)棘轮应变εR2本质上与纯蠕变行为相同,其对材料寿命的影响可以归类为与时间有关的蠕变损伤.而对于棘轮应变εR1,提出了采用εR1和循环塑性应变之和来度量其损伤.针对不同的损伤机制,利用分区分析的方法可以进行精确的寿命评估.

[1] 陈旭,焦荣,田涛.棘轮效应预测及其循环本构模型研究进展[J].力学进展,2003,33(4):461-470.

[2] 涂善东.高温结构完整性原理[M].北京:科学出版社,2003.

[3] 李立人,陈玮,盛建国,等.锅炉受压元件的高温蠕变-疲劳寿命设计计算方法[J].动力工程,2009,29(5):409-416.

[4] OHNO N.Recent progress in constitutive modeling for ratchetting[J].Materials Science Research International,1997,3(1):1-9.

[5] KANG G Z.Ratchetting:recent p rogresses in phenomenon observation,constitutive modeling and application[J].International Journal of Fatigue,2008,30(8):1448-1472.

[6] MA Z Y,TJONG SC,WANG Z G.Cyclic and static creep behavior of A l-Cu alloy composite reinforced with in-situ A l2O3and TiB2particulates[J].Materials Science and Engineering:A,1999,264(1/2):177-187.

[7] SAW ADA K,KIMURA K,ABE F.Mechanical response of 9%Cr heat-resistant martensitic steels to abrupt stress loading at high temperature[J].Materials Science and Engineering:A,2003,358(1/2):52-58.

[8] DATE S,ISH IKAWA H,OTAN IT,eta l.Effect of ratcheting deformation on fatigue and creep-fatigue life of 316FR stain less steel[J].Nuclear Engineering and Design,2008,238(2):336-346.

[9] YANG Zhian,WANG Zhirui.Effect of p restrain on cyclic creep behaviour of a high strength sp ring steel[J].Materials Science and Engineering:A,1996,210(1/2):83-93.