基于灰色马尔可夫链模型的航空货运量预测研究＊

文 军

（中国民用航空飞行学院 航空运输管理学院 广汉 618307）

0 引 言

航空货物运输是一个复杂的社会经济系统，受到社会、经济、自然等多种因素的综合影响［1－2］.例如，航空货运量与固定资产投资、飞机的使用率、航空运输生产组织、季节更替、其他运输方式的存在等因素都有关系，而每一因素的影响程度难以清晰地描述，各因素都具有似透明似不透明的特征.因此，为了能够更清晰地认识它、研究它，把航空货物运输系统抽象为没有物理原型、因素空间难以穷尽、行为轨迹无法控制、信息不完全的灰色系统，据此可以进行灰色模型GM（1，1）预测的研究.同时航空货运量又具有显著的无后效性（即一年的货运量对下一年度没有直接影响），而这正符合马尔可夫链预测方法的基本前提.本文结合灰色模型和马尔可夫链理论的优点，用灰色预测来揭示航空货运量时序变化的总体趋势，用马尔可夫预测来确定状态间的转移规律，得到航空货运量更精确的预测结论.

1 航空货运量灰色GM（1，1）预测模型

灰色系统理论，经过20多年的发展，已形成了以系统分析、信息处理、建模预测、决策控制为主要内容的理论体系，广泛应用于工程控制、经济管理、社会系统等众多领域［3－5］.由于中国航空货运市场的复杂多变，许多影响因素都是灰色的，因而采用灰色系统理论将更加符合航空货运市场的客观状况.此外灰色系统预测模型具有所需信息较少，计算简便，精度较高等特点，不必罗列影响其考察对象的因素数据，而是从自身时间数据序列中寻找有用信息，探究其内在规律，建立模型进行预测，因此灰色GM（1，1）模型是预测航空货运量的理想模型.航空货运量的灰色系统预测模型建立的基本步骤如下.

1.1 数据处理

将各历史年度的航空货运量构成原始序列数据x（0）

然后对各年度的原始数据逐年累加，生成一组新的时间序列数据x（1）

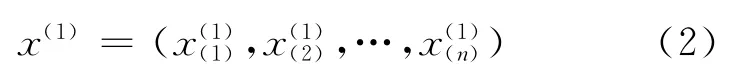
1.2 用微分方程拟合数据序列u（1），并计算出预测的累加值

建立一阶单变量的微分方程预测模型SCGM（1，1）C，其微分方程的形式为

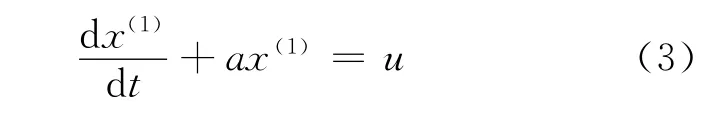
式中：a，u为待识别的灰色参数.式（1）表示一个单变量x对时间t的一阶微分方程是连续的.其离散形式为

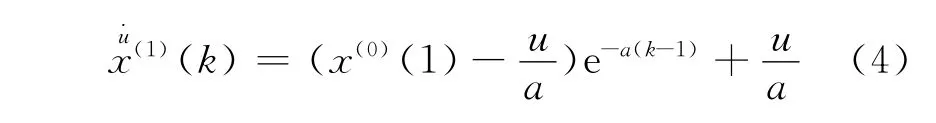
式中：

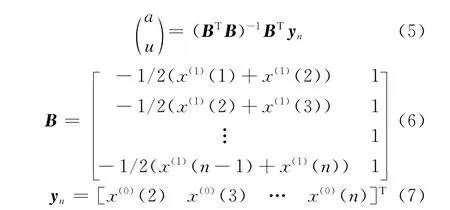
1.3 预测值的还原

要得到真正的预测结果，还需要对预测累加值进行还原处理，即对（4）式得到的模型计算值进行如下的累减

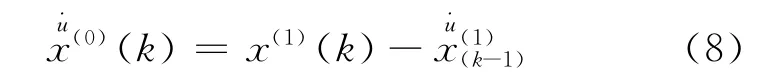
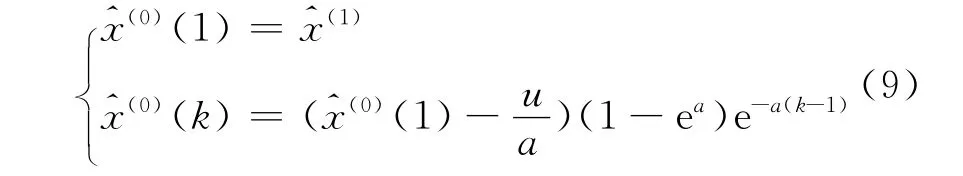
由于该模型尚未考虑各种影响因素导致的随机变化，因此用于预测还不够完善.

2 马尔可夫状态转移概率的确定

航空货运量灰色GM（1，1）预测的实质是以指数型曲线去拟合原始数据，其预测结果几何图形是一条较为平滑的曲线，因而对波动性较大的数据序列拟合较差，预测精度较低.航空系统是一个动态的时变系统，航空货运量作为灰色系统的一个行为特征量，其变化趋势呈现出了非平稳随机过程的特性，单独采用灰色GM（1，1）预测模型会使得预测结果精度较差，甚至可能增大误差.但由于马尔可夫理论具有“系统将来状态只与当前状态有关，而与过去状态无关”的性质，并且马尔可夫预测是根据系统状态之间的转移概率来预测系统未来发展，转移概率反映了各种随机因素的影响程度，反映了各状态之间的内在规律性［6－8］.因此，可以采用马尔可夫理论和方法去解决数据随机波动性较大的问题，提高预测精度.

2.1 状态划分

航空货运量的年度变化过程是一个随机的呈上升或下降趋势的非平稳随机过程，不同年度状态的边界和内涵应是变化的，为此应考虑一个具有适应性的状态划分准则，这个准则应与航空货运量的基本时序变化趋势一致.因此，对于航空货运量变化符合马尔可夫链特点的非平稳随机序列Y（k），将其状态划分为m个状态，任一个状态表示为

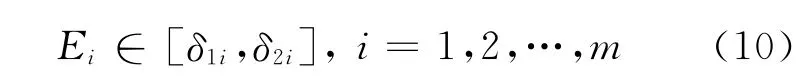
式中：Ei为第i种状态；δ1i和δ2i分别为第i种状态的上下界.由于Y（k）是时间的函数，因此灰元δ1i和δ2i也随时间变化，即状态具有动态性.

在划分状态时，要根据实际情况的不同，划分不同的区间个数.一般来说，原始数据较少时，划分区间宜少，以便增多各状态间的转移次数，从而更加客观地反映各状态间的转移规律；原始数据较多时，区间也不妨划分多一些，以便从资料中挖掘更多的信息，提高预测精度.

2.2 状态转移概率矩阵构建

由状态Ei经过k步转移到达状态Ej的原始样本数记为Mij（k），状态Ei出现的次数记为Mi，则由状态Ei经过k步转移到达状态Ej的状态转移概率为

那么，得M×M阶状态转移概率矩阵

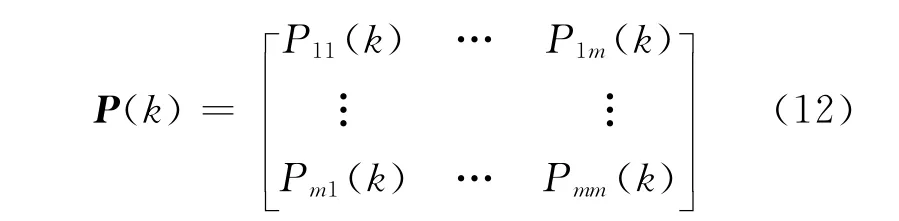
2.3 计算待预测年度的预测修正值

采用预测出的待测年份所处状态的两个边界值，运用以下公式就可以计算出待预测年度的预测修正值.

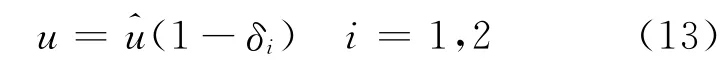
式中：δ1和δ2分别为预测出的待测年份偏差所处状态的上、下边界值.

3 实例分析

3.1 航空货运量的GM（1，1）预测

在灰色预测GM（1，1）中，所选取的原始数据为14年的数据如表1所列.

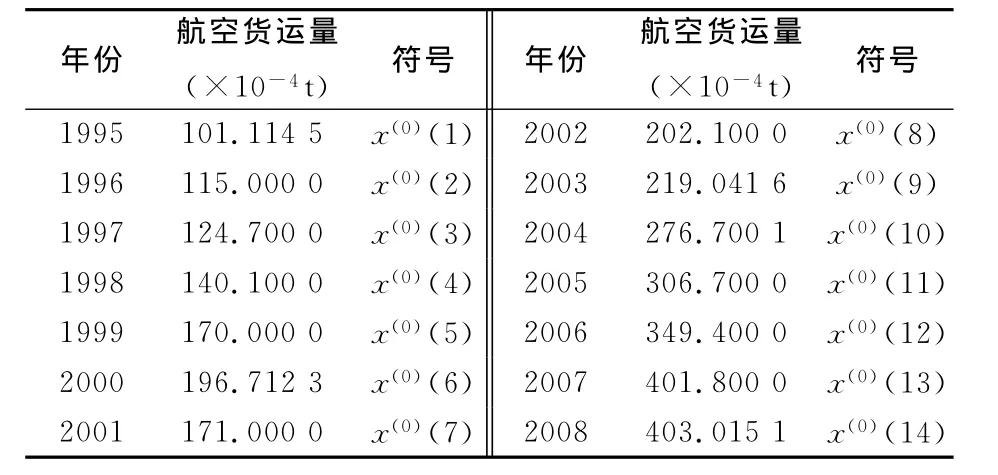
表1 1995～2008年航空货运量

根据表1数据，可以得到

可以得到我国航空货运量的灰色预测式为

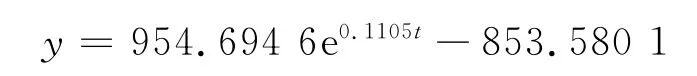
可以根据灰色预测式计算出1995～2008年度的预测值，拟合结果验证如表2所列，可以看出灰色预测模型的结果可以接受，平均误差为4.49%.下面对灰色预测模型预测GM（1，1）结果进行马尔可夫链改进.

表2 1996～2008年GM（1，1）预测结果对照

3.2 马尔可夫链转移矩阵的获得

根据马尔可夫链分析方法的应用经验和实际情况，按照年航空货运量的增幅与灰色预测结论的比较，可以划分为5种状态：（1）状态1，残差幅度小于－10%，表示预测极度低估状态.此状态在运量预测结果中没有出现；（2）状态2，残差幅度介于－10%～－3%之间，表示预测低估状态，可以理解为中国航空货运处于困难状态.在运量预测结果中出现5次；（3）状态3，残差幅度介于－3%～3%之间，表示预测合理状态.在运量预测结果中出现4次；（4）状态4，残差幅度介于3～10%之间，表示预测高估状况，可以理解为中国航空货运处于兴旺状态.在运量预测结果中出现4次；（5）状态5，残差幅度大于10%，表示预测极度高估状态.此状态在运量预测结果中没有出现.

从上面分析中可得货运量预测结果状态转移情况，如表3所列.

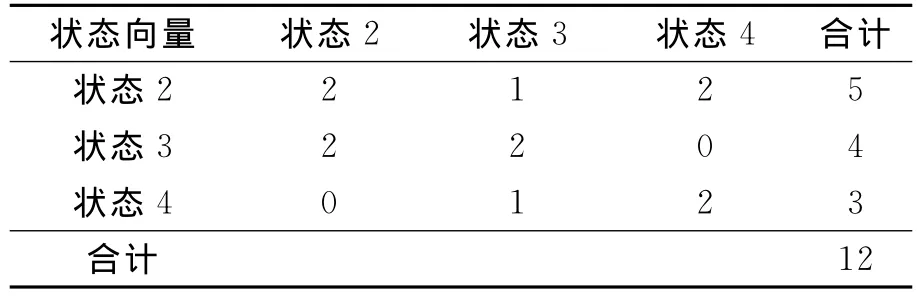
表3 航空货运量灰色预测马尔可夫状态转移

根据马尔可夫链预测原理，得到原始数据之后5年（2009～2013年）的预测状态向量如表4.

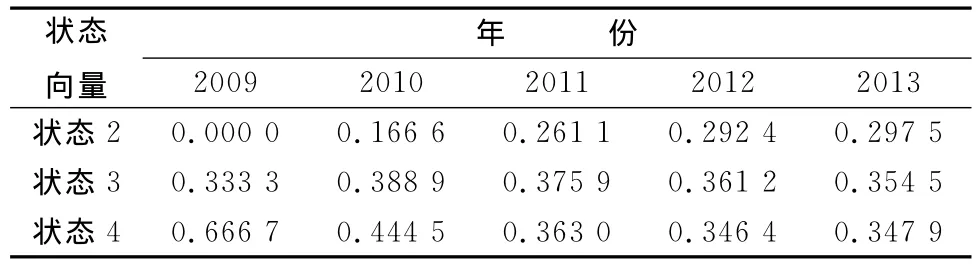
表4 航空货运量灰色预测结果马尔可夫链状态向量

3.3 GM（1，1）预测结果的马尔可夫链改进

根据以上分析，可以对GM（1，1）模型预测结果进行马尔可夫链改进结果由表5所示.

从以上灰色马尔可夫链改进方法的实证计算中可以看出，在未来的5年中我国航空货运量将逐渐上升，预测年度的状态均为高估状态，即实际发生值会高于由灰色模型预测的结果，最大的可能概 率 分 别 为 66.67%，44.45%，36.30%，34.64%，34.79%.这说明，预测年份中国航空货运市场相对于正常的动态GM发展曲线而言处于兴旺状态，即位于曲线的上方.但与此同时，这种兴旺状况的概率呈现下降趋势，而低估状态（困难状况）的可能概率由2009年的0%逐渐上升为2013年的29.75%.因此，未来5年我国航空货运市场的预测趋势是：总体以最大概率的兴旺状态呈现下降趋势，并且市场景气程度由兴旺状态逐渐向困难状态发生转变.

4 结 束 语

影响航空货运量的因素非常多，其中许多因素满足灰色系统要求，且数据多为时间序列，可以采用灰色预测模型进行运量预测，符合航空货运市场的客观状况，但是从预测结果，灰色模型受原始数据变化幅度的影响较大，预测的结果看预测的准确度并不太高.而由于原始数据具有无后效性的特点，可以通过马尔可夫链修正灰色预测模型的结果，使预测结果得到较大改善.因此确定了灰色马尔科夫链方法的研究思路，将GM（1，1）模型拟合与预测值的合理表达有机地结合在一起，不但能够得到预测年份的航空货运量，而且还可以知道货运量产生的概率情况.由GM（1，1）预测值及马尔可夫状态转移下的最大概率可知航空货运量的发展趋，说明了灰色－马尔可夫链法对航空货运量预测的科学合理性，这有助于决策者的决策行为.

［1］魏存平，刘 军.航空运输周转量的预测方法探讨［J］.民航经济与技术，2000（8）：41－43.

［2］关忠良，陈景艳，李学伟.经济数据分析预测学［M］.北京：中国铁道出版社，1998.

［3］邓聚龙.灰预测与灰决策［M］.武汉：华中科技大学出版社，2002.

［4］刘思峰，党耀国.灰色系统理论及其应用［M］.北京：科学出版社，2004.

［5］林小平，袁 捷.基于灰色模型的成都双流机场物流预测［J］.武汉理工大学学报：交通科学与工程版，2007，31（3）：457－459.

［6］张陶新.经济分析的随机动态系统方法［J］.求索，2007（3）：23－25

［7］孙荣恒.随机过程及其应用［M ］.北京：清华大学出版社，2003.

［8］耿 波，王君杰，张谢东.桥梁技术状况预测的灰色马尔可夫链模型研究［J］.武汉理工大学学报：交通科学与工程版，2007，31（1）：107－110.