动态规划的集装箱多式联运系统运输方式组合优化*
韩 骏 徐 奇 靳志宏
(大连海事大学交通运输管理学院1) 大连 116026) (中国海运(香港)控股有限公司2) 香港 999077)
针对集装箱多式联运方面的研究,Jansen,et al[1]提出了一个基于港口的集装箱运作计划的模拟研究;Bérubé,et al[2]提出运用 Dijkstra算法的原理对确定型运输时间的多式联运网络求解总成本最小的路径优化问题;苏印与李铁柱[3]、谢芳等[4]运用层次分析法对运输线路进行评价;贺竹磬等[5]采用遗传算法来解决联运路径的选择问题;靳志宏等[6]分别针对多式联运装卸与运输一体化问题、集装箱码头集卡调度优化问题、集装箱多式联运系统拼箱集运优化问题等进行了研究.本文从集装箱多式联运组织者(多式联运经营人)的角度,构筑了多式联运运输方式组合优化的数学模型,实证研究显示了该模型与方法的可行性与有效性.可为多式联运经营人在实际操作中进行运输方式组合的选择提供决策参考.
1 基于动态规划的运输方式组合优化模型
1.1 建模条件
1.2 参数说明
N为所有节点城市的个数;Mi为在第i个城市可选用的运输方式集合(“1”表示公路运输,“2”表示铁路运输,“3”表示水路运输).
Q为集装箱多式联运中货物运输总量;
飞灰主要是由燃煤中不可燃烧的灰份和部分未燃尽的碳粒组成,飞灰颗粒度越细则说明返料器分离效率越高,烧失量也就越低。经过提效改造后,通过建立0.045mm筛分监控设施,测量筛余占比由原26%,下降至12%,烧失量由原13%,下降至8%。


1.3 优化模型
目标函数)

约束条件

目标函数式(1)表示要求多式联运的总运输成本最小,其中第一部分表示将一批货物从出发地送至目的地的总成本,第二部分表示不同运输方式之间的转换引起的对货物进行换装所发生的成本.约束条件式(2)表示货物从城市i到城市i+1只能选择一种运输工具;式(3)表示货物在城市i只发生一次换装.
约束条件式(4)是确保运输的连续性.在i城市货物由第k种运输方式转换到第l种运输方式,即从i-1到i选择l,从i到i+1选择k,如图1所示.

图1 确保运输连续性示意图
约束条件式(5)、(6)表示货物在运输过程中所花费的时间必须在承运人要求的时间范围[tmin,tmax]之内,其中不等式左边第一部分均表示为货物的运输时间,第二部分为运输方式转换所产生的中转时间;式(7)、(8)表示决策变量为0-1变量.
2 MATLAB的算法与程序设计
2.1 算法设计
步骤1 将多式联运通道中的节点城市划分阶段,令每两个城市之间的运输过程为动态规划中的一个阶段,即n+1个城市有n个阶段.
步骤2 选择货物到达城市的运输方式为该阶段的状态变量,如:第2阶段的到达方式有公路、铁路,则状态变量S2可取值的范围即为1、2,第二阶段的可达状态集合S2={1,2},同理可确定其他阶段的状态变量.设计一个3×n的状态矩阵,矩阵的第k列表示第k个阶段的状态变量构造的列向量(该列向量中的第i行元素的值应为i,如Sk中不含i,则用MATLAB中特有的常量NaN填充),将所得到的3×n状态矩阵作为动态规划程序的一个输入变量.如一个3阶段的问题,各阶段的可达状态集合分别为{1},{1,3},{1,2,3},则该问题需输入的状态变量矩阵为
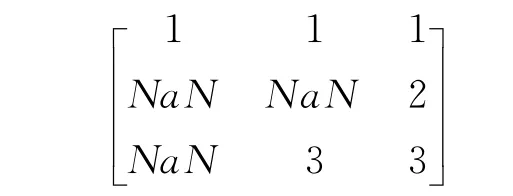
步骤3 确定决策变量和状态转移方程.在此例中,令从每一城市出发时所选择的运输方式作为该阶段的决策变量uk.状态转移方程Sk+1=uk,即第k+1阶段的状态直接等于第k阶段的决策值.
步骤4 删除不满足时间强约束的可选择方案,这也是与在一般情况下运用动态规划求解问题的区别所在.由于在模型中限定了多式联运总时间必须在顾客要求的范围[tmin,tmax]之内,因此在进行选择最优方案之前应该先排除不满足时间要求的方案.
步骤5 由边界条件k=n开始,求出在该阶段状态为sk时所有允许决策下的指标函数值,选取其中的最优值作为该阶段状态为sk时的最优值,求出最优决策(sk)并进行替换存储.以此方法向k=n-1,n-2,…,1逐步逆推,直到最后求出f1(s1),得到问题的指标函数最优值.
步骤6 由k=1开始,按照与前一步骤相反的顺序推算,记录推算结果,则可得到每阶段及全局的最优路径及最优解,存储结果并输出.
2.2 程序设计
按照上述算法设计的思路所设计的解法程序主要由以下子程序组成:(1)主函数function[p_opt,fval,tw]=dyn(x,tm,tn,SubObjFun,TransFun,ObjFun),输入状态变量矩阵和顾客要求的时间约束,输出的变量为全局最优策略组(p_opt)、最优指标函数值(fval)、完成该运输任务所需要的时间(tw);(2)阶段指标计算子函数function tmp00=SubObjFun(ii,x,u),输入阶段数(ii)、状态(x)、决策值(u),输出的变量为处于该阶段时,某一状态和决策条件下所需的一阶段成本tmp00,供主函数运行时调用;(3)状态转移计算子函数function tmp40=TransFun(ii,x,u),输入阶段数(ii)、状态(x)、决策值(u),返回处于该阶段某一状态和决策条件时下一阶段将处的状态值tmp40;(4)第k阶段至最后阶段指标函数子函数function tmp80=ObjFun(tmp00,f_opt),输入阶段指标值(tmp00)和后一阶段至最后阶段指标值(f_opt),输出值为该阶段至最后阶段指标值.
3 实证研究
将上述模型与算法应用于上海-成都间多式联运运输方式组合的选择中进行实证研究[7-8].依现状,上海-成都间多式联运通道的主要节点城市为南京与郑州.现有一个货主需要将2个TEU的集装箱从成都运往上海,运输路线为成都-郑州-南京-上海,要求在货物起运后25~30h之内到达目的地.具体数据见表1、表2及表3.

表1 集装箱多式联运各种运输方式中转距离表(成都-上海)

表2 集装箱多式联运各种运输方式的运载工具速度表

表3 集装箱多式联运各种运输方式中转时间表
对表1与2处理即可得出城市之间各种运输方式的运输时间,表3数据即为不同运输方式之间的中转时间.
集装箱运输成本根据所选择的运输工具的不同而不同,公路运输采用高速公路的运输数据,水路运输采用集装箱运输专用船,铁路运输采用集装箱运输列车.各种运输方式的集装箱运输成本计算如下[10].
1)公路运输的集装箱车运输成本

2)铁路运输的集装箱运输列车运输成本
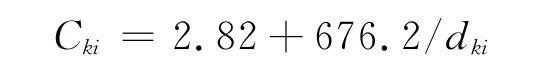
3)水路运输的集装箱船运输成本 港口i和j之间的总运输成本Cij,t的构成如下.

式中:Cij,f为港口i和j之间的燃料费用;dyij为港口i和j之间的航运天数;pf(i)为港口i的港使费;Cij,o,Cij,c,Cij,m分别为港口i和j 之间船舶的运行费用、资本费用和管理费用为t型号集装箱船的设计装载量;为构成港口i和j之间的使用t型号集装箱船的实载率;为船舶的航行速度;vrij为构成港口i和j之间的可变费用.

则可得出单位距离单箱运输成本为

式中:α1的取值如表4所列;α2主要为装卸、空箱以及准备、维修和保险费用,与船型无关,一般α2=591美元;α3为港口收费,根据港口以及船型的不同,收费标准也不同,本例中所采用的集装箱运输船运载量为3 000TEU,港口收费为84 033美元.
通过上述关于集装箱运输成本的计算,计算出此例中各城市之间的运输成本,如表5所列.
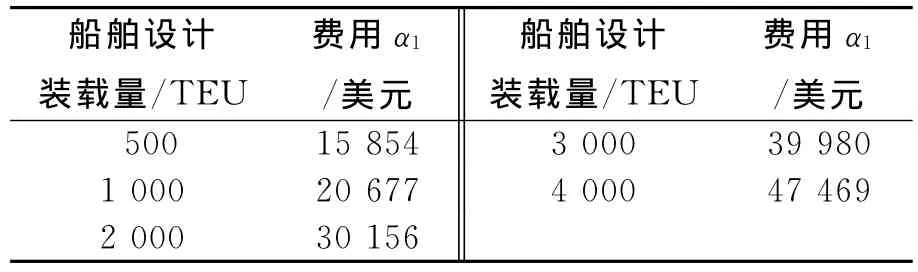
表4 各船型α1的取值
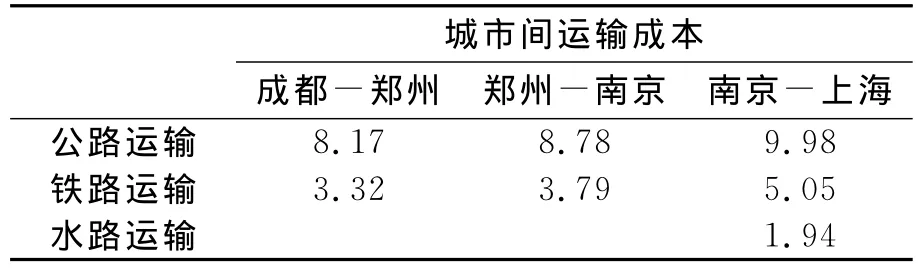
表5 集装箱多式联运各种运输方式的成本情况表美元/(km·TEU)
将上述参数输入到优化算法程序中,得到最优的运输方式组合策略为:成都-(公路)-郑州-(公路)-南京-(铁路)-上海.此时的最小运输成本为39 631美元,完成运输任务所需要的时间为29.11h.
如果对运输时间的要求放宽至起运后40~50h之内到达即可,此时再次对该问题求解,得到的最优策略组合变为:成都-(铁路)-郑州-(铁路)-南京-(水路)-上海.此时的最小运输成本为15 826美元,完成运输任务所需要的时间为46.96h.
4 结 束 语
本文对集装箱多式联运系统中各个阶段的多种运输方式的组合优化问题建立了以总运输费用最小为目标函数的优化模型,并基于现实问题对其设定了时间约束,采用动态规划的基本思想对其求解.通过MATLAB上机编程实现对该问题的求解,提供了通用的计算程序,获取了最优的运输方式组合策略.并通过成都-上海间多式联运各路段的运输方式组合优化的实证研究,显示了该模型与方法的可行性与有效性.今后的研究将致力于进一步完善模型的现实约束,并尝试采用模拟仿真技术使多式联运各种运输方式的组合优化决策问题可视化.
[1]Swinkels J,Fleuren T.Operational planning of a large-scale multi-modal transportation system[J].European Journal of Operational Research,2004,156(1):41-53.
[2]BérubéJ,Potvin J,Vaucher J.Time-dependent shortest paths through fixed sequence of nodes:application to a travel planning problem[J].Computers and Operations Research,2006,33:1838-1856.
[3]苏 印,李铁柱.国际多式联运线路选择的方法研究[J].交通运输系统工程与信息,2006,6(2):91-94.
[4]谢 芳,张 楠,纪寿文.基于AHP的多式联运路径选择[J].物流科技,2006,29(31):13-17.
[5]贺竹磬,孙林岩,李晓宏.时效性物流联运方式选择模型及其算法[J].管理科学,2007,20(1):8-12.
[6]靳志宏,朴惠淑,杨华龙.集装箱多式联运系统装卸与运输一体化优化问题[J].系统工程,2005,23(11):1-7.
[7]曾庆成,杨忠振,靳志宏.集装箱码头集卡调度优化模型与算法[J].系统工程,2006,24(增刊):187-190.
[8]郭子坚,王 诺,霍 红.多种运输模式下国内沿海集装箱港口布局模型研究[J].大连理工大学学报,2001,41(5):598-601.

