基于经验模态分解与支持向量机的旋转机械碰摩故障识别方法研究
卢艳军,刘 颖,国凤娟
LU Yan-jun, LIU Ying, GUO Feng-juan
(沈阳航空航天大学 自动化学院,沈阳 110136)
基于经验模态分解与支持向量机的旋转机械碰摩故障识别方法研究
Study on rub and impact fault of rotating machinery identifi cation method based on emd and svm
卢艳军,刘 颖,国凤娟
LU Yan-jun, LIU Ying, GUO Feng-juan
(沈阳航空航天大学 自动化学院,沈阳 110136)
碰摩故障是旋转机械常见的故障。本文以双盘悬臂转子-轴承系统的碰摩故障为例,提出基于经验模态分解和支持向量机的碰摩故障识别方法。首先对信号进行经验模态分解,得到多个固有模态函数之和,然后对每一个固有模态函数分量进行奇异值分解,得到矩阵的奇异值,将其作为信号的状态特征向量,利用支持向量机方法对多种碰摩故障进行分类,同时进行故障识别。试验结果表明,该方法的识别率明显优于传统的BP神经网络和RBF神经网络分类器,且鲁棒性好。
EMD;IMF 奇异值;支持向量机;故障识别
0 引言
碰摩是旋转机械中较为常见的一种故障。故障往往在瞬间发生,会迅速导致机器设备的严重损坏[1]。当碰摩量相对轻微时,采用较好的诊断方法及时、准确地诊断出该类故障,会对机器设备的安全、可靠运行提供有力的保证。近年来关于碰摩故障的识别与诊断取得了很多成果。例如基于负载的碰摩故障的识别方法[2]、利用小波变换对转静件早期碰摩故障进行诊断方法[3]、采用随机共振原理来检测微弱的特征信号的新方法[4]、基于LVQ(学习向量量化)神经网络的混沌时间序列分类识别碰摩故障的方法[5]、基于小波包与支持向量机的碰摩故障识别方法[6]等等。
本文应用基于EMD的特征值提取和支持向量机的诊断方法,对双盘悬臂转子系统的碰摩故障进行诊断模式识别。
1 基于EMD的特征值提取和支持向量机的诊断方法
1.1 EMD特征提取
Hilbert-Huang变换中的关键方法——经验模态分解EMD(empirical mode decomposition)是一种新的分析非线性、非平稳信号的方法[7,8]。EMD利用局部特征时间尺度,从原信号中提取出若干个固有模态函数IMF(intrinsic mode functions)分量和一个残余量。IMF分量突出了数据的局部特征,残余分量体现了信号中缓慢变化量,对它们进行分析,可以更准确把握原信号中的特征信息。然后将每一个IMF分量进行奇异值[9]提取,作为特征向量输入经过训练后的支持向量机,从而实现碰摩故障的模式识别。
EMD 把一个复杂的非平稳信号分解为有限个基本模式分量之和,其中任何一个基本模式分量(IMF)都满足以下条件:在整个数据段内,极值点的个数和零交叉点的个数至多不能超过一个;在任何一点,由局部极大值点形成的包络线和由局部极小值点形成的包络线的平均值为零。EMD算法包括以下几个步骤[10]:
1)找出x(t)的所有极大值点和极小值点,将其用三次样条函数分别拟合为原数据序列的上和下包络线;上下包络线的均值为平均包络线m1;将原数据序列减去m1可得到一个去掉低频的新数据序列h1,即

2)一般h1不一定是一个平稳数据序列,为此需对它重复上述过程。如h1的平均包络线为m11,则去除该包络线所代表的低频成分后的数据序列为h11,即

重复上述过程,使所得到的平均包络趋向零,这样得到第一个固有模态函数分量c1,它表示信号数据序列中最高频的成分。
3)用x(t)减去c1,得到一个去掉高频成分的新数据序列r1;对r1再进行步骤(1)中的分解得到第二个固有模态函数分量c2;如此重复直到最后一个数据序列rn变为一单调函数不可再分,此时rn代表数据序列x(t)的趋势或均值。上述过程可表示为

由上式可得

因此可以将任意信号分解成为n个IMF分量和一个剩余分量rn之和,其中分解出的n个分量ci分别包含信号从高频到低频的不同频率段成分,而剩余分量rn是原始信号的中心趋势。通常,前几个IMF分量集中了原始信号中主要的信息。
1.2 支持向量机
支持向量机[6,11,12](Support Vector Machine ——SVM) 是在统计学习理论的基础上建立起来的一种机器学习方法,是从线性可分情况下的最优分类面发展而来的。假设有N个样本xi及其所属类别yi,表示为。其中:;i=1,2, ,N; d为输入空间的维数。 对于标准的SVM,其分类间隔为2/,使分类间隔最大相当于最小。 因此,使两类分类的间隔最大的优化问题可表示为如下的二次规划问题:
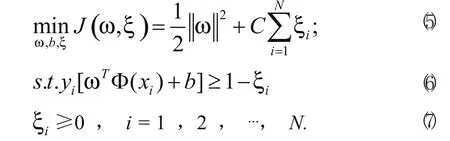
其中:ξi为松弛因子,用来保证在线性不可分情况下分类的正确性;惩罚因子C为某个指定的常数,用来控制对错分样本的惩罚程度,实现在错分样本的比例与算法复杂程度之间的折衷;Φ为非线性变换函数,可通过Φ将非线性问题转化为某个高维空间中的线性问题。在变换空间求最优分类面,设有非线性映射Φ:Rd→H将输入空间的样本映射到高维的特征空间H中。 当在特征空间H 中构造最优超平面时,训练算法仅使用空间中的内积,即Φ(xi).(xj),而没有单独的Φ(xi)出现。 因此,如果能够找到一个函数K使得K(xi,xj)=Φ(xi).(xj),则高维空间的内积运算就可以用原空间中的函数实现,甚至可不必知道变换Φ的形式。统计学习理论指出,根据Hilbert-Schmidt原理,只要一个函数K(xi,xj)满足Mercer条件,那么它就对应某一变换空间中的内积。SVM算法就是通过求解上述二次规划问题来实现对样本的正确分类。本文采用常用的核函数RBF(Radial Basis Function) ,其表达式为

支持向量机不能直接应用于多类问题分类,对于多类模式识别问题,SVM可通过两类问题的组合来实现。通常有两种方法:“一对多”策略、“一对一”策略和DAGSVM策略。针对上述算法存在无法识别具体故障的缺点,本文采用改进的算法构建多类故障分类器进行模式分类。该多分类方法描述如下:对于K类样本的训练,训练K-1个支持向量机,对于第一个支持向量机子分类器,以第一类样本为正样本,将第2, 3,…,K类样本作为负的训练样本训练SVM1,然后去掉第一类样本,在剩余的样本中,以第二类样本为正样本,将第3,…,K类样本作为负的训练样本训练SVM2,以此类推直到第K-1个分类器设计完毕。测试时,将样本首先输入第一个分类器,如果输出为“1”则判定样本类别为分类器所对应的类别,测试结束。如果不是,则进入下一个分类器,直到判断出测试样本所属的类别。
2 应用实例
本文提出对双盘悬臂转子系统信号进行EMD分解,并尝试从每个IMF中提取矩阵的奇异值作为信号的特征,构建特征矢量;然后利用支持向量机(SVM)进行模式的分类,从而对研究的系统进行碰摩故障的模式分类。
2.1 碰摩试验
双盘悬臂转子系统试验台如图1所示。1为一直流调速电机,额定转速20000r/min。2是柔性联轴节,3是左端轴承座,4是转轴,5和7是电涡流传感器(本试验共有4个测点,分别测位于中间盘左侧靠近轴承座处轴的振动位移和位于悬臂端轴承座外侧轴的振动位移),6和9是转子圆盘,圆盘6直径80mm,宽20mm,圆盘9直径80mm,宽15mm,每个圆盘上面都开有24个平衡螺栓,增加和减少平衡螺栓的个数可以调整转子的偏心量,8是右端轴承座[12]。
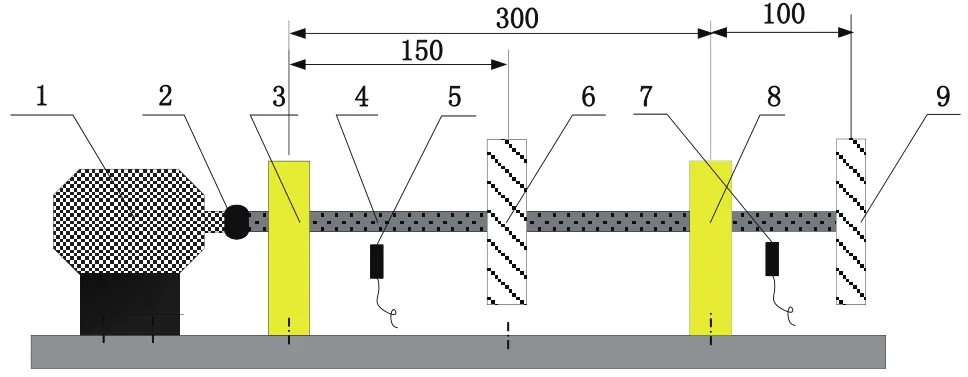
图1 双盘悬臂转子系统试验台
试验台在给定摩擦系数、间隙圆半径等系统参数后,当转子与静子的转速比ω=0.2295时系统发生碰摩。在0.2295<ω<0.688的范围内,系统发生稳定的碰摩,且随着ω的增大,碰摩程度变化总的趋势为较轻的局部碰摩、较重的局部碰摩、整圈碰摩。在ω>0.688的一定范围内,转子运动失稳,表现为复杂运动(混沌、拟周期等现象)的碰摩形式。本次试验分别使用直杆形碰摩装置和圆形碰摩装置两种,分别用来模拟全碰摩、单点碰摩、双点碰摩和不定碰摩。本文提取了中盘和悬挂盘的信号,每类故障30组数据样本,共120组样本。2/3的样本用来对支持向量机分类器设计和训练,剩下的用于检验模式识别的效果,保证SVM检测的时间为80秒左右。
2.2 试验验证

图2 IMF固有模态函数图
步骤:
1)对试验中采集的四类信号作EMD分解,图2为全碰摩故障信号的EMD分解IMF图。
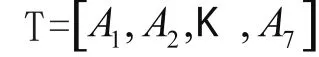

表1 EMD提取的最大奇异值
应用上述策略构建的多类故障分类器对四类模式进行识别和分类,即构建SVM1,SVM2,SVM3,分别针对全碰摩、单点碰摩,双点碰摩。
3)利用试验平台对同类信号的多组数据进行重复运行40次,取平均值作为该参数下SVM分类的正确率。尽管在特征值相同核函数不同的条件下,核函数对分类器的分类能力具有影响,但支持向量机的性能对结构(核函数) 的依赖性很小,便于在工程中应用, 特征量的选取对故障诊断准确率影响很大。
为了证明本文提出的方法的有效性,利用同样的数据信号,通过使用BP神经网络和RBF神经网络来检验识别效果,试验证明SVM方法的优越性,如表2所示。

表2 不同分类器对EMD提取特征向量的识别结果
3 结束语
研究结果表明:利用EMD提取的特征向量能够很好的服务于支持向量机的学习和测试,支持向量机可以获得很高的故障识别准确率。本文使用RBF核函数的支持向量机对双盘悬臂转子系统的碰摩故障数据进行诊断试验,试验结果显示,支持向量机在各种情况下均获得了很高的故障识别准确率,对悬臂系统的碰摩故障进行模式识别,达到故障识别的作用。
[1] 陈宏.带故障悬臂转子系统若干非线性动力学问题的研究[D].东北大学,2004.
[2] Huang Baohua,Yang Jiangang,Gao Wei.Estimation of the force s on rubbing rotor-bearing system [J].Journal of Southeast University( English Edition),1998,14(2):49-53.
[3] 刘金献,李其汉.小波变换在转子系统动静件早期碰摩故障诊断中的应用[J].航空学报,1999,20(3):220-223.
[4] 胡茑庆,陈敏,温熙森.随机共振理论在转子碰摩故障早期检测中的应用[J].机械工程学报,2001,37(9):88-91.
[5] 任辉,裴承鸣.基于LVQ神经网络的混沌时间序列分类识别[J].机械科学与技术,2001,20(6):916-918.
[6] 孟凡龙,卢艳军等.基于小波包与支持向量机的碰摩故障识别方法研究[J].测控技术,2009,28(5):71-74.
[7] Huang,N.E.,2003:Empirical mode decomposition for analyzing acoustic signal.US Patent 10-073857,pending.
[8] Huang,N. E.,M.C.Wu,S.R.Long,S.S.P.Shen,W.Qu,P.Gloersen,and K.L.Fan,2003:A confidence limit for empirical mode decomposition and Hilbert spectral analysis.Proc.R.Soc.London,Ser.A,459,2317-2345.
[9] 崔建国,李一波等.基于小波包与支持向量机的复杂信号模式识别[J].数据采集与处理2008,23(2):163-167.
[10]程军圣,于德介,杨宇.基于EMD和SVM的滚动轴承故障诊断方法[J].航空动力学报Journal of Aerospace Power,2006,21(3):575-580.
[11]C Burges.Atutorialon support vector machines for pattern recognition [J].Data Miningand Knowledge Discovery,1998,2(2):121-167.
[12]杨奎河,等.基于最小二乘支持向量机的汽轮机故障诊断[J].控制与决策,2007,22 (7):778-783.
TP18
A
1009-0134(2010)12(上)-0006-04
10.3969/j.issn.1009-0134.2010.12(上).02
2010-06-20
国家自然科学基金资助项目(50275024);沈阳航空航天大学博士启动资助项目(06YB02)
卢艳军(1968 -),女,副教授,博士,研究方向为复杂设备的故障诊断技术。

