昼间自由行驶状态下驾驶员空间距离判识规律*

赵炜华 刘浩学 冯中祥 施卢丹 蒋伟峰

(长安大学汽车学院 西安 710064)

驾驶员驾驶车辆行驶过程中,90%以上信息靠视觉获取,可见视觉信息在驾驶行为决策及相关操作中具有重要作用[1-2].人眼的视觉特征表明,对近距离的判断较为准确,而随着与目标物空间深度的加大,距离判识的准确性变差.因为“当人眼与目标物之间距离超过100 m时,空间落在双眼之间映像的差异非常小”[3-4].文献[5-6]研究了昼间动态环境中空间距离判识规律,但仅限于在不同深度距离下,判识距离随速度的变化趋势,缺乏深度距离对距离判识的影响分析.本文通过实际道路试验,以探究人在动态环境中对障碍物空间距离判识的规律,分析深度距离和速度对判识的影响,并建立定量变化的数学模型.

1 实验设计与被试选择

1.1 实验设计

研究遵照心理学实验设计与方法,最大限度控制了影响因素,试验现场设计如图1所示.

1)试验道路为1 100 m直线区段,方向为东西走向,道路两端等条件设置实验车辆具有足够的加速和匀速区段;实验时间区段为14:00～18:00时,天气晴到多云,所有被试试验过程中基本控制在等照度环境(15 000 lx～40 000 lx).

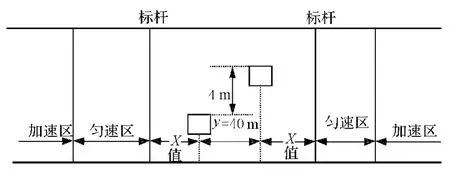
图1 实验现场设计

2)车辆行驶深度方向第一辨识点障碍物,按近、中、远分别设为25,75,125 m设置,2个障碍物之间的相对距离为40 m.车辆试验速度均按0,20,40,60,80和100 km/h的6级速度进行控制.

3)被试驾驶员在不同设计速度下,行驶至判识基准线时,直接报出绝对空间距离X和相对距离Y的主观判识距离数值.考虑到光线照射方向和环境差异的影响,两个方向均进行一次试验,取两次判识平均值为驾驶员在不同速度和深度距离下的判识结果.

4)实验车辆为福特全顺JX6541B-H型,车速表进行了标准校验,并采用ISKRA-1D型非接触式车速测试仪进行间断监控,以保障试验车速误差有限;道路障碍物颜色选用暖色系的红色及冷色系的绿色,其尺寸为0.5 m×0.5 m×1.3 m;环境照度用LX1330B型数字照度计测试,用以监测整个实验开始到结束的照度变化.

1.2 被试选择

被试驾驶员按照随机性原则选取,并注意相关因素的影响,共选取不同行业,驾驶经历、职业、年龄和驾龄的32名男性驾驶员.要求驾驶年限均超过5年驾龄,持有B照以上驾驶执照资格.技术均娴熟,且有良好的驾驶习惯,视觉机能正常,无生理缺陷和重、特大事故经历.被试基本情况如表1所列.

表1 被试驾驶员基本情况分类表

2 实验结果

2.1 距离判识数据

按照试验方案设计,在不同深度距离和速度下,被试驾驶员分别进行距离判识.统计分析判识结果,全部判识结果符合或接近正态分布,取全部被试距离判识数据平均值,作为不同速度和距离条件下距离判识结果.红色障碍物距离判识结果,如图2所示.

图2 红色障碍物距离判识结果

根据相同数据处理方法,获得绿色障碍物距离判识结果如图3所示.

2.2 被试判识回顾

试验结束后,驾驶员普遍反映,在不同深度距离下,绝对距离X的判识值随着车速不断提高而逐渐下降,相对距离Y判识值也不断下降,但下降程度不如绝对距离明显;随着深度距离增加,判识绝对距离下降明显程度降低,而相对距离判识受深度距离变化影响较小,随速度判识值变化明显.不同颜色障碍物的距离判识差异明显,绿色障碍物距离远于红色,且随着深度距离增加,差异愈加明显.

图3 绿色障碍物距离判识结果

3 判识距离变化规律

3.1 不同颜色判识差异分析

被试回顾结果显示,不同颜色障碍物判识距离差异明显.判识记录数据也表明,绿色障碍物判识距离大于红色.在实验过程中,由于被测试者在相同条件下参加红、绿两色障碍物距离判识,故在此选用Paired-T检验方法进行差异检验.在不同速度和深度距离下,不同颜色障碍物判识距离检验结果如表2所列.

表2 昼间不同颜色障碍物判识配对T检验结果

由表2可知,在不同距离和速度时,对于红、绿两色障碍物判识,绝对距离和相对距离检验显著程度Sig值,仅有个别小于0.05,即红、绿两色障碍物距离判识仅在个别距离和速度时,差异显著.反之,结果表明,在试验统计数据中,不同颜色障碍物距离判识数据无统计学差异.

3.2 判识距离变化规律

由于不同颜色障碍物判识距离,统计学意义上差异不显著,将红、绿2色障碍物在不同深度距离和速度下的判识距离取平均值,不仅可以获得自由行驶状态下距离判识变化规律,而且可以提高数据准确性.经上述数据处理后,获得距离判识数据变化如图4所示.

图4 障碍物距离判识结果

由图4所示可见,绝对距离判识随着速度和深度距离的变化,在空间中形成一个一曲面.通过曲面回归分析,逼近判识距离随速度和距离变化的函数.考虑到指数函数变化趋势,在此选用二元三次函数进行逼近,函数见式(1).

式中:z为驾驶员判识距离;x为第一判识点深度距离;y为车辆运行速度;ε为随机误差.

被测试者在不同深度距离和速度下,进行了多次距离判识,将判识结果代入式(1)中,获得如式(2)所示线性方程组.

式中:k为距离判识点数,k=1,2,…18;i为深度距离设置数,i=1,2,3;j为试验设计速度数,j=1,2,…,6.

选用最小二乘法解方程组,求得方程组系数解.将计算获得的系数解代入式(1)中,得曲面回归函数见式(3).

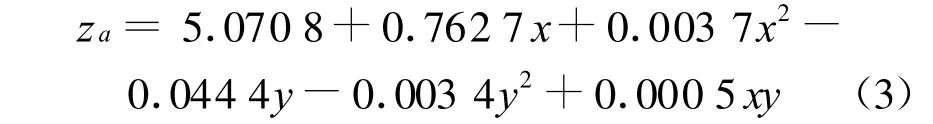
式中:za为驾驶员判识绝对距离;x为第一判识点深度距离;y为车辆运行速度.

采用同样处理方法,获得相对距离判识变化函数见式(4).

式中:zr为驾驶员判识绝对距离;x为第一判识点深度距离;y为车辆运行速度.

在试验方案中设计速度和距离下,由逼近函数求得的判识距离与实测数据误差在有限范围内.将相关数据代入SPSS进行分析,经统计检验知,模型判定系数R2为1,进入计算变量为X2,Y2,XY,X,Y.经方差分析表明,总体显著性概率值sig为0,小于0.001,拒绝总体回归系数为0的原假设.可见计算模型有效,拟合效果非常好.

经计算及分析判识距离实际得出,当深度距离大于等于45 m时,模型计算符合实际;当深度距离介于25～45 m间,车辆运行速度小于 80 km/h时,模型有效;当深度距离介于10～25 m,速度小于50 km/h时,计算模型有效.距离小于10 m时,模型计算偏差不符合人对距离判识实际.综上分析,得出距离判识随深度距离和速度变化趋势如图5所示.

图5 障碍物距离判识结果

由图5可见,在自由行使状态下,驾驶员动态空间距离判识准确性,受到速度和深度距离影响.随着深度距离增加,判识距离逐渐减小,判识准确性变差;随着深度距离增加,判识距离增加,判识准确性变差.自由行使状态下,由于速度和深度距离的交互影响,空间距离判识在空间中形成一个曲面.

4 结 论

1)自由行驶时,驾驶员对空间绝对距离判识受深度距离和行驶速度影响大.随着障碍物深度距离增加,绝对距离判识值增大,随着速度增加,绝对距离判识值减小.

2)相对距离判识受深度距离影响小,速度变化影响大.

3)二元二次函数可很好逼近空间距离判识变化,与试验测得数据差异非常小,拟合度高.

[1]周荣刚,张 侃.多参照系条件下信息获取方式对绝对方位判断的影响[J].心理学报,2008,40(11):1137-1148.

[2] 袁 伟,付 锐,郭应时,等.汽车驾驶人感知-决策-行为模式[J].长安大学学报:自然科学版,2007,27(3):80-83.

[3]刘 强,陈安涛,王 琪,等.知觉加工中存在颜色类别知觉效应的证据[J].心理学报,2008,40(1):8-13.

[4]Abdulhai B,Ritchie S G.Enhancing the universality and transferability of freeway incident detection using a Bayesian neural network[J].Transportation Research:Part C,1999,7(5):261-280.

[5]刘浩学,赵炜华.驾驶员昼间动态环境暖色调障碍物空间距离判识规律[J].交通运输工程学报,2009,9(2):105-109.

[6]赵炜华,刘浩学.色调对昼间动态环境中驾驶员空间判识的影响[J].长安大学学报:自然科学版,2009,29(4):85-90.