一种基于多模板的超宽带信道估计算法

徐 微 赵加祥 王 东 艾小溪

(南开大学信息技术科学学院 天津 300071)

1 引言

脉冲超宽带(IR-UWB)技术在短距离高速率无线通信应用中正受到广泛的关注[1−3]。对脉冲超宽带系统来说，低复杂性，低功耗，低成本的发射机是很容易实现的。但由于发射超宽带脉冲很窄(亚纳秒级)，带宽非常宽，又通过复杂的多径环境传输，IR-UWB系统中接收机的设计成为一个极大的难题和挑战。为了实现低复杂性，低功耗，低成本的接收机，文献[4]中提出了基于能量检测和自相关检测的非相关接收机结构。这种非相关接收机不需要信道估计，在很大程度上降低了硬件实现的复杂性。但由于UWB发射功率很低，非相关接收机很难收集到足够的信号能量用于解调，无法取得很好的接收性能。Rake接收机可以充分利用超宽带的多径分辨能力，收集沿不同路径在不同时刻到达的脉冲能量以提高接收的信噪比，降低误码率。然而使用Rake接收机就不可避免的需要解决一个关键问题信道参数估计。

针对IR-UWB系统中的信道估计问题，研究人员提出了许多估计算法。文献[5,6]分别给出了基于极大似然准则和的最小二乘算法(LS)的信道估计方案。虽然这两种算法都具有较高的精度，但它们在硬件实现上都需要高于千兆赫兹采样的A/D转换器，而如此高速的A/D转换器造价和功耗都很高，大大提高了接收机的成本和复杂性，不适于在要求低成本的超宽带系统中应用。文献[7]提出了一种新的UWB信道估计方法，它利用训练序列来设计一种压缩滤波器，并利用它和输入信号做卷积得到冲击响应。这种方法也具有较好的性能，但在硬件实现上需要一个匹配滤波器，一个抽样器，一个压缩滤波器，这使得接收机的复杂度非常高，而且算法也很复杂。

本文针对码片率抽头间隔的脉冲超宽带系统离散信道，提出一种基于帧级采样速率的信道估计算法，避免了高于千兆赫兹采样的A/D转换器的使用，大大降低了相关接收机的复杂度。本文算法中引入了若干个复合信道参数，每个复合信道参数都含有几个独立信道参数的线性组合。在接收端，将接收到的信号与预先设计好的多个模板分别相乘，再进行帧级的积分采样。信道估计算法分为两步。(1)利用每个模板得到的帧级采样数据，对信道进行分段估计，即得到获得所有复合信道参数的极大似然估计值。(2)联合不同模板得到的复合信道参数估计值，得到每个独立的信道参数的极大似然估计。通过仿真，验证了该方法的可行性。

2 数学模型

2.1 发送信号模型

考虑超宽带系统单用户的情况，并假定发射机和接收机已经同步。在信道估计阶段，发送端要发送的训练序列的信号可表示为

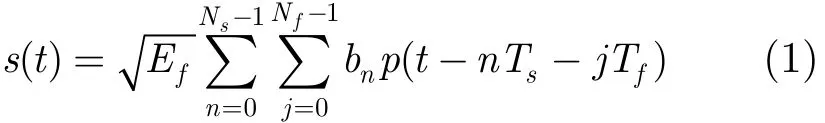
其中p(t)是发送的单个脉冲波形，脉冲宽度记为Tp，且具有归一化能量，即∫p2(t)dt=1，Ef表示每帧内的总能量，Tf为帧周期，Tc为码片周期，且Tc≥Tp。每帧内含有Nc个码片，即Tf=NcTc。Nf为一个信息符号所包含的帧数，则符号周期Ts=NfTf，bn是发送的训练序列比特，信道估计时训练序列全部为1，训练序列总长度为Ns。

2.2 信道模型

码片率抽头间隔的超宽带信道可以表示为

其中，L表示信道的长度，hl表示第l条多径的幅度增益。信道估计的目的就是获得信道参数向量h=[h0h1…hL−1]的估计值。假定没有帧间干扰，即信道的延时扩展LTc小于发射信号的帧周期Tf，利用Tf=NcTc，有L≤Nc。h中的信道长度L为未知变量，为了便于估计，引入一个新的Nc维的向量p

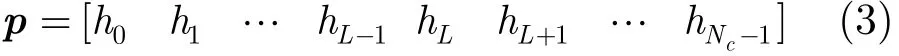
其中，hL及其之后的信道参数全部为零。则在接收端，接收到的信号可以表示为

3 UWB信道估计算法

本文提出的UWB系统的信道估计算法框图如图1所示。首先，接收到的信号与预先设计好的S个模板W1(t), W2(t),…,WS(t)分别相乘，并以周期Tm进行积分采样，其中Tf＜Tm＜2Tf。用Yi[ n]表示由第i个模板Wi(t)得到的第n个采样值，则Yi[ n]可表示为

图1 信道估计算法实现的系统框图

其中i∈{1,2,…,S }。利用这些帧级采样数据，可以获得信道参数的极大似然估计值。

3.1 模板的设计

在信道估计中使用了S个模板，模板个数S可调，它是Nc的一个因子，即Nc=SM，其中M也是Nc的一个整数因子。每个模板都是以采样间隔Tm为周期的周期函数，其中Tm=Tf+STc。第i个模板Wi(t)在一个周期[0Tm]内的时域表达式可写为

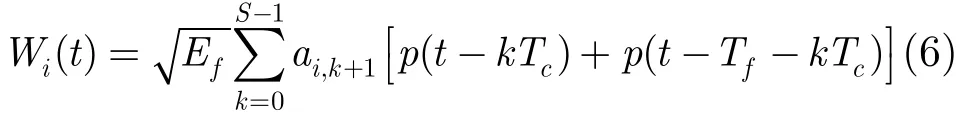
其中ai,k+1∈{1,0,−1}是第i个模板的第k+1个脉冲的幅度系数。每个模板的S个脉冲幅度系数可以有多种不同的组合。若将所有模板的脉冲幅度系数的组合记为，那么对所有的模板，ai,k+1的选取只要满足

其中rank(˙)表示矩阵的求秩运算。以S=5为例，图2给出了一套模板的时域波形示意图。

图2 S=5时，模板的时域波形示意图

3.2 信道估计算法

为了便于描述本文提出的信道估计算法，先来定义几个参量。首先，将长度为Nc(=SM)的信道参数向量p平均分为M段，每段含S个参数，即p=[h0h1… hm… hM−1]，其中S维的向量hm表示信道的第m段。

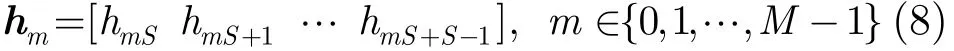
用向量ai表示式(7)中矩阵A的第i行(即第i个模板中的S个系数)，即

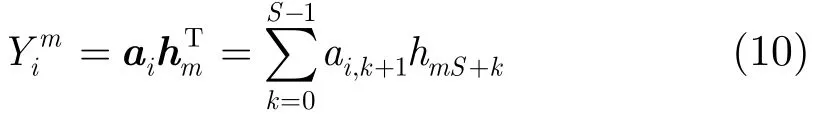
其中m∈{0,1,…,M−1}，i∈{1,2,…,S }。

接下来的信道估计算法分为两步。具体过程如下：

步骤1 利用所有模板得到的帧级采样点序列和极大似然估计准则，得到所有复合信道参数{|i=1,2,…,S; m=0,1,…,M−1} 的极大似然估计值。 以第i个模板为例，利用从该模板收集到的采样序列{Yi[ n]}，可以得到M个复合信道参数的极大似然估计值。将式(4)和式(6)代入到式(5)，可以证明采样序列{Yi[ n]}具有如下的分解形式(证明略)：

其中m∈{0,1,…,M−1}，q∈{0,1,…,Q−1}，Q= N/M (N是每个模板的总的采样点数)。 从式(11)中可以看出，采样序列{Yi[ n]}可以分为M组：{Yi[ qM]}，{Yi[1+qM]}，…，{Yi[ M−1+qM]}，每组序列中的所有采样值都包含着一个相同复合信道参数，例如，第1组序列{Yi[ qM]}中每个采样值都包含复合信道参数，第2组序列{Yi[1+qM]}中每个采样值都包含复合信道参数。

因为第m组序列{Yi[ m+qM]}中每个采样值都包含复合信道参数，利用第m组序列{Yi[ m+qM]}在式(11)中的分解式，可以得到复合信道参数的极大似然估计值为

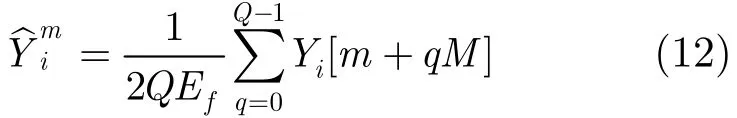
对第i个模板得到的采样序列{Yi[ n]}中的每组序列都进行上述处理，即可得第i个模板的M个复合信道参数的极大似然估计值

步骤2 联合第1步中由S个不同模板得到的所有复合信道参数，获得每个独立的信道参数hl的极大似然估计。利用的定义式(10)，可知所有模板的第m个复合信道参数，即，都含有相同的S个独立的信道参数hmShmS+1…hmS+S−1，具体展开式如下：

利用上述运算，可以得到Nc维信道参数向量p=[h0h1… hM−1]中所有S维信道参数向量h0h1…hM−1的极大似然估计值，即可得=[…]。

4 仿真结果

本节通过超宽带通信系统仿真验证本文提出的信道估计算法的可行性。在仿真中，发射的超宽带脉冲波形选用高斯波波形的2阶导数，脉冲宽度为Tp=1 ns，超宽带信道用文献[8]中描述的信道CM4来产生。其它的参数选取如下：Nc=100，Tc=1ns，Tf=100ns，Nf=25。模板数S依次选为5，10，20，用于信道估计的训练序列长度Ns选为30和100。

图3给出了模板数S=10，训练序列长度为Ns=30，发射端信噪比为8 dB时，基于多模板的信道估计算法的一次实现，其中，图3(a)表示实际的信道冲击响应，图3(b)是估计的得到信道冲击响应。

图4给出了当模板数S依次选为5，10，20时，本文提出的基于多模板的信道估计算法的误比特率性能。作为比较，还画出了文献[9]中信道估计算法的误比特率曲线和理想信道估计(即假定接收端完全知道所有信道信息)下的误比特率曲线。注意，本文提出的算法的采样速率要远远低于文献[9]中的算法，按照仿真中所采取的仿真参数计算，当模板数S依次选为5，10，20时，本文算法的采样间隔Tm(=Tf+STc)依次为105 ns，110 ns，120 ns。而文献[9]中的算法是基于码片级采样的，在此次仿真中采样间隔为1 ns。图5比较了本文算法和文献[9]算法的均方误差性能曲线。同时按文献[9]中给出的全局的克拉美罗下界(global CRLB)公式，画出了训练序列长度Ns为30时的克拉美罗下界。从图中可以看出，基于多模板的信道估计算法的误比特率和均方误差都随着训练序列长度和模板数S的增加而逐渐降低，效果也越来越接近文献[9]中的算法。当模板数S=20，训练序列长度为Ns=100时，本文的算法已优于文献[9]中的算法。

图3 信噪比为8 dB时，基于多模板(S=10)的信道估计算法的一次实现

图4 理想信道估计，文献[9]中信道估计和基于 多模板的信道估计算法的误比特率性能曲线

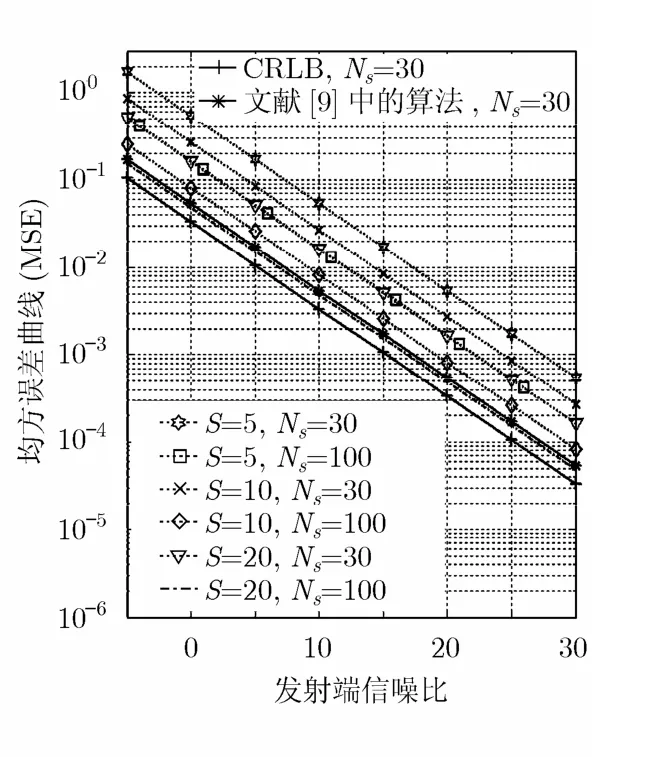
图5 文献[9]中信道估计和基于多模板的信道估计的均方误差性能曲线

5 结束语

本文提出一种基于帧级采样速率的多模板信道估计算法。该算法的主要优势是避免了高于千兆赫兹采样的A/D转换器的使用，大大降低了相关接收机的复杂度。通过仿真，验证了该方法的可行性。

[1] Abou-Rjeily C. Pulse antenna permutation and pulse antenna modulation: Two novel diversity schemes for achieving very high data-Rates with unipolar MIMO-UWB communications[J]. IEEE Journal on Selected Areas in Communications, 2009, 27(8): 1331-1340.

[2] IEEE P802.15.4a-2007. Wireless Medium Access Control(MAC) and Physical Layer (PHY) Specifications for Low-Rate Wireless PANs [S], 2007.

[3] Stoica L, Rabbachin A, Repo H, Tiuraniemi T, and Oppermann I. An ultra-wideband system architecture for tag based wireless sensor networks[J]. IEEE Transactions on Vehicle Technology, 2005, 54(5): 1632-1645.

[4] Witrisal K, Leus G, Janssen G J M, Pausini M, Troesch F,Zasowski T, and Romme J. Noncoherent ultra-wideband systems: An overview of recent research activities[J]. IEEE Signal Processing Magazine, 2009, 26(4): 48-66.

[5] Lottici V, D’Andrea A, and Mengali U. Channel estimation for ultra-wideband communications[J]. IEEE Journal on Selected Areas in Communication, 2002, 20(9): 1638-1645.

[6] Yang L and Giannakis G B. Optimal pilot waveform assisted modulation for ultra-wideband communications[J]. IEEE Transactions on Wireless Communication, 2004, 3(4):1236-1249.

[7] Alizad A R, Alipanahi B, Shiva M, Jamali S H, and Nader-Esfahani S. Channel estimation for time-hopping pulse position modulation ultra-wideband communication systems[J]. IET Communications, 2008, 2(8): 1051-1060.

[8] Foerster J. Channel modeling sub-committee report (Final).IEEE P802.15 Working Group for Wireless Personal Area Networks (WPAN), 2003.

[9] Wang X and Ge H. On the CRLB and low-complexity channel estimation for UWB communications[C]. IEEE 41st Annual Conference on Information Sciences and Systems,Baltimore, Mar. 14-16, 2007: 151-153.