一种新型的认知无线电频谱空穴自适应检测算法

王红军 毕光国

①(东南大学移动通信国家重点实验室 南京 210096)②(电子工程学院安徽省电子制约重点实验室 合肥 230037)

1 引言

随着无线通信技术的发展，频谱资源贫乏的问题将日益严重，认知无线电被认为是一种解决频谱资源匮乏的有效方法。认知无线电[1−3]被定义为一种能够实时意识到周围电磁环境的变化并不断调整系统参数且主动学习以适应其所处电磁环境的网络。认知无线电设备在开放的频段[2]内必须服从“互存”的原则[4,5]，实现认知用户(非授权用户)不对周围主用户(授权用户)和其他正在通信的用户产生干扰，实时地“借用”“频谱空穴”进行信息传输，在主用户需要使用被“借用”的频谱时实时退出，切换至下一个空闲频谱上去进行通信。认知必须贯穿整个通信过程。

认知无线电目前虽然仍受到很多条件和技术制约，处于起步阶段，但其首要任务就是认知用户首先必须有检测主用户、搜索和判定“频谱空穴”的能力，也即必须具有强背景噪声中弱信号检测的能力。认知用户对主用户进行检测的方法主要包括匹配滤波器法[6]、周期特征检测法[7,8]、多抽头频谱检测法[9]、循环谱检测法[10]、能量检测法[11−13]、LMS滤波算法[14−16]和高阶谱检测算法[17,18]。匹配滤波器法需要预先知道主用户的波形与调制样式；能量检测法只能给出信号大致的频段，对于认知无线电需要精确的频域信息而言这远远是不够的；循环谱检测法需要有连续和无限的开窗长度，这在现实中是难以满足的，另外由于多径衰落和阴影的影响，包括周期特征检测法、多抽头频谱检测法、LMS滤波算法和高阶谱检测算法在内的上述算法在低信噪比[19,20]或临界判决时难以有效实现对强噪声背景下的弱信号检测，检测概率较低。

本文结合运算复杂度低收敛性好的频域块自适应滤波技术，提出了一种新的强噪声背景下的基于三重矩阵累积估计的自适应频谱空穴检测算法。

2 自适应频谱空穴检测算法原理

自适应频谱空穴检测算法主要由频域块自适应算法和频谱空穴检测算法两个模块组成，其中频谱检测算法包含了矩阵累积运算、频域重构和频域平滑，算法基本流程如图1所示，算法简称为BFFTAA-RAPF检测算法，其中BFFTAA(Block-FFT Adaptive Algorithms)为基于频域块傅里叶变换的自适应滤波算法，RAPF为检测算法，包括矩阵重构(Reshape)、累积估计(Accumulate products estimation)和频域平滑(Frequency-domain smoothing)3个部分。

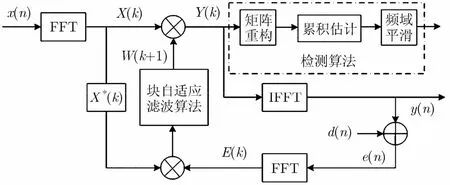
图1 BFFTAA-APRF算法流程

2.1 频域块自适应滤波算法

频域块自适应滤波算法实质是以频域来实现时域分块LMS算法，即将时域数据分组构成有N个点的数据块进行算法处理，同时在每块上滤波权系数保持不变。算法首先对采集数据进行块自适应滤波，然后在此基础上进行信号检测。其中频域块傅里叶变换自适应算法(BFFTAA)流程为

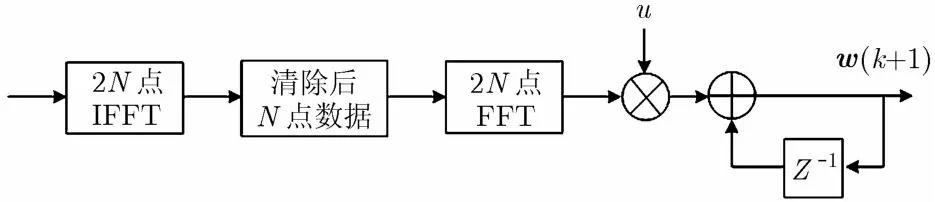
图2 频域块自适应滤波算法

算法将量化的数据分为M段，每段有N个采样点，数据块的大小即为滤波器抽头系数的个数。众所周知，第k个数据块内时域自适应滤波方程为

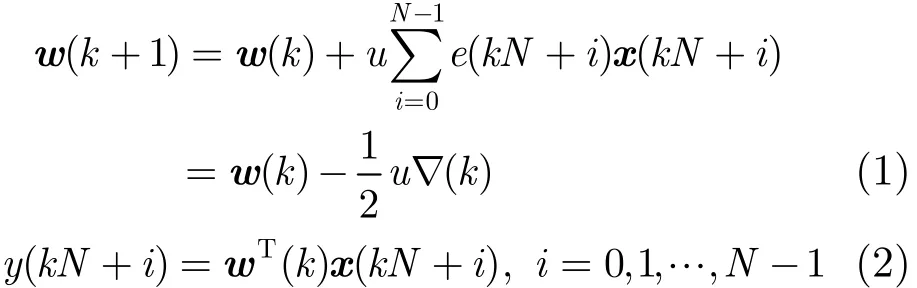
式中w(k)是第k块内滤波器时域权系数的矢量，即

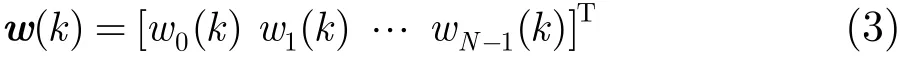
x(n)是在n时刻滤波器含有N个最新的输入信号样本，可看成是N个抽头延迟线的输出，即

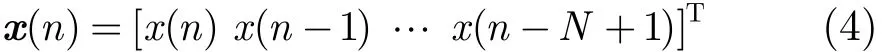
u为权系数更新步长。e(n)是误差序列，它等于期望响应与滤波器输出之差，即

频域块自适应算法在频域上采用50%重叠保留法来实现，使计算量比时域大为减少，50%的重叠计算对BFFTAA和后续的三重矩阵累积检测算法都具有最高的运算效率。算法将每段N点数据进行离散傅里叶变换，权系数每N个样点更新一次，每次更新都是由N个误差信号样点累加结果来控制。

具体过程为通过对时域权系数矢量w(k)增加N个零，再利用2N点的FFT得到频域权系数矢量：

其中W(f)为2N×1的向量，即频域抽头向量长度为时域抽头向量长度的两倍。将第(k-1)块与第k块输入数据进行2N点FFT变换，并令X(f)的元素组成对角矩阵：

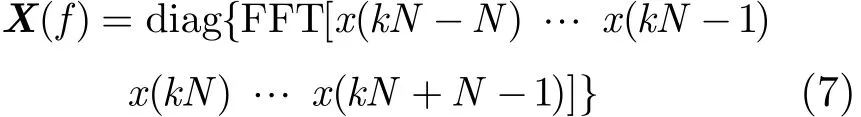
由上述推导，可以得到如下表达式：

滤波器对应的时域和频域输出则为上式的最后N项。

根据如上结果，算法由此同时进行权系数更新和频谱空穴检测两步运算。

2.2 权系数更新

误差序列的FFT变换为

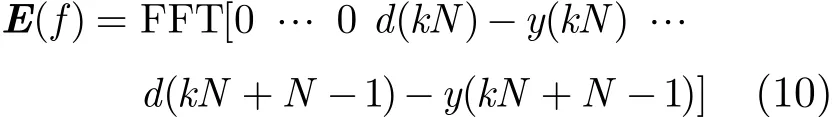
取下式的前N项即为梯度：

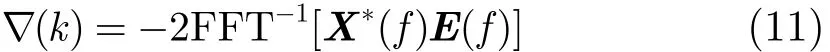
最后得到频域滤波权系数更新公式为

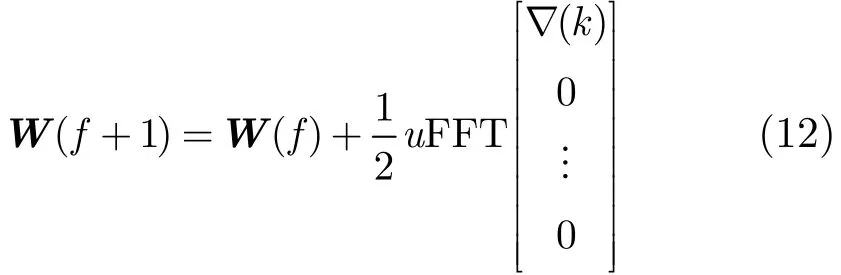
利用式(12)对式(9)进行迭代则可以得到Y(f)不断更新的输出。

2.3 频谱空穴检测算法

首先利用每段经过自适应滤波后得到的频域数据Y(f)共共轭构造一个N×N的Hankel矩阵B(f)：

然后将Y(f)与构建的Hankel矩阵B(f)进行三重计算。

在完成重构和三重累积计算后，得到累积估计值C(f)。经过不断的迭代和更新，以及对每段值C(f)进行累加和平均后得到平均累积估计值：

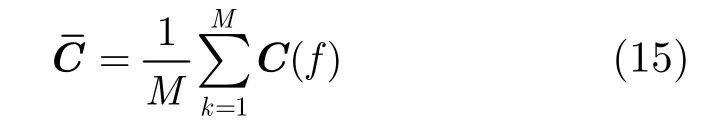
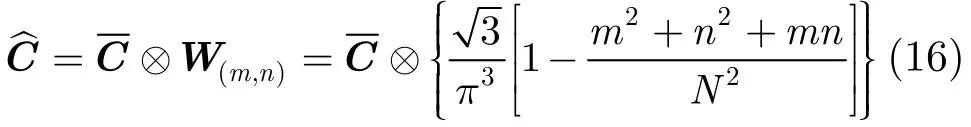
式(16)完成对估计值的平滑，式中W(m,n)为Rao-Gabr窗，N 是FFT长度，其中采集点数据系列。

在式(14)中采用了三重累积计算，进一步地抑制了噪声，提高了检测SNR。

2.4 门限确定

噪声虽然随机性强，但其谱分量通常是频段内是均匀分布的。针对授权频段之间均有频率保护间隔，因此可以在相对长的时间内，对欲检测频段的上下邻近保护频段进行噪声水平测试，对FFT后得到的数值按照式(16)进行算法处理后得到C，再计算出方差，记为σn。再对频段内的数据利用上述算法求解出的进行处理，得出σD。

取门限σT=σn，若σD≤σT，则判决处理数据为噪声；若σD＞σT， 则判决主用户(授权用户)存在。

实际应用中，门限σT应取得略大于σn，以更好地抑制噪声；同时也不能取得太大，以防过多地损失主用户的信息，仿真表明，σT的取值大于σn0.5 dB即可。尽管这种处理方法以损失部分信息为代价来抑制噪声分量，但在实际应用中有着良好的效果。

3 仿真与性能分析

无论自适应滤波还是多重累积运算，都是有效克服强背景噪声的有效手段。仿真采用蒙特卡洛仿真法，主用户信号设定为QPSK调制信号，数据长度为2048点，分为32块，每块长度为64，仿真次数为10000次。仿真噪声不失一般性，假定为高斯噪声类型。

检测算法的性能由检测的谱峰图和操作特性曲线(ROC)来描述，为比较算法的性能，在相同条件下同时对最为经典的能量检测法[13]、LMS滤波法[15]和双谱检测法[18]进行了仿真。图3-图6表述了在信噪比为-13.2 dB时检测到的信号谱峰图。从图中可以看出，BFFTAA-RAPF算法因构建矩阵时数值有取舍导致峰值略有损失，但明显可以在强噪声中检测出信号，而双谱检测虽然对白噪声有抑制作用，但在信噪比很低的情况下也难以明确给出判决结论，时域LMS滤波法和能量检测法在-13.2 dB的信噪比下基本失去检测作用。

图中的纵坐标为CSI(Comparative Signal Intensity)，横坐标为频率偏移量。从图3～图6的对比可以看出，论文提出的检测新算法的性能明显优于其它3种常规算法的性能，显然能够在极低信噪比的背景下有效地将信号从噪声中分离出来。

在图7的ROC曲线中，横坐标表示虚警概率，纵坐标表示检测概率。为了比较，本文对能量检测、时域自适应滤波检测和双谱检测的性能也进行了仿真。从图7曲线上可以看到，如果以检测概率80%作为性能标准，那么在AWGN信道中，论文给出的检测算法在信噪比为-13.2 dB时仍然具有较高的检测概率和较低的虚警概率。可见算法完全能够工作在低信噪比的检测环境里，可以逐步降低强噪声凸显弱信号，实现强噪声背景下的弱信号检测，并且比其它算法更能适应复杂多变的无线电磁环境。

4 结论

认知无线电可广泛应用于通信领域，频谱认知算法将得到越来越广泛的重视。本文结合认知无线电需求，提出了一种新型的频谱空穴检测算法，其核心是对经频域块自适应滤波后的数据进行累积计算得到频域估计值，经过判决后获得检测结果，该BFFTAA-RAPF检测算法明显可应用于认知无线电领域。

图3 能量检测谱峰图

图4 时域LMS检测谱峰图

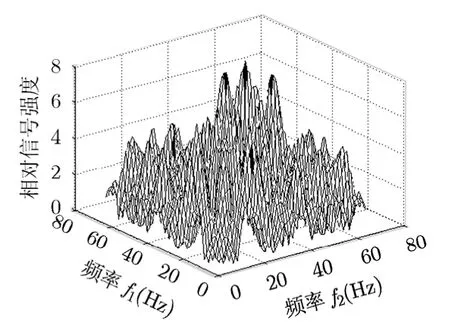
图5 双谱检测谱峰图

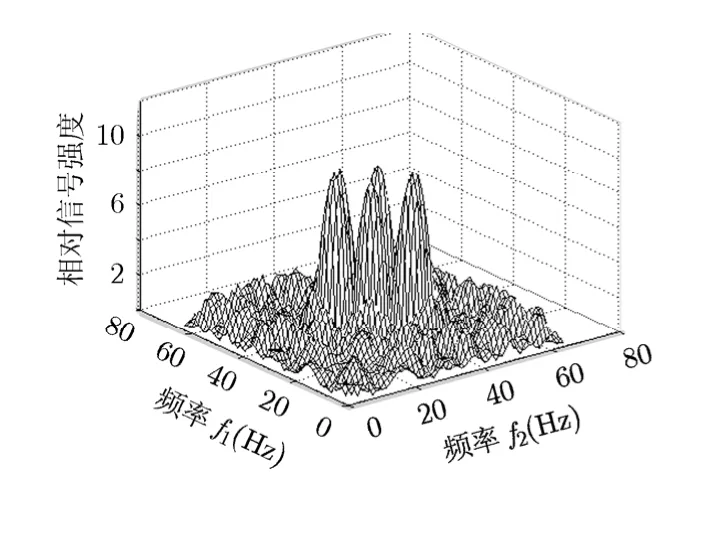
图6 BFFTAA-RAPF检测谱峰图

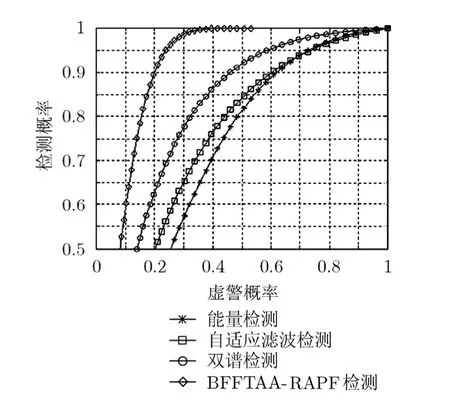
图7 SNR＝-13.2 dB时的4种检测方法的ROC曲线

[1] Jovicic A and Viswanath P. Cognitive radio: An informationtheoretic perspective[J]. IEEE Transactions on Information Theory, 2009, 55(3): 3945-3958.

[2] SafDar G A and Srinivasa S, et al.. Common control channel security framework for cognitive radio networks[C]. The IEEE 69th Vehicular Technology Conference, Barcelona,Spain, Spring, 2009: 102-108.

[3] Wang Xiao-yu, Wong A, and Ho Pin-han. Stochastic channel prioritization for spectrum sensing in cooperative cognitive radio[C]. The 6th IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, Jan. 2009:488-493.

[4] Kim Jae-moung, Sung Hwan, Sohn Ning-han, Zheng Guan-bo, Kim Young-min, and Lee Joo-kwan, et al..Cognitive radio software testbed using dual optimization in genetic algorithm[C]. The 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, CrownCom, 2008: 235-239.

[5] Kadhim D J, Liu Wei, and Cheng Wen-qing. Ultra wideband cognitive network objective issues [C]. FCC '09. International Conference on Future Computer and Communication,Wuhan, China, June 2009: 35-38.

[6] Cabric D, Mishra S M, and Brodersen R W. Implementation issues in spectrum sensing for cognitive radio[C]. the 38th Annual Asilomar Conference on Signals, System and Computers, Pacific Grove, CA, November 2004: 772-776.

[7] Gardner W. Signal interception: a unifying theoretical framework for feature detection [J]. IEEE Transcations on Communication, 1988, 36(8): 897-906.

[8] Golmie N, Chevrollier N, and Rebala O. Bluetooth and WLAN coexitence:challenges and solutions[J]. IEEE Wireless Communication Magazine, 2003, 10(6): 22-29.

[9] Simon Haykin. Cognitive radio: brain-empowered wireless communication[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220.

[10] Koivunen J. Spectrum sensing in cognitive radios based on multiple cyclic frequencies [R]. http://arxiv.org/abs/0707.0909v1.

[11] Kostylev V I. Engergy detection of a signal with random amplitude[C]. Proc. IEEE International Conference Communication, New York, 2002: 1606-1610.

[12] Eaddy J S D and Kadota T. On the approximation of the optimum detector by the energy detector in detection of colored gaussian signals in noise[J]. IEEE Transactions on Acustics, Speech, & Signal Processing, 1984, 32(3): 661-664.

[13] Kostylev V I and Slichenko M P. Energy detection of radio signals against the background of nongaussian noise with unknown intensity[J]. Radiophysics and Quantum Electronics,2009, 52(11): 822-831.

[14] Clark G A, Mitra S K, and Parker S R. Block implementation of digital filters[J]. IEEE Transactions on Circuit Theory,1981, 28(6): 584-592.

[15] Hu Chia-chang and Jhu Wei-ciao. Adaptive block DFT-LMS signal detection in ultra-wideband communications[C].Proceedings of the 6th IEEE Conference on Consumer Communications and Networking Conference. Las Vegas, NV,USA, 2009: 543-544.

[16] Atrouz B, Alimohad A, and issa B A. An effective jammers cancellation by mean of a rectangular array antenna and a sequential block LMS algorithm: case of mobile sources[J].Progress in Electromagnetics Research C, 2009, 7(3): 193-207.

[17] Nikias C L and Mendel J M. Signal processing with high-order spectra[J]. IEEE Signal Processing Magazine, 1993,7(5): 10-38.

[18] Wu Chang-qi, Tian Yuan, and Han Xiu-feng. Carrierfrequency capture base on bispectrum estimation under extremely low SNR and large doppler frequency shifting[J].Electronic Technology, 2009, 36(8): 73-75.

[19] Slepian D. Some comments on the detection of gaussian signals in gaussian noise[J]. IEEE Transcations on Information Theory, 1958, 4(3): 65-68.

[20] Tandra R. Fundamental limits on detection in low SNR[D].[Ph.D. dissertation], University of California, Berkeley, 2005.