最小化路径代价和流量均衡模型及算法

杨华卫 王洪波 程时端 陈山枝 林 宇

①(北京邮电大学网络与交换技术国家重点实验室 北京 100876)②(电信科学技术研究院无线移动通信国家重点实验室 北京 100083)

1 引言

随着IP网络规模的快速增长和流量请求的迅速增加，网络流量的不均衡分布日趋明显：局部网络链路出现拥塞的同时，网络其余链路轻载或空闲的情形却普遍存在。在网络硬件快速发展的情形下，高速的交换和路由单元以及大容量的网络链路使得运营商可为网络大量增加硬件资源。但这种带宽过量供给的方式是以网络资源低利用率为代价的，并不能有效地解决热点链路的拥塞问题。流量工程通过控制路由实现流量的优化分布[1]，在提高网络资源利用率的同时减少网络拥塞。根据网络拓扑和流量矩阵[2]建模后，得到优化的路由，直观而言，就是把流量分布到带宽允许的路径上，并达到流量的均衡。

文献[1]从不同角度对流量工程中的路由算法进行了划分，从中可见，现有的流量均衡模型按路由优化目标可分为两类：最大链路利用率最小化模型以及最小化链路代价和模型，下面就两类模型分别描述。

文献[3]为流量工程中的流量均衡首次提出叠加式(overlay approach)的显式路由算法，与基于目的地址的路由相比可更有效地提高网络利用率，文中最基本的问题是在满足流量请求的情形下优化网络性能，模型的目标即是最小化拥塞和最大化流量承载潜力。文献[4]提出通过集成式(integratedapproach)的网络路由方式优化流量分布，同时指出了通过合理设置链路权值，显式路由在理论上转化为最短路径的可能性。文献[5]给出了约束路由的流量均衡算法，这是MPLS路由在大规模网络中建立路径的数目受限情形下提出的。上述的模型或算法为避免拥塞采用优化最大链路利用率的方式来达到流量的均衡分布。最小化最大链路利用率是流量工程中均衡流量分布的直观算法，其优点是建模过程中优化目标简单、易于获得最优解，其缺点是未从整体网络的角度考虑流量均衡。

文献[6]为一般路由优化建立了基本数学模型，流量可在网络OD(Origin-Destination)对的所有路径间任意分布；其中引入了流量通过链路的路由代价函数，以惩罚高负载链路传送流量的路由方式。文献[7]正式提出基于IP路由协议的流量工程，并探讨了OSPF(Open Shortest Path First)和IS-IS(Intermediate System to Intermediate System)的应用。文献[8]总结了调整路由协议参数的优化模型和算法，使得不关注网络流量的传统路由协议可以通过优化参数而均衡分布流量。上述模型和算法把网络看作所有链路的综合，在考虑流量均衡分布时，优化的结果是选择使得所有链路路由流量代价和最小的流量分布。这类模型尽管避免了最小化最大链路利用率模型的缺陷，但他们考虑的是链路路由流量的代价，而非路径路由流量的代价。

本文认为，网络中流量分布的均衡性决定于路由时各路径间流量的分配，而路径上分配的流量又决定于该路径路由流量的代价。为此，本文提出了最小化路径代价和模型，它的优化目标是流量请求在所有可用路径上路由流量的路径代价和最小化，并且定义路由流量的路径代价为路径上瓶颈链路路由流量的代价。随后，本文提出利用负价环算法求得流量的最优网络分布，并通过实验证了该模型可显著降低网络最大负载链路的利用率。

本文的内容安排如下，第2节描述本文提出的流量均衡模型，实验和相关的验证在第3节讨论，最后总结全文并提出待研究问题。

2 最小路径代价和模型

本节假定流量矩阵已知，建立网络中所有路径间均衡分布流量的优化模型，并在负价环算法基础上实现优化流量分布的路径路由算法。

2.1 网络模型

IP网络以有向图G(N,A)表示，N是路由器的集合，A是路由器间有向链路的集合。有向链路的容量c(a)定义为链路可承受流量的最大带宽。流量矩阵D给出每个OD对(s,t)间要求传送的流量请求。那么路由问题即可定义为非零D(s,t)在s到t的路径间的流量分布。

流量路由结果用一个矩阵R表示，其中链路a上负载D(s,t)的流量比例表示为R(s,t,a)。那么链路a上的负载即可表示为其带宽利用率为l(a)/c(a)。

2.2 既有流量均衡模型

最小化最大链路利用率优化模型，其优化目标是最小化maxa∈A(l(a)/c(a))，即对网络中最大利用率的链路进行优化。这个优化目标的优点是直观、比较容易实现，其缺点是只对最高利用率链路优化，在该链路无法进一步优化(如最高利用率链路为流量必经的瓶颈链路)时，不关心其余链路的流量优化。

文献[3,8]克服了最小化最大链路利用率模型的缺陷，提出流量路由的最小化链路代价和模型，其优化目标是最小化其中的代价函数φ()是链路利用率的函数，为惩罚路由方案中的高负载链路情形，函数定义为分段线性递增凸函数。文献[6]从分组级别解释了模型中流量路由的方式，当分组经过从s到t的一条路径时，要为路径中的每个链路付出路由代价，那么，Φ即是所有分组路由时的路径代价之和。为引述方便，下文中称该模型的流量路由算法为最小代价路径(Minimal Cost Path, MCP)路由优化算法，其中的路径代价是路径上所有链路代价之和。

最小化链路代价和模型以路径上链路代价之和作为流量路由时的路径代价，在这样的路径代价定义下，可能导致下述的流量分布不均衡现象。路径p1包含拥塞链路，p2为无拥塞链路，在前者的路径代价较小时，分组将优先选择路径p1；而这样的选择更加重了路径p1上拥塞链路的负担。在链路利用率比较均匀时，路径上链路的数目成为路径代价的主要影响因素；显然，跳数少的路径更具吸引力，使得短路径趋向满载的几率比长路径更大。

下面示例MCP算法在分布流量时引起流量不均衡分布的情形。图1是一个简单的网络拓扑，在结点(s,t)间有两条路径p1(s, l, n, t)和p2(s, l, m, n, t)。假设链路容量c(a)=200,∀a∈G，在流量请求D(s,t)从0递增到200的过程中，按照最小化链路代价和模型中的φ()函数对流量请求在路径p1和p2间分配，两条路径上的流量负载之比l(p2)/l(p1)随流量增加的变化趋势如图2所示。

由图可见，在流量加载的前半段，两条路径的负载差别较大，p2的负载接近于p1负载的1/2；在流量递增的后续过程中，流量在两条路径间的分布无确定趋势。在既定路径代价定义下，MCP算法在路径间分布流量时均衡性明显不足，而这对避免网络拥塞和提高网络容纳未知流量的能力是极其不利的。

图1 两条路径的简单拓扑

图2 路径负载对比曲线

2.3 最小路径代价和模型

由于最小化链路代价和模型和MCP路由优化算法存在缺陷，要实现流量的均衡分布、最小化网络拥塞，必须构造新的优化模型，实现相应的优化算法。本文的观点是流量在各路经间的均衡分布决定了网络流量分布的均衡性，亦即网络的拥塞特性；流量在路径间的均衡分布是与路径的拥塞特征相关的，而路径的拥塞特征取决于路径上瓶颈链路的拥塞特征。

下面再次以图的拓扑为例说明，其中各链路容量c(a)=200,∀a∈G，并有背景流量l(m, n)=40，其余链路均无背景流量，并假定(s,t)间的流量请求D(s,t)=100。

根据MCP算法，链路(lm)(mn)(ln)剩余容量满足要求时，流量分布如图3所示，(lm)和(mn)的链路代价和与(ln)的链路代价相等(值是90.8)。在图3中，由于(mn)上背景流量的存在，使得(mn)成为路径(lmn)的瓶颈链路。根据本文观点，(mn)的拥塞特征决定了路径(lmn)的拥塞特征，即在路径(lmn)和(ln)间分布流量时应按照他们的瓶颈链路(mn)和(ln)(单链路构成的路径)的拥塞特征分布流量，这时，合理的新的流量分布如图4所示。

比较图3和图4的流量分布，网络的流量分布均衡性比较如表1所示，其中链路负载最大差是拓扑中最大链路负载与最小链路负载之差，可见新的均衡分布的优越性。

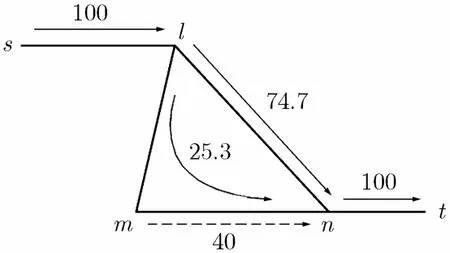
图3 MCP算法流量分布

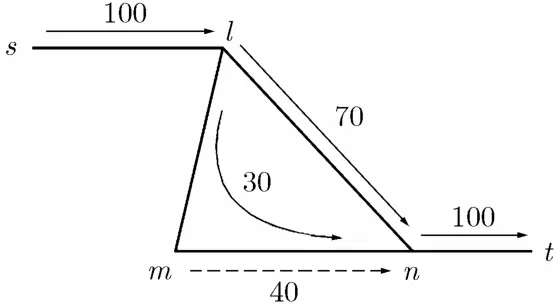
图4 新的均衡流量分布

表1 流量均衡方式对比

因此，本文提出最小化路径代价和流量均衡模型，定义路由流量的路径代价为路径上瓶颈链路路由流量的代价，其优化目标是路由所有流量请求的路径代价和最小化。

定义 设p为(s,t)间任一路径，链路ak∈p，并且l(ak)/c(ak)=maxa∈p(l(a)/c(a))，即ak是p上的瓶颈链路，那么，p的路径代价就定义为φp≜φ(l(ak)/c(ak))。

在定义流量经过路径p路由的路径代价φp后，就可以建立网络流量均衡的优化目标了。假设，P(s,t)为(s,t)间所有路径的集合，则(s,t)间路径间分布流量的路径代价和就是。那么，网络的流量均衡是最小化分布所有流量的路径代价和，最小化目标如公式(1)所示。

为取得上述目标下的最优流量分布，本文在负价环算法[9]基础上提出了基于瓶颈链路的最小代价路径(Bottleneck-based Minimal Cost Path, BMCP)路由算法。该算法的基本思想是：(s,t)间存在两条以上路径时，总有改变D(s,t)在这些路径间分配流量的可能性，这种改变使得流量路由的路径代价和发生改变，而代价和最小的分配方式才是最优的流量分布。下文简要介绍负价环算法后，描述BMCP算法。

2.4 负价环算法简介

因在流量均衡算法中的应用，下面简要介绍负价环算法。有向图G(N,A)表示一个通信网，ai,j是ni到nj的有向边，边的容量是ci,j，边上的实际负载是li,j。在单源s单宿t情形下，一个大小为Fs,t的流量请求在网络中分布必须满足下列条件：

(1)非负性和有限性：

(2) 连续性：

共|N|−1个限制条件，满足这些条件的流量分布称为一个可行流。

在保持总量Fs,t不变的情况下，给出一个初始可行流，按链路上的负载和容量作出G(N,A)的补图，补图上若存在一个有向环，并且各边的费用之和为负，则称为一个负价环。沿负价环方向增流，并不破坏环上各结点的流量连续性，也不破坏各边的非负性和有限性，结果得到一个总费用降低的新可行流。

负价环算法步骤归纳如下：

(1)在图上找到任一可行流作为初始可行流。

(2)在图上做补图。

(3)在补图上找负价环，若负价环则算法终止，若有则沿负价环方向增流。

(4)修改原图各边负载，返回(1)。

2.5 BMCP流量均衡算法

本节的流量均衡算法BMCP建立在负价环算法基础上，由于应用环境的改变做了适应性的改变，下面先定义路径负价环。

定义：同一流量请求在网络中形成的路径集合，按路径上瓶颈链路的负载和容量求补图，如果补图上存在一个有向环，并且这个环流量的路径代价和为负，则称为一个路径负价环。

那么BMCP算法把流量请求分布到网络上的算法基本步骤如下：

(1)TM[m][n]内保存网络流量请求数据；

(2)graph保存网络拓扑；

(3)初始化一个可行流，参数是graph和TM；

(4)for (i=0, j=0; i＜m, j＜n; i++, j++){

(5) pathset = OD对(i,j)间的路径；

(6) graph1=由pathset生成的子图；

(7) while(true){

(8) pathneckset = OD对(i,j)间路径上瓶颈链路；

(9) graph2 = 由graph1和pathnecknet生成的补图；

(10) if !getNCostLoop(graph2)//补图中已没有路径负价环

(11) break；

(12) delta = 增流量；

(13) 用delta值更新graph1的链路负载；

(14) }

(15) }

3 模型及算法验证

为验证最小化路径代价和模型和BMCP路由算法的有效性，本文采用了Abilene2的网络拓扑，如图5所示(结点从0到11编号，其中0和1结点位置相同)，除了结点0和1间的双向链路带宽为2.5 G之外，其余双向链路带宽均为10 G。并采用Zhang在Abilene2网络采集的24周流量数据[10]，流量采集的时间粒度是5 min，即每天产生288个流量矩阵。

图5 Abilene2网络拓扑

本文进行了3次实验，在实验中着重考查了BMCP算法和MCP算法在流量均衡分布中调控能力的对比(由于最小化最大链路利用率优化算法较MCP的明显劣势，详见2.2节，文中不与该模型作对比实验)。实验以流量优化后的最大链路利用率(Maximum Link Utilization，MLU)作为流量分布均衡性的指标，下文描述各实验的详细过程和结果分析。

3.1 实验1

为了观察BMCP路由优化算法在网络流量变化过程中对流量均衡性的控制能力，本文选择了24周数据中的两个48 h数据分别进行了实验，数据信息如表2所示。

由于最终流量分布的均衡性完全由BMCP算法在流量分布时选择的路由决定，实验中流量分布时把每个流量请求分割成若干个流，流大小符合重尾分布[11]，在加载流时选择随机序列。在实验中，流量矩阵间的分布是独立的，BMCP算法分布流量时的基本步骤如下：

表2 实验数据描述

(1)读取流量矩阵；

(2)为每个流量请求生成重尾分布特征的网络流；

(3)对所有流量请求的网络流随机排序；

(4)取出下一个网络流；

(5)以BMCP算法选择路径并加载该网络流；

(6)更新所选路径上所有链路的网络流数据；

(7)如果还有待分布的网络流，转到(4)。

MCP算法与BMCP算法的实验步骤相同，只是在选择路径时采用MCP算法(仅步骤(5)不同)，而且采用相同的网络流分布和加载序列。

实验结果如图6，图7所示，横轴的每个时间点对应一个流量矩阵，纵轴对应这个流量矩阵分布后网络中的最大链路利用率，结果分析见表3。

表3 实验1MLU相对差分析

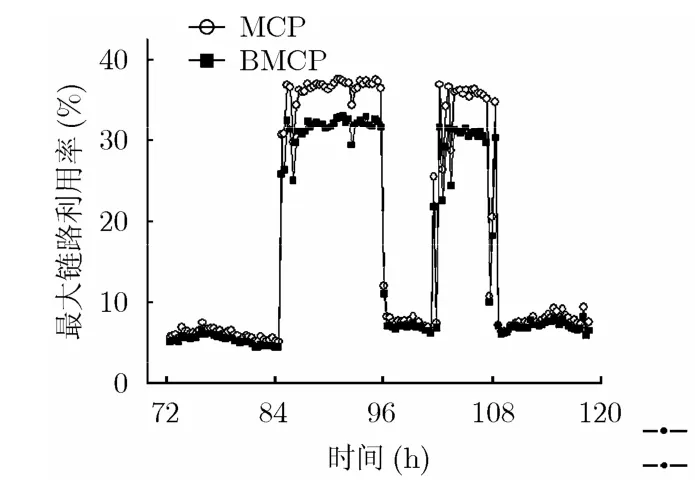
图6 实验1(I)最大链路利用率

图7实验1(II)最大链路利用率

表3是MCP算法下MLU最大位置时，BMCP算法对同一流量矩阵分布后的结果比较，从中可见两次实验中MLU下降相对差分别达到19.2%和17.1%。

3.2 实验2

该实验是在给定初始流量矩阵后，考查BMCP算法在关键流量请求增大时对网络最大链路利用率的优化作用，其中的关键流量请求是指对网络最大链路利用率起关键影响作用的流量矩阵元素。在实验中，关键流量请求逐步递增，直到网络最大链路利用率最终达到100%，实验的数据信息如表4所示。

表4 实验数据描述

实验结果曲线如图8。为更清晰地分析图8的数据，根据图中的纵轴数值(即流量优化后的MLU)计算差值的百分比，得到图9的曲线。可见，在关键流量请求逐渐增加的过程中，与MCP算法相比，BMCP算法降低最大链路利用率的相对百分比均值达12.1%。

从图8和图9可见，网络最大链路利用率在49%-81%间时，MLU相对差值较大，最大达到16.9%。即网络负载较重时，OD间普遍存在可用的轻载路径，BMCP算法可有效控制网络的拥塞；而在最大链路利用率继续增加时，OD间的所有路径趋于满载，两种算法都将无力控制网络逐渐拥塞的趋势。

图8 关键流增长时MLU优化对比

3.3 实验3

本实验考查流量递增初始阶段，BMCP对网络流量均衡的控制能力，是实验2的补充。类似实验2，通过非关键流量请求的逐渐递增，验证BMCP算法调控网络均衡性的能力，并与MCP算法做了比较，其实验数据如表5所示。

表5 实验数据描述

结果数据绘制成曲线，如图10。从中可见，非关键流量请求在流量初始分布时，并不影响整个网络的最大链路利用率，随着该流量请求的增加，成为关键的流量请求；同时，无论选定流量请求是否是关键流量请求，BMCP算法与MCP算法相比都有显著优势。

图11是对图10的纵轴数据(即流量优化后的MLU)计算相对差后绘制的曲线，在流量请求开始主导网络最大链路利用率后，MLU相对差呈明显的上升趋势，显示BMCP算法相对于MCP算法可更好地抑制网络拥塞。

图9 关键流增长时MLU相对变化

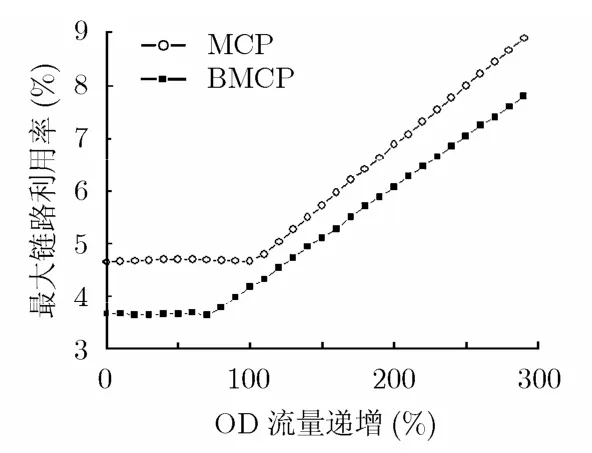
图10 非关键流增长时MLU优化对比

图11 非关键流增长时MLU相对变化

4 结束语

尽管运营商在网络工程中有带宽过量供给的趋势，但这种以资源低效利用换取服务质量的措施并不能从根本上解决网络拥塞。网络拥塞往往是流量请求汇聚的结果，而相对空闲的链路并未受到这些流量的青睐，旁路拥塞链路上的流量到空闲路径上同时保证资源的有效利用是本文的研究主题。

为了最小化网络拥塞，本文在指出网络拥塞决定于流量路由时所选路径的拥塞特征后，建立了流量分布的最小路径代价和模型。在流量路由选择路径时，以负价环算法为基础，提出基于瓶颈链路的最小代价路径路由算法。实验验证了该模型和算法的有效性。在实际的流量工程中，该模型的流量分布结果可作为评价依据；因流量矩阵的全局特性，该模型在集中式的流量工程中更有优势。

本文在优化流量分布时，未把服务质量要求作为约束条件，原因是实践中的流量质量要求因业务类型而异，而且满足服务质量的流量分布往往与流量均衡目标相悖。随着覆盖网络发展，其自私特性的网络流量对流量分布的动态适应能力提出了更高要求。我们将在这方面开展进一步的研究工作。

[1] Wang N, Kin H, and Pavlou G, et al.. An overview of routing optimization for internet traffic engineering[J]. IEEE Communications Surveys & Tutorials, 2008, 10(1): 36-56.

[2] Rincon D, Roughan M, and Willinger W. Towards a meaningful MRA of traffic matrices[C]. Proceedings of the 8th ACM SIGCOMM Conference on Internet measurement,Vouliagmeni, Greece, 2008: 331-336.

[3] Wang Y and Wang Z. Explicit routing algorithms for internet traffic engineering[C]. Computer Communications and Networks, Boston, MA, USA, 1999: 582-588.

[4] Wang Y, Wang Z, and Zhang L. Internet traffic engineering without full mesh overlaying[C]. IEEE Infocom Proceedings, Anchorage, Alaska, USA, 2001, 1: 565-71.

[5] Cugola G and Nitto E. On adopting content-based routing in service-oriented architectures[J]. Information and Software Technology, 2008, 50(1-2): 22-35.

[6] Fortz B and Thorup M. Internet traffic engineering by optimizing ospf weights[C]. IEEE Infocom Proceedings, Tel Aviv, Israel, Aug, 2000, 2: 518-528.

[7] Fortz B, Rexford J, and Thorup M. Traffic engineering with traditional ip routing protocols[J]. IEEE Communications Magazine, 2002, 40(10): 118-124.

[8] Resende M and Pardalos P. Handbook of Optimization in Telecommunications[M]. New York, Springer Science +Business Media, 2006: 679-700.

[9] Ahuja R, Magnanti T, and Orlin J. Network Flows: Theory,Algorithms, and Applications[M]. New Jersey, Prentice Hall,2005: 294-356.

[10] Zhang Y. 6 months of Abilene traffic matrices. Http://www.cs.utexas.edu/～yzhang/, 2009.

[11] Kundu S, Pal S, and Basu K, et al.. An architectural framework for accurate characterization of network traffic[J].IEEE Transactions on Parallel and Distrituted Systems, 2009,20(1): 111-123.