基于虹膜信息的身份签名方案

赵泽茂 王向阳 许春根

①(杭州电子科技大学通信工程学院 杭州 310018)②(南京理工大学应用数学系 南京 210094)

1 引言

自Shamir在1984年提出了基于身份的密码体制的概念以后，基于身份的加密和签名方案相继被提出。在基于身份的密码体制中，用户的公钥可以是用户的姓名、地址、E-mail、身份证号码等，用户的私钥则由可信任的认证中心(CA)产生。显然，公钥不证自明，大大减少密钥的认证复杂度，不存在由CA颁发公钥证书所带来的存储和管理开销的问题，有关基于身份的密码体制的研究进展见参考文献[1]。

生物特征在以其独特的优势广泛应用于网络身份认证。目前，对生物特征的研究主要集中在两个方向：一是基于传统的生物特征识别技术，如指纹识别技术等，现已发展成相当成熟的实用技术；二是基于生物特征的密钥产生技术，这是目前研究的热点问题之一。前者主要用于身份认证，后者必须解决生物特征信息的模糊性与密钥的精确性之间的矛盾。文献[2-4]研究了如何从生物特征中提取公钥或私钥的问题，其中文献[4]引入的模糊机制最为实用，它把生物特征的模糊性与密钥的精确性有机地统一起来。利用生物特征设计数字签名的研究成果很多，如文献[5-7]。在基于身份的加密中，接收者的隐私性也受到了广泛关注，于是匿名的基于身份加密(Identity-Based Encryption，IBE)的概念就被提了出来[8]，随后，2008年，Boneh and Hamburg在Asiacrypt2008上给出了广义的基于身份的加密的方案[9]，文献[10]将指纹特征用于加密和认证方案的设计，文献[11] 提出一个基于身份的无需第三方可信任的密钥产生(Private Key Generation，PKG)系统的签名方案，2009年，文献[12]提出基于多重生物特征身份的签名方案。相比于其他的生物特征信息而言，虹膜信息构造公钥具有以下几点好处。首先，可节约时间和空间。因为虹膜信息具有人体所固有的唯一性且可直接提取，用户无须向权威机构证明自己的身份。其次，可进一步提高系统的安全性和可靠性。因为虹膜无法复制，失窃或被遗忘，且噪音引起的误差干扰相对较小。在这些基于生物特征信息构造的加密和签名方案中，普遍没有考虑到单个PKG系统可以随意伪造用户签名的安全隐患。本文提出的基于虹膜信息的签名方案引进两个PKG系统，主要是为了弥补单个PKG系统中随意伪造用户签名的缺陷，在随机预言机模型下，证明了该方案可抵抗在适应性选择消息和身份下的存在性伪造攻击，并能有效抵抗“生日攻击”。

2 预备知识

2.1 双线性映射

设G1是一个由P产生的循环加法群，它的阶为q，G2是一个阶为q的循环乘法群，q为大素数，假定在G1, G2上的离散对数问题(DLP问题)都是困难问题。双线性映射是指具有下列性质的一个映射: G1×G1→G2。

(1)双线性：对任意的P, Q, R∈G1；有对任意的a, b∈；有(aP, bQ)=(P, Q)ab。

(2)非退化性：存在P, Q∈G1，使得e(P, Q)≠1。

(3)可计算性：对于P, Q∈G1，存在一个高效的算法计算e(P, Q)。

本方案依赖以下困难性问题。

(1)离散对数问题(DLP)：对给定的Q=nP∈G1，求n∈。

(2)双线性对求逆问题：已知a=e(P, Q)，给定P∈G1，求Q∈G1。

(3)计算Diffie-Hellman问题 (CDHP)：对a, b∈，给定P, aP, bP∈G，计算abP。1

(4)判定Diffie-Hellman问题 (DDHP)：给定P, aP, bP, cP∈G1，其中a, b, c∈，判定c≡abmod p是否成立。

(5)间隙Diffie-Hellman问题(GDHP)：在群G1上，DDHP易于解决而CDHP难以解决，则称此群为间隙Diffie-Hellman群。

2.2 基于随机问答器攻击模型定义

基于身份的数字签名的基于随机问答器攻击模型是由Cha和Cheon[13]给出的攻击模型补充得到的。

设Sim为攻击算法，C为预言机，它们参与如下游戏G。

(1)预言机C运行Setup，并发送系统参数SP给Sim。

(2) Sim可以向预言机C请求如下的服务。

(a)身份Hash函数H1服务：对于Sim给出的任何身份ID，C计算H1(ID)并将其发送给Sim。

(b)Extract服务：对于Sim给出的任何身份ID，C运行Extract得到对应于ID的私钥并将其发送给Sim。

(c)询问Hash函数H2服务：对于Sim给出的任何消息m和U∈G1，C计算H2(m, U)并将其发送给Sim。

(d)Signing服务：对于Sim给出的任何身份ID和消息m，C返回对应于ID和消息m的签名给Sim。

(3)最后Sim输出签名(ID,m, U, E, V)，其中ID未向Extract询问过，(ID,m)未向Signing询问过。

称Sim赢得游戏当且仅当(ID,m, U, E, V)能通过Verification的验证。

一个由Setup，Extract，Signing和Verification等4个算法组成的基于身份的数字签名方案，如果不存在多项式时间算法Sim以不可忽略的优势赢得游戏G，则称该方案在适应性选择消息下能抵抗伪造攻击。

3 虹膜信息的提取与嵌入

3.1 虹膜信息的模糊提取

[3]，虹膜信息的提取过程如图1所示。

虹膜图像采集：通过虹膜采集设备获取虹膜图像。

虹膜图像预处理：虹膜图像预处理算法主要解决虹膜图像的平移、瞳孔的缩放和光照不均等原因对识别结果产生的干扰，以获得纹理清晰便于识别的虹膜图像。该算法主要进行虹膜内外边缘定位、归一化和图像增强等。

虹膜特征提取与编码：虹膜特征提取与编码是整个过程最关键的一步。特征提取主要包括图像有效区域选择和滤波器的设计，经过滤波器后可提取一系列表示虹膜图像纹理特征的参数，这些参数最终编码成表示虹膜纹理的n位特征码h。

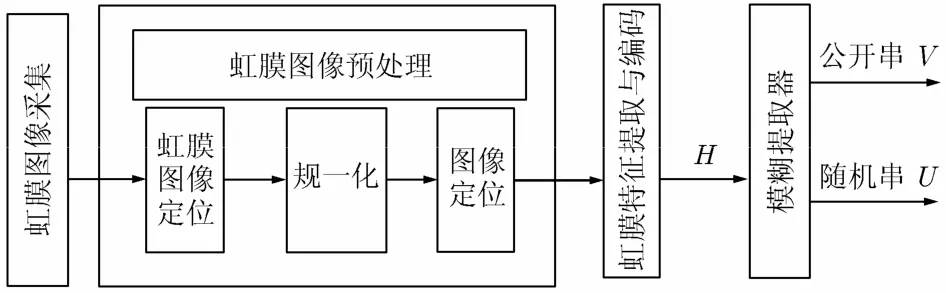
图1 虹膜信息的提取过程框图

模糊提取器[3]：输入虹膜特征编码h，得到随机串U和公开的串V。模糊提取器可以容忍一定数量的错误，即如果输入h轻微的变化为h'，输出的随机串U是一样的。Dodis等人[2]定义了函数Gen和Rep来构建模糊提取器，函数Gen是输入虹膜特征编码h，输出随机串U和公开的串V，函数Rep是输入h'和公开的串V恢复随机串U，如图2所示。

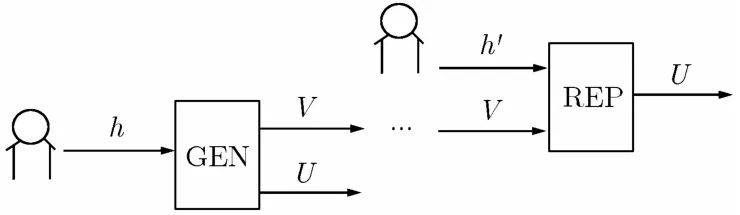
图2 函数Gen和Re p示意图

现在使用汉明距离度量在M={0,1}k空间中构建一个模糊提取器(M, k, t)。定义kbit 的纠错编码函数Ce:M→{0,1}k，解码函数Cd:{0,1}k→M 。函数Gen(h)输出参数U∈{0,1}k，且V=b⊕Ce(U)。同样，Rep(h',V)=Cd(V⊕h')=U 当且仅当dis(h,h')≤t。在此过程中，只需提供虹膜信息就可以生成和恢复随机串U，无需密钥介入。

3.2 将虹膜信息嵌入到椭圆曲线

为了将输出串U嵌入到椭圆曲线中，使用一个标准哈希函数H，即安全哈希算法SHA-1，先将输出串U映射到集合A={0,1}160上，这与文献[3]相同。然后使用一个嵌入函数g将160位字节串A映射到G上，其中G是椭圆曲线E(Fp)上的点组成的一个子群。即Pu=g(H(U))，其中Pu是对应串U的点。

字节串U=U1U2…Uk嵌入到椭圆曲线上Pu点可采用如下方法。

(2)转换X1到椭圆曲线的点(XP,YP)：首先计算α=+aX+bmod p ，然后计算αmodp的平方1根。如果存在平方根，则XP=X1，=αmodp ，点Pu=(XP,YP)，否则计算X1=X1+i ，(i为预先根据实际设定的比较小的整数值，如i=1)，重复步骤(2)，直到找到点Pu=(XP,YP)。

4 基于虹膜信息的签名方案

基于虹膜信息的签名方案，与普通的基于身份签名方案相比，系统还包括一个虹膜库，用来存放签名者的虹膜数据，虹膜库由验证者来保管。参考文献[2]，为了避免单个PKG有太大的权力随意伪造签名者的签名，本方案引进了两个独立的密钥生成机构PKG1和PKG2。该方案包括系统建立，密钥生成，签名算法和验证算法等4个算法。

系统参数建立：设G1, G2分别是加法群和乘法群，阶为q，且在G1, G2中离散对数问题都是难解的。设e是由椭圆曲线上的Weil配对派生得到G1×G1到G2的双线性映射，H1:{0,1}*→G1, H2:{0,1}n×G2→Zq*，是两个公开的单向加密Hash函数，其中H1是标准哈希函数SHA-1，是哈希函数H:{0,1}*→{0,1}160和嵌入函数g :{0,1}160→G1的组合，即H1(U)=g(H(U))。PKG1和PKG2分别独立随机选取s1∈R和s2∈R作为系统私钥，计算Ppub1=s1P 和Ppub2=s2P作为系统公钥，公开系统参数为

用户密钥生成：假设用户给出的虹膜特征信息h∈M，两个PKG首先利用模糊提取器(M, k, t)中的Gen函数输出参数U∈{0,1}k和V=h⊕Ce(U)∈{0,1}n。然后分别计算A的公钥QA=H1(U)∈G1和部分私钥SAi=siQA,(i =1,2)。最后通过安全信道分别将私钥传送给用户，并公开串V。

签名算法：设m∈{0,1}*为待签名的消息，用户A签名过程如下：

(1)任意选取两点P1, P2∈G1，计算r1=e(P, P1),r2=e(P, P2)；

(2)计算v1=H2(m, r1),v2=H2(m, r2)；

(3)计算w=P1+v1SA1+v2SA2；则(w, v1, v2)为用户A对消息m∈{0,1}*的签名。验证算法：验证者收到用户A的签名后，为了验证用户A对消息的签名(w, v1, v2)，提取用户A的虹膜信息H'∈M，使用模糊提取器(M, k, t)中的Rep函数恢复串U，当且仅当dis(h, h')≤t时，计算

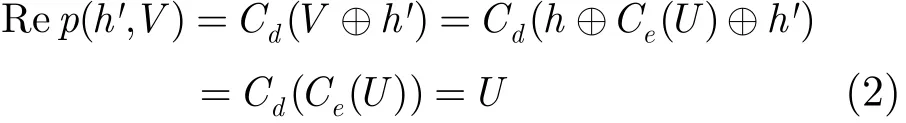
然后计算QA=H1(U)∈G1，和r1=e(w, P) e(QA,−Ppub1)v1e(Q,A−Ppub2)v2，最后检查v=H(m, r)是否成立？当且仅当等式成立签名有效。

本方案是正确的。因为

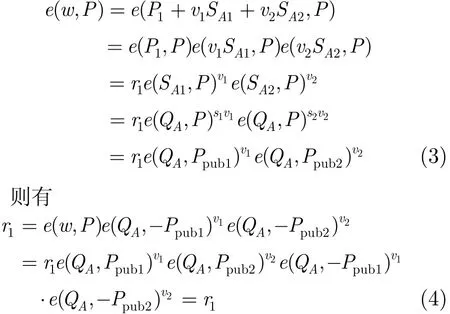
即等式v1=H2(m, r1)成立。

5 安全性分析

定理1 本方案在一定程度上消除了单个PKG可以任意伪造签名的安全隐患。

证明 公钥由签名者的虹膜数据生成，任何攻击者无法伪造。只有输入模糊提取器的虹膜数据与库中的虹膜数据差别不大的时候，才可以计算签名者的公钥，才可以利用其公钥验证签名方案。而且，本方案引进了两个独立的PKG，每个PKG只能生成用户的部分私钥，所以单个PKG并不能伪造签名者的签名，除非两个PKG联合攻击。所以，本方案在一定程度上消除了单个PKG可以任意伪造签名的安全隐患。

定理2 在随机预言机模型下，本方案在选择性消息和身份下是不可伪造安全的。

证明 若攻击者C能以不可忽略的概率在小于时间T经qs次签名提问和qh次Hash提问伪造本方案，且通过了验证方程赢得游戏G，则可以构造一种算法Sim在小于时间T'计算y=e(Q, P)中Q，即计算出双线性对求逆问题。根据双线性对求逆问题困难性，不存在多项式时间算法Sim以不可忽略的概率伪造本方案而赢得游戏G，即本方案在随机预言机模型下，在选择性消息和身份攻击下是不可伪造的。

设G1是加法循环群，阶为q，其生成元为P∈G1，构造Sim算法，给定一个双线性映射e，在适应性选择消息和身份攻击下，如果攻击者C能以不可忽略的概率伪造本方案，则构造算法Sim的目标是计算y=e(Q, P)中Q。

U-Hash(H1)提问：系统维护一个由(Ui, Qi)(其中1≤i≤qh1)构成的H1表。当攻击者C提问虹膜数据Ui，若(Ui, Qi)∈H1表，系统用Qi回答，否则，系统随机选取λi∈，计算：Qi=λiP，用Qi回答，并添加(Ui, Qi)到H1表，并相对应保存λi。

消息-Hash(H2)提问：系统维护一个由(mj, rj,vj)(其中1≤j≤qh2)构成的H2表。攻击者C提问(mj, rj)，若(mj, rj, vj)∈H2表，用vj作答，否则，系统随机选取αj∈，令vj=αj作为回答，并添加到H2表。

签名提问：攻击者提问对消息mg的签名，系统在H1表中搜索(Ug, Qg)，在H2表中搜索两组(mg1,rg1,vg1),(mg2,rg2,vg2)。系统选取点Pg∈G1，令rg1=e(P, Pg)，wg=Pg+vg1λgPpub1+vg2λgPpub2，签名回答为(wg, vg1,vg2)。

因为

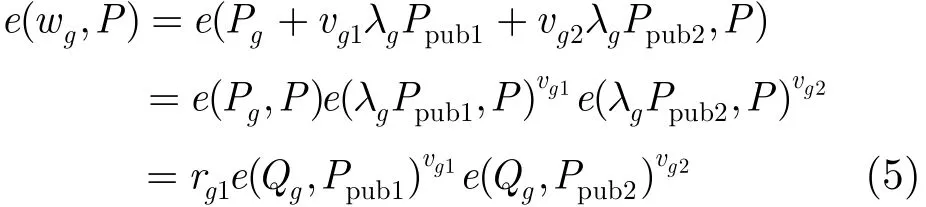
输出 攻击者C与U-Hash(H1)预言机、消息-Hash(H2)预言机、签名提问预言机联合，以不可忽略的概率输出对消息m伪造签名(wg, vg1,vg2)。

利用重放技术，Sim算法可得到对消息的两个有效伪造签名(w, v1, v2)和(w′, v1′,v2′)，两个签名的验证等式为

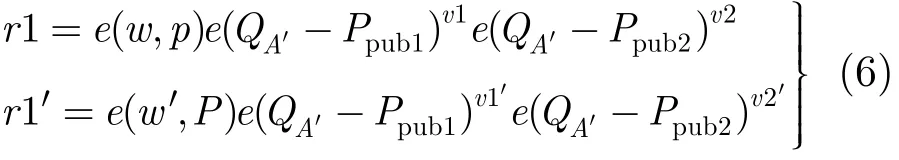
若在签名提问中两次选取的P是相同的，则r1r1′=，则通过两个验证等式可得到可知，随机选择v1, v2,v1′,v2′，可相应的得到

即成功的计算出了y=e(Q, P)中Q。由双线性对求逆问题困难性可知，不存在多项式时间算法Sim以不可忽略的概率伪造本方案，即在随机预言机模型下，该方案在选择性消息和身份下是不可伪造安全的。

定理3 本方案可以有效抵抗“生日攻击”。

证明 签名时P是从G1中随机选取的，选中G1中任一元素的概率均为1/q。随着签名次数的增加，出现相同的P的概率将会大大提高。这就是所谓的“生日问题”。“生日问题”是说：在23个人中出现两个人生日相同的概率就会大于0.5。其计算公式是：在一个有m个人的集体里，至少两人的生日在同一天的概率为p=1−365m。同样地，在方案中，从G1中随机取元素，在取了m次后，出现相同元素的概率为p=1−。要使概率p大于0.5, m大约取就行了。可见“生日攻击”比直接求离散对数更容易破解签名私钥，这样就大大降低了签名方案的安全性。

假设攻击者在本方案中获得签名人对消息的两个签名(m, w, v1, v2)和(m',w',v1',v2')，且消息的签名选择了相同的点P1, P2，即两个签名具有相同的r。根据签名算法有：w=P1+v1SA1+v2SA2,w'=P1+v1'SA1+v2'SA2，在这两个等式中含有3个未知数(P1, SA1,SA2)，因而，攻击者无法求解出SA1和SA2，即攻击者无法获得签名人的私钥，从而攻击者无法冒充签名者对任何消息的签名。“生日攻击”对本方案不起任何作用。

6 结论

由于基于身份的公钥密钥系统避免了基于证书的公钥密码系统中繁琐的证书管理，在实际应用中比较方便快捷，同时使用虹膜信息作为身份可以节省许多空间和时间。本方案利用虹膜信息构造公钥，将虹膜信息应用于签名方案中，提出一种基于虹膜信息的身份签名方案。该方案引进了两个PKG，防止单个PKG随意伪造签名，且在随机预言机模型下，具有在选择性消息和身份下的不可伪造安全，并能有效抵抗“生日攻击”。

参 考 文 献

[1] 张方国，陈晓峰. 基于身份的密码体制综述[R]. 中国密码学会组编．中国密码学发展报告. 北京：电子工业出版社，2009, 8:1-31.Zhang Fang-guo and Chen Xiao-feng. An overview on the identities-based cryptosystem[R]. Chinese Association for Cryptologic Research, Report on Chinese Cryptologic researchment. Beijing: Publishing House of Electronics Industry, 2009, 8: 1-31.

[2] Dodis Y, Reyzin L, and Smith A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data[C].Advances in Cryptology-EUROCRYPT 2004, Interlaken,Switzerland, 2004: 523-540.

[3] Burnett A, Duffy A, and Dowling T. A Biometric Identity Based Signature Scheme[Z]. http://eprint.iacr.org/2004/176.pdf.

[4] Sahai A and Waters B. Fuzzy identity-based encryption.Eurocrypt’05, Springer, 2005, LDCS, 3494: 457-473.

[5] Baek J, Susilo W, and Zhou J. New constructions of fuzzy identity-based encryption[C]. ASIACCS’07, Sydney: ACM,2007: 368-370.

[6] 刘晓东, 将亚丽, 李大兴. 两种基于生物特征信息的签名方案[J]. 山东大学学报(理学版), 2007, 42(12): 24-28.Liu Xiao-dong, Jiang Ya-li, and Li Da-xing. Two biometric identities based signature schemes [J]. Journal of Shandong University(Natural Science), 2007, 42(12): 24-28.

[7] 田捷，杨鑫. 生物特征加密技术概述[J]. 中国自动识别技术，2008, (2): 98-102; 2008, (3): 93-97; 2008, (4): 93-98.Tian Ji and Yang Xin. A Servey on Biometric Encryption[J].China Auto-ID, 2008, (2): 98-102; 2008, (3): 93-97; 2008, (4):93-98.

[8] Izabache M and Pointcheval D. New anonymity notion for identity-based encryption. SCN’08, Springer-Verlag, 2008,LNCS 5229: 375-391.

[9] Boneh D and Hanburg M. Generalized identity based and broadcast encryption schemes. Asiacrypt 2008, LNCS 5350:455-470.

[10] Jiang Wei-qiang, Huang Zheng-quan, and Yang Yi-xian, et al..ID-based authentication scheme combined with identitybased encryption with fingerprint hashing[J]. The Journal of China Posts and Telecommunications, 2008, 15(4): 75-80.

[11] 周亮，李大鹏，杨义先. 基于身份的无需可信任PKG的签名方案[J]. 通信学报，2008, 29(6): 8-12.Zhou Liang, Li Da-peng, and Yang Yi-xian. ID-based signature without trusted PKG[J]. Journal of Communications, 2008, 29(6): 8-12.

[12] 赵学锋，辛小龙. n-挠群上基于多重生物特征身份的签名方案[J]. 计算机工程，2009, 35(14): 148-150.

[13] Cha J and Cheon J. An identity-based signature from Gap Diffie-Hellman groups. PKC 2003, Berlin: Springer-Verlag,2003, LNCS 2567: 18-30.