顺轨干涉SAR浅海地形成像建模及其最优雷达观测参数分析

于祥祯 种劲松 洪 文

①(中国科学院电子学研究所微波成像技术国家级重点实验室 北京 100190)②(中国科学院研究生院 北京 100049)

1 引言

顺轨干涉SAR(Along-Track Interferometric SAR，ATI-SAR)是1987年由美国Goldstein和Zebker[1]首先提出来的一种技术，它通过沿平台运动方向上放置的两个天线对同一场景成像，利用两幅图像间的相位差来获得场景内运动目标的速度信息。当潮流经过浅海地形起伏的区域时，其表面速度会发生改变，这种改变会在顺轨干涉SAR相位图像上有所反映，所以顺轨干涉SAR相位图像可以用来探测浅海地形的变化。同传统SAR一样，顺轨干涉SAR仍然是间接对浅海地形进行成像，但是水深与表面流场的关系比水深与后向散射系数间的关系要明确的多，这就使得顺轨干涉SAR比传统SAR在浅海地形探测方面更具优势。国外前期研究结果也表明，基于顺轨干涉SAR相位图像反演得到的地形精度要比基于传统SAR强度图像获得的精度要高[2,3]。

国外从上世纪90年代就已经开展了顺轨干涉SAR浅海地形探测方面的研究工作。1994年，加拿大遥感中心在Fundy海湾进行了机载顺轨干涉SAR浅海地形探测的飞行试验[4]。1999年到2001年，德国Hamburg大学和GmbH航空雷达遥感研究公司联合开展的EURoPAK-B项目也专门对机载顺轨干涉SAR浅海地形反演等方面进行了研究[2]。目前，国外的研究工作主要是以实测数据的现象分析为主，未从仿真角度对顺轨干涉SAR浅海地形成像进行探讨。由于海洋环境的复杂性、海底地形的多变性，通过实地试验无法对所有情况进行分析。仿真建模是解决这一问题的一种有效手段。通过改变模型参数，可以分析不同条件对成像的影响。

本文根据顺轨干涉SAR对浅海地形成像的机理，并基于浅海海流动力模型、波流交互模型、后向散射模型以及Doppler谱模型对顺轨干涉SAR浅海地形成像进行了仿真建模。通过建立的仿真模型，对不同雷达频率、入射角、顺轨基线长度和极化方式条件下顺轨干涉SAR对浅海地形的成像能力进行了仿真分析，确立对浅海地形观测的最优雷达参数。

2 顺轨干涉SAR浅海地形成像仿真模型

SAR工作在微波波段，其穿透海水的深度仅为毫米到厘米量级，因此顺轨干涉SAR并不能直接观测到水下地形。顺轨干涉SAR对浅海地形的成像机理主要包括以下两个物理过程：(1)水下地形的变化使得流经地形的表面流场速度发生了改变；(2)速度的改变引起顺轨干涉相位的变化，从而使得顺轨干涉SAR相位图像包含水下地形信息。所以顺轨干涉SAR对浅海地形的成像实际上是通过对浅海地形调制后的表面流场进行成像而间接实现的。

根据顺轨干涉SAR浅海地形成像的上述机理，建立顺轨干涉SAR浅海地形成像仿真模型：首先通过浅海海流动力模型进行计算浅海地形调制后的表面流场，然后根据表面流场和输入的风场数据，利用波流交互模型计算空间变化的海浪谱，再通过后向散射模型将空间变化的海浪谱映射成归一化后向散射系数，最后通过Doppler谱模型计算后向散射场每个像元的自相关函数，利用自相关函数与干涉相位的关系得到顺轨干涉SAR的相位差。图1给出了顺轨干涉SAR对浅海地形成像的仿真流程。

图1 顺轨干涉SAR对浅海地形成像的仿真流程

2.1 浅海海流动力模型

表面流场与水下地形之间的关系可以利用各种海洋模式揭示，目前应用比较多的是浅海海流动力模型[5−7]，其具体表达式为

其中u，v分别为x，y方向的速度分量；f为科氏参数；ζ为瞬时水位；h为水深；Cb为底摩擦系数。

利用浅海海流动力模型计算得到的流速为水深平均流速，而顺轨干涉SAR测量的是海表面流速。通常情况下，海表面流速要比平均流速大。考虑到浅海区域水深并不深(＜30 m)，此时表面流速比平均流速大约1%，这样，在计算时可以利用平均流速代替表面流速[7]。

2.2 波流交互模型

水下地形引起的表面流变化的时空尺度小于表面短波的时空尺度，表面流与表面短波相互作用可用弱流体动力作用理论来解释。根据该理论，缓慢变化流场中定常短波谱能量密度的改变可以通过作用平衡方程来描述[8,9]：

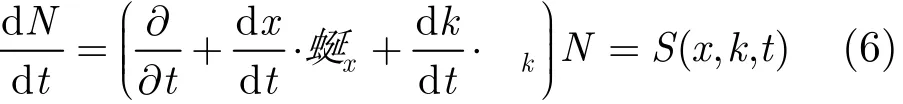
其中N是波包的作用谱密度；x为空间位置矢量；k为波数矢量；S为源函数，是风场输入作用、非线性波-波作用和弥散作用之和，在本文模型中采用的源函数表达式为

其中μ为松弛率，N0为不存在海流时稳定情况下的作用谱密度。

式(6)的求解可以通过沿着相位空间波传播轨道的光路方程来完成，光路方程如下：其中cg(k)为被调制波浪的群速度，U(x, t)为输入的表面流场。

将式(7)，式(8)代入式(6)中，可得

令Q(x, k, t)=1/N(x, k, t)，Q0=1/N0，则式(9)可以转换为

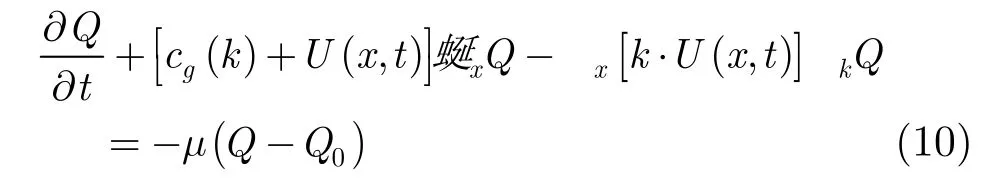
将Q和U(x, t)在空间和时间上进行傅里叶展开，得

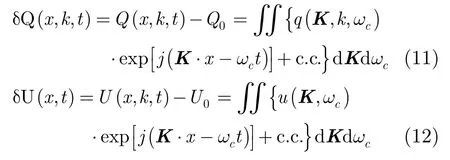
其中c.c.表示共轭，δQ和δU分别表示调制引起的作用谱密度倒数和表面流场的变化量，ωc的积分限为[0,∞)，K的积分区间为整个波谱空间。

假设作用谱密度函数在波数域缓变，则可以认为蜒k。将式(11)和式(12)代入式(10)，化简可得

最后可得空间域的流体动力调制作用表达式为

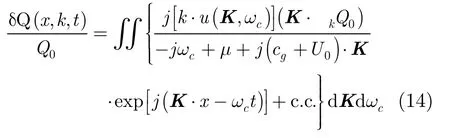
根据作用谱密度与海浪谱的关系：

根据式(14)和式(16)，就可以计算被流场调制后的海浪谱ψ。

2.3 后向散射模型

归一化后向散射系数的计算主要基于Romeiser等提出的改进组合表面模型[10]。该模型以Bragg散射理论为基础，将散射截面基于表面坡度进行2维Taylor展开，考虑了2阶Bragg散射的影响。

根据文献[10]，当海面存在轻微倾斜时，雷达后向散射截面为

其中ke为雷达波数，α为入射角，H为平台高度，b为极化因子，ζ为瞬时海面高度；s=(sp,sn)为平行于和垂直于雷达视向的海面坡度；αl=arccos[cos(α−sp)cossn]为本地入射角；kB=2ke为本地Bragg波波数。

根据改进组合表面模型，综合考虑2阶Bragg散射后的海面归一化后向散射系数为[10]

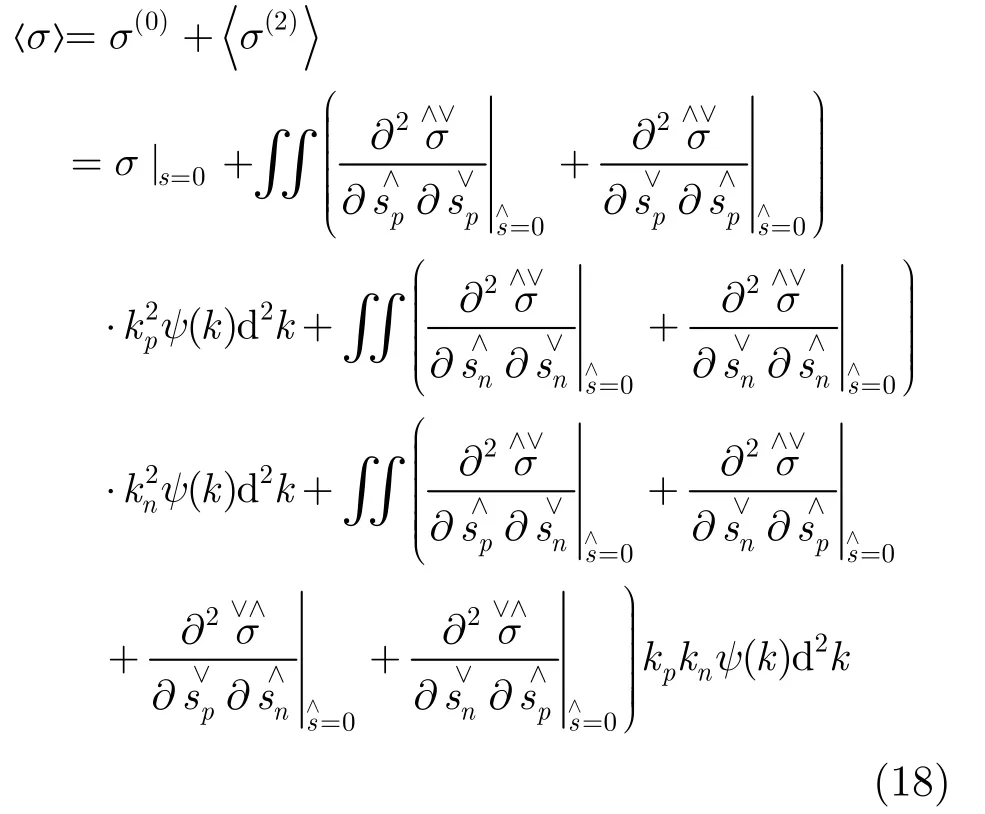
2.4 Doppler谱模型

通常情况下，SAR单视复数据中单个像元的相位并不包含有用信息，因为它是像元内许多单个小散射体散射的相干相位，具有随机分布的特征[11]。但是在一个有限的时间间隔(低于海面去相干时间)，以其中一个天线的信号为参考，后向散射信号的相位变化具有确定性，顺轨干涉SAR就是利用这一原理进行Doppler频移测量。文献[11]指出两幅顺轨干涉SAR图像间的相位差可以用时间间隔τ内后向散射场的自相关函数R(τ)的相位来表示，即其中fD为Doppler频率，S(fD)为Doppler频谱。

因此，为了计算顺轨干涉相位，首先要构造雷达图像每一个像元的Doppler谱，然后计算相应的R(τ)的相位。本文模型中采用基于组合表面模型的Doppler谱计算方法[11]，其表达式为

其中符号±表示远离雷达方向和朝向雷达方向的两组Bragg波分量；表示经过归一化后向散射系数σ加权的平均Doppler频率；γD±表示Doppler谱的方差。和γD±的具体计算过程可以参考文献[11]，这里不再赘述。

3 仿真实验及分析

3.1 水下地形实验设置

水下地形形状采用我国浅海海区较为常见的锯齿状沙波，如图2所示。沙波最高处水深h1=10 m ，总水深h=20 m 。仿真时海区潮流流向为x方向，初始流速u=0.5 m/s 。

3.2 实验结果及分析

根据图1所示的仿真流程，计算了不同雷达频率、入射角、顺轨基线长度和极化方式条件下的顺轨干涉相位：

(1)不同雷达频率对成像的影响 图3给出了P(0.45 GHz)，L(1.3 GHz)，S(3 GHz)，C(5 GHz)，X(9.6 GHz)和Ku(15 GHz)6个不同频率条件下的干涉相位仿真结果。为了方便对比不同波段的干涉相位的变化范围，图3(b)采用相对干涉相位，即Δϕ(n)=ϕ(n)−ϕ(1)。仿真时其他参数分别为：平台高度a=5800 m ，平台速度V=150 m/s ，入射角α=50o，有效基线长度B=0.6 m ，风速4 m/s，风向沿x轴方向。

从图3可以看出：(a)所有频率条件下，干涉相位绝对值大小都随着水下地形高度增加而增大，在水下沙波顶处达到最大值；(b)干涉相位的绝对值与频率成正比，在地形的每一点处，|ϕKu|＞|ϕX|＞|ϕC|＞|ϕS|＞|ϕL|＞|ϕP|；(c)干涉相位的变化范围也与频率成正比，Ku波段的变化范围最大，P波段的变化范围最小。

综上，频率越高越有利于顺轨干涉SAR对水下地形进行成像。

(2)不同入射角对成像的影响 图4给出了不同入射角条件下的干涉相位仿真结果。其中图4(a)给出了绝对干涉相位与入射角的关系，图4(b)给出了相对干涉相位与入射角的关系。仿真时其他参数分别为：平台高度a=5800 m ，平台速度V=150 m/s，频率f=9.6 GHz (X波段)，有效基线长度B=0.6 m ，VV极化，仿真时风速4 m/s，风向沿x轴方向。

从图4可以看出，低入射角情况下(20°)，干涉相位与浅海地形的相关性较差，30°-70°比较适合浅海地形成像；入射角越大，干涉相位差越大(图4(a))，干涉相位变化范围也越大(图4(b))，越有利于顺轨干涉SAR浅海地形成像。

(3)不同基线长度对成像的影响 图5给出了4种不同顺轨基线长度(有效基线长度分别为0.3 m，0.6 m，0.9 m，1.2 m)条件下的绝对干涉相位(图5(a))和相对干涉相位(图5(b))的仿真结果。仿真时其他参数分别为：平台高度a=5800 m ，平台速度V=150 m/s，频率f=9.6 GHz (X波段)，入射角α=50o，VV极化，仿真时风速4 m/s，风向沿x轴方向。

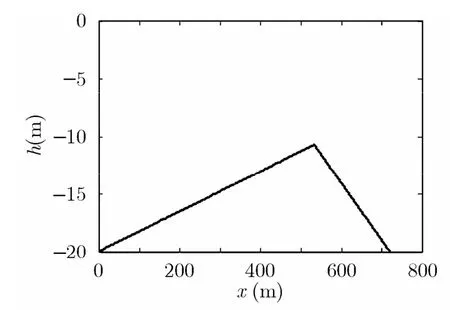
图2 水下地形示意图

图3 顺轨干涉相位与雷达频率的关系

从图5中可以看出，干涉相位与顺轨基线长度成正比(见图5(a))，而且干涉相位的变化范围也与顺轨基线长度成正比(见图5(b))，所以在保证两个天线成像延时低于海面去相关时间的条件下，顺轨基线长度越长越有利于对水下地形进行成像。

(4)不同极化对成像的影响 图6给出了不同极化条件下对水下地形成像的干涉相位仿真结果，其中图6(a)给出了绝对干涉相位与极化的关系，图6(b)给出了相对干涉相位与极化的关系。仿真时其他参数分别为：平台高度a=5800 m ，平台速度V=150 m/s，频率f=9.6 GHz (X波段)，入射角α=50o，有效基线长度B=0.6 m ，风速4 m/s，风向沿x轴方向。

从图6(a)中可以看出，HH极化的干涉相位差的绝对值略大于VV和VH，这种差异随着水下地形高度增加而逐渐减少，而VV和VH极化的干涉相位差的差异不大；从图6(b)可以看出，在水下地形相同的情况下，VV和VH极化干涉相位的变化范围基本相同，都略大于HH。但是从总体上来讲，不同极化方式条件下的干涉相位基本相同，可以认为顺轨干涉SAR对水下地形探测能力与极化方式关系不大。但是由于VV极化方式的海面后向散射最强，信噪比最好[11]，所以VV极化应是顺轨干涉SAR对水下地形探测的首选极化方式。

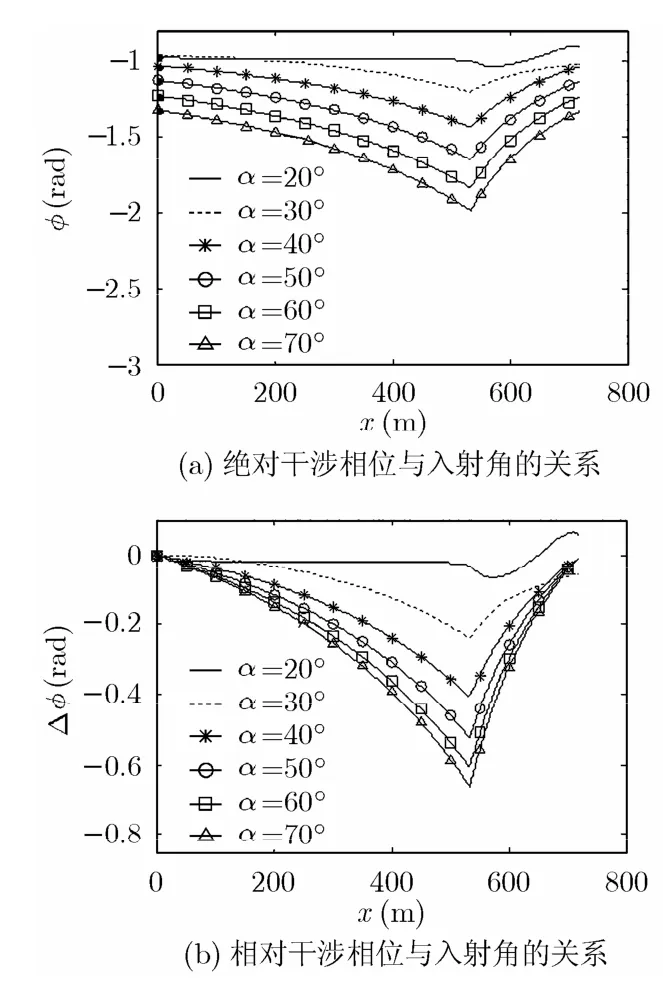
图4 顺轨干涉相位与入射角的关系

图5 顺轨干涉相位与基线长度的关系

图6 顺轨干涉相位与极化方式的关系

4 结束语

本文根据顺轨干涉SAR对浅海地形成像的原理，建立了顺轨干涉SAR浅海地形成像的仿真模型，并探讨了在准1维近似的条件下顺轨干涉SAR对浅海地形成像能力与雷达频率、入射角、基线长度以及极化方式等参数的关系。仿真结果表明：高频率、大入射角以及长顺轨基线条件比较适合于顺轨干涉SAR浅海地形成像；而极化方式对顺轨干涉SAR浅海地形探测能力的影响不大，如果综合考虑信噪比等因素的影响，VV极化仍是顺轨干涉SAR浅海地形成像的首选极化方式。在对浅海海流动力模型进行求解过程中，本文采用了准1维近似的假设，大大简化了数值计算的过程，这对于分析1维走向的地形是足够的，而且也不影响最优雷达参数的分析。但是在实际海洋中，海底地形的变化除了会引起表面速度大小的变化外，还会产生绕流和折射等方向的变化，在进行2维浅海地形干涉相位图像仿真时这些都需要认真考虑，这也是我们下一步需要解决的问题。

[1] Goldstein R M and Zebker H A. Interferometric radar measurement of ocean surface currents[J]. Nature. 1987, 328:707-709.

[2] Romeiser R, Hirsch O, and Gade M. Remote sensing of surface currents and bathymetric features in the German Bight by along-track SAR interferometry[C]. 2000 IEEE International Geoscience and Remote Sensing Symposium(IGARSS’2000), Hawaii, Jul. 24-28, 2000: 1081-1083.

[3] Romeiser R and Runge H. Current in European Coastal Waters and Rivers by Along-Track InSAR. In: Remote Sensing of the European Seas[M]. Springer, the Netherlands,2008: 411-422.

[4] Campbell J W M, Gray A L, and Mattar K E, et al.. Ocean surface feature detection with the CCRS along-track InSAR[J]. Canadian Journal of Remote Sensing. 1997, 23(1):24-37.

[5] 范开国, 黄韦艮, 贺明霞等. SAR浅海水下地形遥感研究进展[J]. 遥感技术与应用. 2008, 23(4): 479-485.Fan K G, Huang W G, and He M X, et al.. Progress on remote sensing of the shallow sea bottom topography by SAR[J].Remote Sensing of Technology and Application, 2008, 23(4):479-485.

[6] 范开国, 傅斌, 黄韦艮等. 浅海水下地形的SAR遥感仿真研究[J]. 海洋学研究, 2009, 27(2): 79-83.Fan K G, Fu B, and Huang W G, et al.. Simulation study on SAR shallow water bathymetry[J]. Journal of Marine Sciences, 2009, 27(2): 79-83.

[7] 傅斌. SAR浅海水下地形探测[D]. [博士论文], 中国海洋大学,2005.Fu B. Shallow sea bottom topography mapping by SAR[D].[Ph.D. dissertation], Ocean University of China, 2005.

[8] Romeiser R and Alpers W. An improved composite surface model for the radar backscattering cross section of the ocean surface 2. Model response to surface roughness variations and the radar imaging of underwater bottom topography[J].Journal of Geophysical Research, 1997, 102(C11):25251-25267.

[9] 余颖, 王小青, 朱敏慧等. 基于二阶散射的海面三尺度雷达后向散射模型[J]. 电子学报, 2008, 36(9): 1771-1775.Yu Y, Wang X Q, and Zhu M H, et al.. Three-scale radar backscattering model of the ocean surface based on second-order scattering[J]. Acta Electronica Sinica, 2008,36(9): 1771-1775.

[10] Romeiser R and Aplers W. An improved composite surface model for the radar backscattering cross section of the ocean surface 1. Theory of the model and optimization/validation by scatterometer data[J]. Journal of Geophysical Research,1997, 102(C11): 25237-25250.

[11] Romeiser R and Thompson D R. Numerical study on the along-track interferometric radar imaging mechanism of oceanic surface currents[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(1): 446-485.