基于时频特征的低分辨雷达微动多目标分辨方法

黄小红 贺 夏 辛玉林 陈曾平

(国防科技大学ATR国防科技重点实验室 长沙 410073)

1 引言

低分辨雷达具有作用距离远，造价低等特点在弹道导弹预警和防空预警得到广泛应用。由于雷达信号带宽窄，径向分辨率很低，通常用来进行单目标探测和跟踪。如果多个目标位于同一雷达波束内，多目标回波信号叠加在一起，将无法进行分辨。然而，在实际应用场景中，常常面临多个目标组成的目标群，如导弹突防时形成弹头和诱饵组成的目标群，编队飞行的飞机群等。如何利用低分辨雷达对这些群目标进行目标运动分辨——目标个数判定，对于指挥决策具有非常重要的参考意义。

目前，关于低分辨雷达群目标分辨的研究主要集中于对群目标波形特征和多普勒特征的分析上，文献[1]研究了利用波形特征进行群目标个数判别的方法，该类方法需事先进行大量样本训练，不利于快速分辨；文献[2,3]研究了利用多普勒信息进行低分辨雷达群目标分辨的方法，该类方法一般采用多个调频斜率近似相同的线性调频信号模型来描述群目标多普勒频率的变化，再通过dechirp处理将回波信号变换为单频信号的叠加实现目标个数的判定。当目标运动速度恒定时，将群目标的雷达回波可看作是多个不同频率的线性调频信号的叠加是合理的，但对于弹道导弹类复杂运动目标回波，则不能用线性调频模型来近似，因此，该类方法不适合用于弹道导弹群目标的分辨。

利用微动特性进行群目标分辨是目前雷达目标识别研究的热点之一。群目标中各目标的运动可以分解为质心的平移运动和相对质心的微动，微动包含加速运动、正弦振动、自旋、章动、翻滚以及复合运动等多种形式，目标微动表征了目标运动状态的细节，可为目标分类识别提供新的途径[4−9]。基于微多普勒的目标分辨的基础是目标的微多普勒之间存在差异，时频分析则是刻画多普勒差异的一种有效数学工具，通过时频分析可以提取振动、转动和机动等目标回波的时频特征，从而实现目标的分辨。然而现有的大多数时频分布[10]都包含交叉项，交叉项强度有时高于信号自身项强度，使得现有时频变换难以直接应用于多目标分辨。针对这一问题，在分析群目标微多普勒变化规律的基础上，提出了利用自适应chirplet变换进行群目标内目标个数判定方法，该算法先利用自适应chirplet变换拟合得到回波中的主要频率成分，消除交叉项的影响，再根据拟合得到的频率分量进行群目标个数的判定。最后给出了数值仿真结果，验证了算法的有效性。

2 群目标微动多普勒分析

微动是指目标除质心平动以外的振动、转动和加速运动等微小运动。目标微动状态下对电磁波的调制使得目标回波多普勒是时变的，表现在频谱上就是存在频谱旁瓣或展宽。下面介绍几种典型微动目标的微多普勒。

2.1 机动点目标

机动点目标，在径向运动规律为R(t)=R0+V t+at2/2，只考虑加速运动情况，则其微多普0勒为

其中R0为目标到雷达的初始距离，λ为雷达发射信号波长，a为目标加速度，可以看出其多普勒呈线性变化，在雷达信号波长一定的条件下，斜率大小取决于目标加速大小。

2.2 正弦振动点目标

正弦振动点目标运动规律可由振幅L和频率f两个参数来表征，在径向运动规律为R(t)=R0+Lsin2πft，微多普勒为

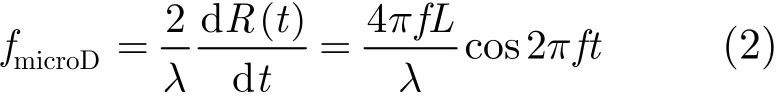
可以看出其多普勒按余弦规律变化，幅度与振幅、振动频率和雷达信号波长有关。

2.3 复合运动点目标

点目标在雷达径向上作加速运动，同时还有半径为L，转速为w的匀速转动，其运动相当于翻滚运动。复合运动点目标，在径向运动规律为

微多普勒为

多普勒沿一直线按余弦规律变化。

2.4 群目标

前面分析了单个点目标微多普勒的变化规律，多目标微多普勒为

假设由多个正弦振动点目标组成，则其微多普勒为

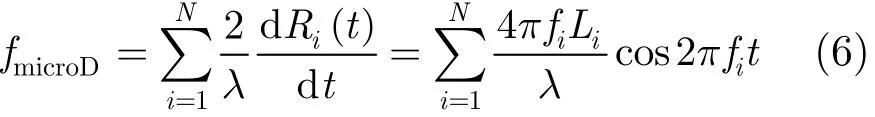
假设由多个机动点目标和多个正弦振动点目标组成，则其微多普勒为

假设由多个复合运动点目标组成，则其微多普勒为

在对目标微多普勒进行分析时可以采用时频分析算法，短时傅里叶变换具有线性特性，但分辨率较低，很少采用。常采用具有较高时频分辨率的WVD及其改进算法，但WVD不是线性的，这类算法对于单目标信号多普勒分析十分有用，应用于多目标信号时会产生交叉项，导致出现虚假频率成分，从而无法正确提取相应的微动特征和判定目标个数。如果能够较好地解决交叉项的干扰问题，则可以实现对多目标微多普勒特征的分析。

3 群目标微动多普勒特征提取

为了分析多目标微多普勒特征，本文提出了利用自适应chirplet变换进行多目标微多普勒分析的方法。该算法根据微动目标多普勒的特点，先对其主要频率成分先进行线性拟合，再利用hough变换[11]对拟合后的线性频率进行处理得到峰值点个数，从而实现群目标个数的判定。

Chirplet变换以chirplet为基函数的线性变换，chirplet是一小段通过窄窗抽取或具有某种包络的线性调频波。由于chirplet基函数集合构成了L2(R)空间的完备集合，根据信号分解原理，就可以将该空间中的任何信号自适应分解到相应的该类基函数上。自适应chirplet分解是以基函数和待分析信号最相似的原则来选择基函数。虽然chirplet基函数不能构成正交基，但可以使用最大投影原理逐步分解，将信号展开成一系列chirplet加权和的形式，即

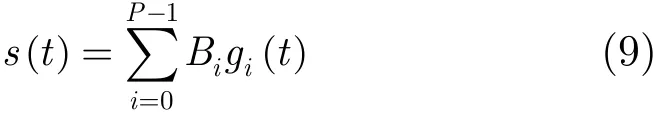
式中σi,ti, fi,βi分别表示chirplet基函数的宽度，时间中心，初始频率和调频率。

基函数按照下列原则进行自适应估计：

其中

si(t)是si−1(t)向基函数gi−1(t)作正交投影后的剩余量。

采用投影匹配算法，以投影能量最大为原则搜索最佳基函数，虽然各个基函数之间不一定正交，但在分解过程中采用的是正交投影，确保了所得到序列的能量类似正交基分解那样简单叠加，因此通过对各chirplet分量WVD叠加得到的信号时频分布重构，不存在交叉项干扰，可以得到较清晰的信号时频分布图。

从式(11)可以看出系数Bi的计算是一个多维非线性优化问题，直接在整个参数空间进行搜索，运算量将非常大，在此可以根据目标回波的特点进行简化。从前面微动目标多普勒分析可以看出，机动点目标微多普勒呈线性变化，正弦振动点目标和复合运动点目标的微多普勒按余弦规律变化，而余弦函数可以用两条直线进行近似拟合，因此可以把微动目标回波信号看作多分量线性调频信号。对于线性调频信号，可以利用信号自身的特点和所包含的参数信息来获得参数的估计[12]。单分量线性调频信号参数估计步骤如下：

(1)计算待分析信号s(t)的Radon-Wigner变换，得到调频斜率的估计值和起始频率。

(2)利用估计值对原信号进行解调频处理，计算解调后信号频率

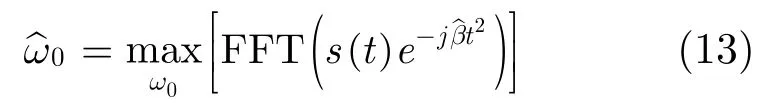
(4)对u(t)计算WV分布，取最大值对应的时刻为s(t)的时间中心估计值。

(7)利用式(11)求系数Bi的估计值。

为了实现对多分量信号，可以将RELAX思想推广到单分量信号估计算法中去，其基本思想是：首先对多分量信号计算Radon-Wigner变换，然后求出强信号的参数，再由上述参数重构此目标信号并从原信号中减去，最后将处理过的信号重复上述处理步骤以估计下一个信号的参数，直到估计出的信号个数等于原信号包含的分量个数。具体步骤如下：

第2步 假设n=2

(c)上述过程反复迭代，直到收敛。

第3步 假设n=3

(c)上述过程反复迭代，直到收敛。

重复上述步骤，直到n=P。算法中每一步的内部收敛判断根据为：比较代价函数在两次迭代过程中的变化值，若此值小于某个预设门限，则认为该过程内部收敛。

4 仿真实验

为了验证算法有效性，对机动点目标和振动目标分别进行仿真。图1为两机动点目标分辨过程图。假设雷达工作频率f0=1 GHz ，PRF=100 Hz ，脉冲积累时间2 s。为了进行对比分析，仿真时将本文方法与文献[2]中的Radon-WVD变换方法进行了对比实验。图1(a)为对回波数据直接做FFT 的结果，从图1(a)中可以看出，由于单目标回波频谱的展宽，两个目标回波的频谱已严重地混叠在一起，无法直接分辨。

图1 两机动点目标回波处理过程

图1(b)为采用Radon-WVD变换求得信号调频斜率，并利用估计结果在时域对回波进行dechirping处理，以减小相干时间内单个目标回波频谱的展宽，最后进行傅里叶变换的结果，从结果图可以看出该方法可以对多目标进行正确分辨。图1(c)为利用自适应chirplet变换进行群目标信号拟合后得到的信号WVD分布图，可以看出交叉项的得到有效消除，只保留了目标主要微动频率分量，由于目标作机动飞行，其频率分量呈线性，利用hough变换检测直线数量，结果图1(d)所示，可见本文方法可以正确分辨目标个数。该实验表明，当目标机动飞行时，由于群目标的雷达回波可看作是多个不同频率的线性调频信号的叠加，本文方法和Radon-WVD变换方法都可以进行群目标分辨。

下面对正弦振动点目标进行仿真。先考虑单个目标情况。假设正弦振动频率f=3 Hz ，幅度L=0.75，回波信号频谱随时间变化如图2(a)所示。对于图2(a)所示的余弦包络，可以用两条直线来近似，如下图2(b)所示。这两条直线的呈对称分布，假设其中一条直线与横轴的夹角为θ，则另一条直线与横轴的夹角为π−θ。用两条直线来进行余弦包络虽然误差较大，由于目标个数判定时不需求精确的多普勒值，所以这种近似拟合是合理。在进行目标检测时，利用这两条直线的对称性，将其判别为一个目标。利用hough变换进行直线检测时需将这两个峰值判定为一个目标，或在进行直线检测前，去掉其中一条对称线。

现在考虑多目标情况，假设f1=2 Hz ，L1=0.45，f2=3 Hz ，L2=0.75。图3(a)为对回波数据直接做FFT 的结果，从图3(a)中可以看出，由于单目标回波频谱的展宽，两个目标回波的频谱已严重地混叠在一起，无法分辨。图3(b)为利用Radon-WVD变换求得信号调频斜率，并利用估计结果在时域对回波进行dechirping 处理，最后进行傅里叶变换的结果，从图可以看出该方法此时不能对多目标进行正确分辨。从图3(c)可以看出由于交叉项的存在，无法从其时频图中分析目标微多普勒变化规律，也无法直接判定目标个数，而且目标回波的WVD分布图没有明显直线特征，与多分量线性调频信号(调频斜率近似相同)的WVD分布图之间存在较大差异，因此不能通过Dechirp处理将回波信号变换为单频信号的叠加来实现目标个数的判定。图3(d)为按本文方法进行处理后的结果，存在3条直线频谱。其中两条直线具有明显对称性，为余弦包络拟合结果，在进行目标检测时，利用这两条直线的对称性，将其判别为一个目标。

5 结束语

低分辨雷达群目标内目标个数判定是低分辨预警雷达目标识别研究的热点，本文对微动群目标微动特性和微多普勒特性进行了分析，根据微动目标微多普勒的特点，提出了利用自适应chirplet变换先进行目标微多普勒拟合分析，再利用分解后目标微多普勒频率呈线性变化的特点，采用hough变换进行直线检测，从而实现了群目标内目标个数的判定。

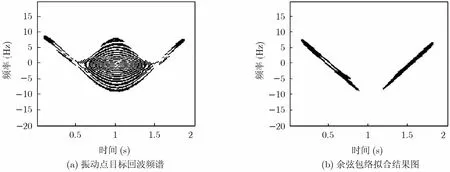
图2 单个正弦振动点目标回波处理过程

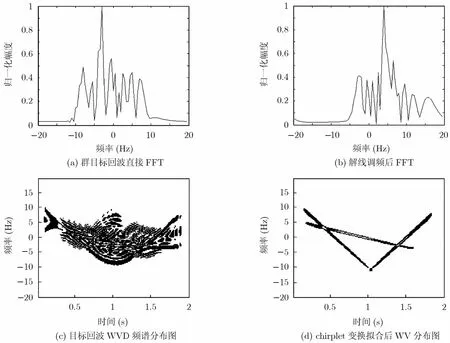
图3 两正弦振动点目标回波处理过程

[1] 王伟, 张汉华, 姜卫东等. 低分辨雷达的目标特征提取方法.国防科技大学学报, 2002, 24(2): 31-35.Wang Wei, Zhang Han-hua, and Jiang Wei-dong, et al.. The study of target feature extracting method based on low-resolution radar. Journal of National University of Defense Technology, 2002, 24(2): 31-35.

[2] 赵学云, 刘峥. 基于Radon-WVD变换的编队目标架次识别.电子与信息学报, 2007, 29(3): 544-548.Zhao Xue-yun and Liu Zheng. Target number detection based on radon-WVD transform. Journal of Electronics &Information Technology, 2007, 29(3): 544-548.

[3] 杜兰, 刘宏伟, 保铮. 一种基于距离-多普勒二维联合的群目标分辨方法. 电子学报, 2004, 32(6): 881-885.Du Lan, Liu Hong-wei, and Bao Zheng. Araid cluster resolution scheme based on join range-doppler processing.Acta Electronica Sinica, 2004, 32(6): 881-885.

[4] Chen V C, Li F Y, and Ho S S. Micro-doppler effect in radarphenomenon, model and simulation study[J]. IEEE Transactions on Aerospace and Electronic System, 2006, 42(1):2-21.

[5] 高红卫, 文树梁. 微多普勒理论建模与仿真研究[J]. 中国电子科学研究院学报, 2008, 3(1): 34-39.Gao Hong-wei and Wen Shu-liang. Micro-Doppler theory modeling and simulating research. Journal of CAEIT, 2008,3(1): 34-39.

[6] 陈行勇, 刘永祥, 黎湘等. 雷达目标微多普勒特征提取. 信号处理, 2007, 23(2): 222-226.Chen Hang-yong, Liu Yong-xiang, and Li Xiang, et al..Extraction of micro-doppler signatures for radar target.Signal Processing, 2007, 23(2): 222-226.

[7] 罗迎, 池龙, 张群等. 用慢时间域积分法实现雷达目标微多普勒信息的提取[J]. 电子与信息学报, 2008, 30(9): 2055-2059.Luo Ying, Chi Long, and Zhang Qun, et al.. Extraction of micro-doppler information based on slow-time integration.Journal of Electronics & Information Technology, 2008, 30(9):2055-2059.

[8] 孙照强, 鲁耀兵, 李宝柱等. 宽带信号及其特征的微多普勒提取技术研究[J]. 系统工程与电子技术, 2008, 30(11):2040-2044.Sun Zhao-qiang, Lu Yao-bing, and Li Bao-zhu, et al..Research on extraction technology of micro-doppler of wideband signal and its properties. Systems Engineering and Electronics, 2008, 30(11): 2040-2044.

[9] 苏婷婷, 孔令讲, 杨建宇. 基于多谐波微多普勒信号分析的目标摄动参数提取方法[J]. 电子与信息学报, 2008, 30(11):2646-2649.Su Ting-ting, Kong Ling-jiang, and Yang Jian-yu. Target parameters extracted from multi-harmonic micro-doppler signal analysis. Journal of Electronics & Information Technology, 2008, 30(11): 2646-2649.

[10] 胡航, 李绍滨, 杨秀萍. 基于高效时频分析的多LFM信号源的DOA估计[J]. 系统工程与电子技术, 2009, 31(3): 534-537.Hu Hang, Li Shao-bin, and Yang Xiu-ping. DOA estimation based on high efficient time-frequency analysis for multiple LFM signal sources. Systems Engineering and Electronics,2009, 31(3): 534-537.

[11] Satzoda R K and Suchitra S. Paralleling the hough transform computation[J]. IEEE signal Processing Letters, 2008, 15:297-300.

[12] 王勇, 姜义成. 基于自适应Chirplet分解的舰船目标ISAR成像[J]. 电子与信息学报, 2006, 28(6): 982-984.Wang Yong and Jiang Yi-cheng. The ISAR imaging of ship based on adaptive chirplet decomposition. Journal of Electronics & Information Technology, 2006, 28(6): 982-984.