正独立映射的判定及其在非凸优化中的应用

张春阳， 张国霜， 李卓识，2， 刘庆怀*

（1.长春工业大学应用数学所，吉林 长春 130012; 2.吉林农业大学信息技术学院，吉林长春 130018）

0 引 言

对于非凸规划，非凸可行域的边界条件在“外法锥条件”或“拟法锥条件”下，文献[1-5]构造了组合同伦内点算法具有大范围收敛性。文献[6]中定义了“正独立映射”，发现了比法锥条件更弱的拟法锥条件，并给出了修正的组合同伦方程。文献[7]给出了弱拟法锥条件定义，并证明在改条件下算法的收敛性。这些条件的发现拓宽了同伦方法求解非凸规划问题的范围。而在判定非凸区域的边界满足什么样的条件时都与正独立映射密切相关，如何判定正独立映射，是实现该算法的重要环节，为此，给出正独立映射的判定方法具有重要意义。

文中将就正独立向量以及正独立映射进行系统的研究，给出其性质及判定方法。

1 正独立向量组与正独立映射

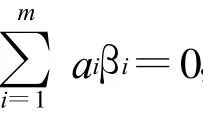
记M={i=1，…，m}在整篇文章中都成立。

定义2 若映射ηi:Rn→Rn，i∈M，在x0∈Rn处满足下边条件:

若

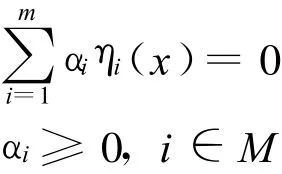
必有

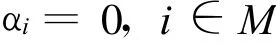
则称η（x）=（η1（x），…，ηm（x））为 x0处的正独立映射。

定义3 若η（x）在D⊂Rn上处处是正独立的，则称η（x）在D上是正独立映射。

命题1 映射η（x）在 x0∈Rn处是正独立映射的充分条件:

（1）当m=n时，rank（η（x0））=n;

（2）当m＜n时，rank（η（x0））=m。

其中

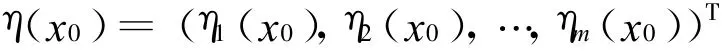
证明:（1）设

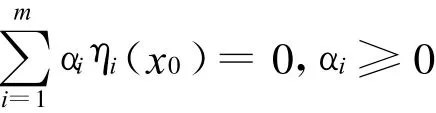
对于

同理可证（2）。

命题2 设向量组βi∈Rn，i∈M，若向量组βi，i∈M是线性独立，则向量组βi，i∈M是正独立的，即

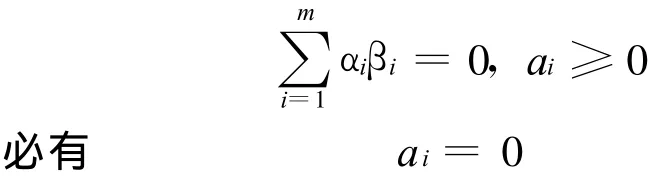
该命题显然成立。

性质:设光滑映射ηi:Rn→Rn，i∈M，任意x∈U（x0）⊂Rn，ηi（x）线性独立，则映射ηi在x0的邻域内是正独立映射。

命题3 设光滑映射ηi:Rn→Rn，i∈M，在x0∈Rn处有ηi（x0）＞0，或ηi（x0）＜0，则ηi在x0处是正独立映射。

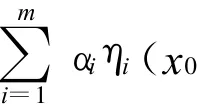
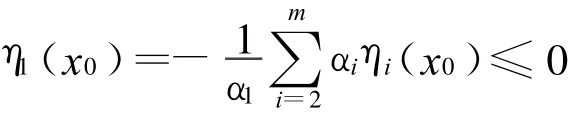
矛盾，命题得证。

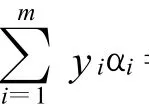
命题4 设向量组βi∈Rn，i∈M，则向量组βi，i∈M是正独立的充分必要条件:存在x∈Rn，使得（β1，β2，…，βm）Tx＜0有解。

证明:

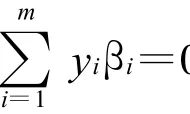
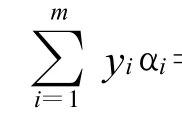
推论 设向量βi∈Rn，i∈M，若βi是正独立向量，则向量组βj也是正独立向量，j=1，…，p，p＜m。

2 非凸优化中的正独立映射的判定

对于优化问题

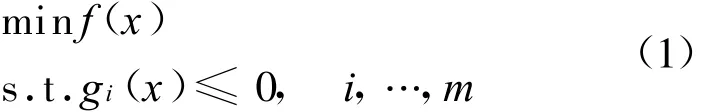
假设f，gi充分光滑。

Ω={x∈R|gi（x）≤0，i=1…，m}表示可行解集;

Ω0={x∈R|gi（x）＜0，i=1…，m}表示严格可行解;

∂Ω=ΩΩ0表示可行解集的边界;

I（x）={i|gi（x）=0，i=1，…，m}表示有效指标集。

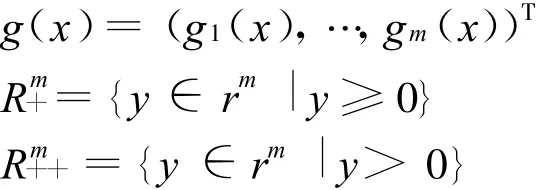
定义4 如果光滑映射η（x）满足对∀x∈∂Ω，若

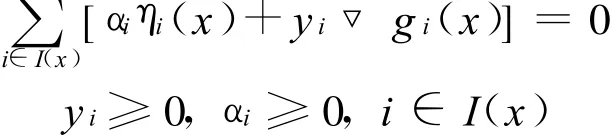
必有

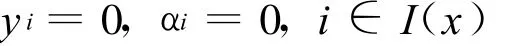
则称η（x）=（η1（x），η2（x），…，ηm（x））T关于▽g（x）正独立。

定理1 映射η（x），关于▽g（x）正独立的充分必要条件是对∀x∈∂Ω，∀t∈（0，1），若

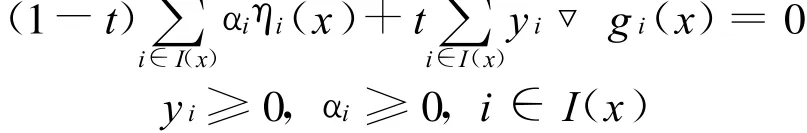
必有

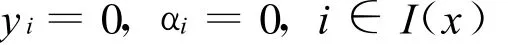
证明:

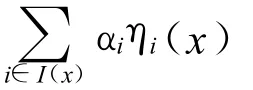
充分条件:用反证法。假设 η（x）关于▽g（x）不是正独立的，即

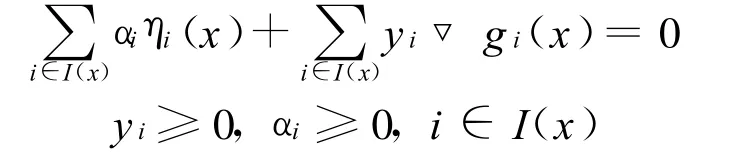
且至少存在 αi1≠0，yi2≠0（若只存在 αi1≠0与η（x）是正独立映射相矛盾，同理不能只有yi2≠0）。不妨设存在 αi1≠0，yi2≠0，再设 αi1=（1-t）β，yi2=tk，其中 β≠0，k≠0则有（1-t）βηi1（x）+tk▽gi2（x）=0。与题设相矛盾。

定理2 设映射ηi:Rn→Rn，i∈M，是连续可微的，若∀x∈∂Ω，对∀i∈I（x），存在1≤j≤n，使得

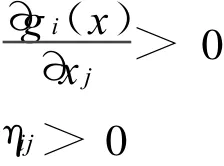
或

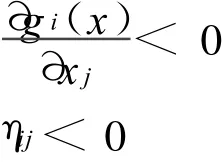
则该映射ηi（x），i∈M，关于▽ g（x）是正独立的，其中

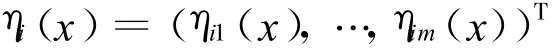
由命题3易证该定理。

定理3 若ηi（x），i∈M，关于▽g（x）是正独立的，则∀x∈∂Ω，有

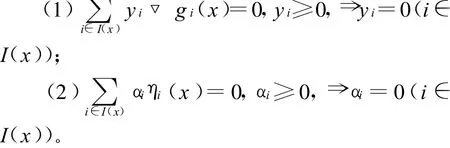
证明:由推论可知定理成立。

定理4 若{ηi（x）|i∈I（x）}是线性独立的，则∀x∈∂Ω，有

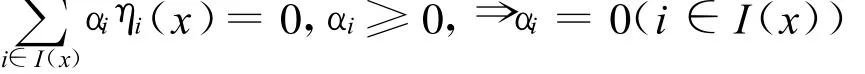
证明:反证法。

定理5 映射ηi（x），i∈M，关于▽g（x）正独立的充分必要条件是∀x∈∂Ω，有:

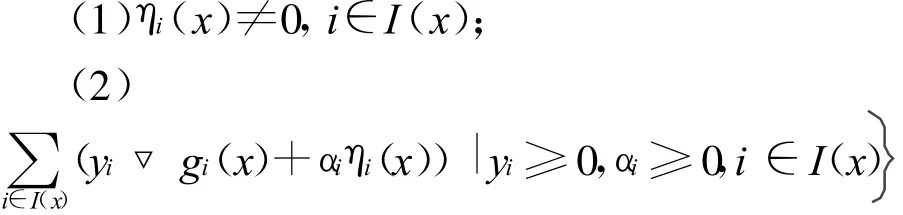
是Rn上的一个尖凸锥。

显然成立。

3 构造方法

例1:Ω={x∈Rn|gi（x）≤0，i=1，2，…，6}，如图1所示。

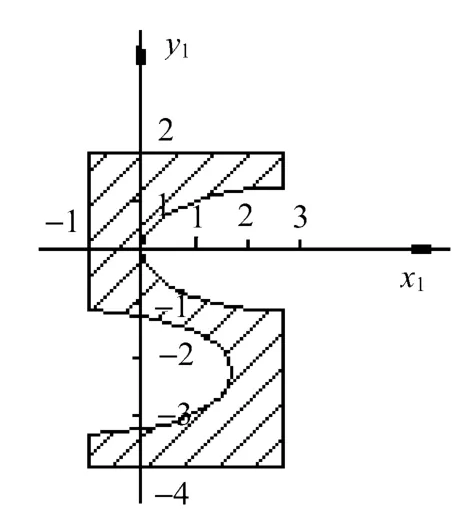
图1 例1可行域

其中约束函数g（x）由下列函数构成:

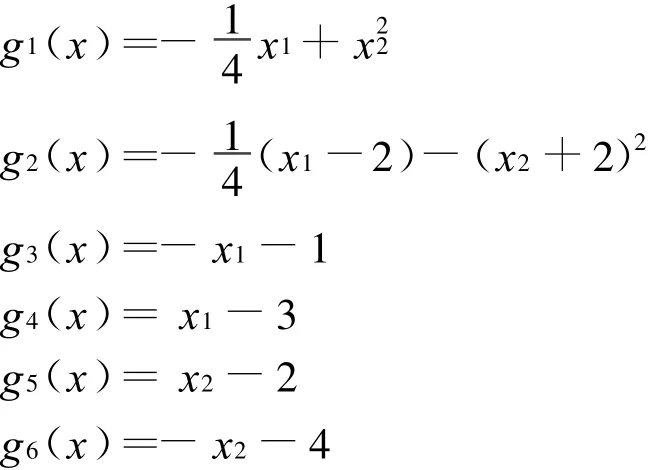
取映射ηi（x）（i=1，2，…，6）如下:

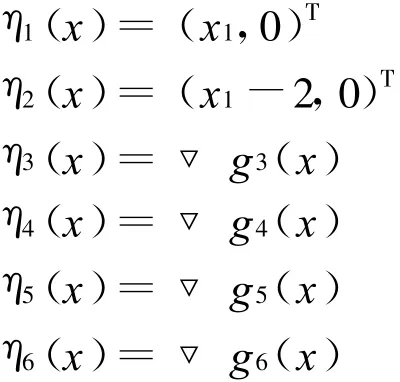
易知ηi（x）是光滑的且关于▽g（x）是正独立的。

例2:Ω={x∈Rn|（g1（x），g2（x））T≤0}，如图2所示。

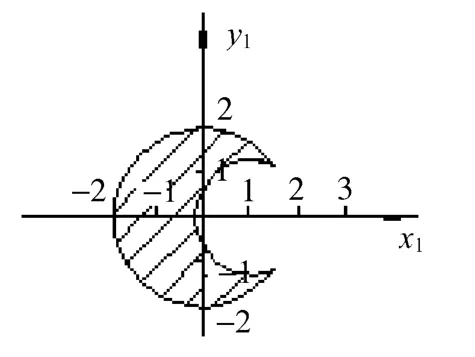
图2 例2可行域

其中约束函数为:

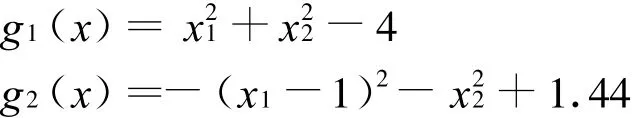
取映射ηi（x）（i=1，2）如下 :

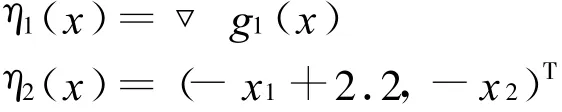
易知ηi（x）是光滑的且关于∂Ω是正独立的。

[1] Feng Guo-chen，Yu Bo.Combined homotopy interior point method for nonlinear programming[J].Problems，Lecture Notes inNum.Anal，1995，14:9-16.

[2] Feng Guo-chen，Lin Zheng-hua，Yu Bo.Existenceof an interior pathway to a Karush-Kuhn-Tucker point of a nonconvex programming problem[J]. Nonlinear Analysis，1998，32:761-768.

[3] Lin Zheng-hua，Yu Bo，Feng Guo-chen.Combined homotopy interior point method forconvex nonlinear programming[J].Appl.Math.Computer，1997，84:193-211.

[4] Yu Bo，Lin Zheng-hua.Homotopy method for a class of nonconvex brouwer fixed pointproblems [J].Appl.Math.Computer，1996，74:65-77.

[5] 林正华，宋岱才，赵立芹.连续求解一般非凸规划的K-K-T点[J].高校应用数学学报，2002，17:207-218.

[6] Liu Qing-huai，Yu Bo，Feng Guo-chen.An interior point path-following mehod for nonconvex programming with quasi normal cone congdition[J].Advances in M athematics of Comunication，2000，29: 281-282.

[7] 王彩玲，刘庆怀，商玉凤，等.一类多目标 Lipschitz规划的最优性充分条件[J].长春工业大学学报:自然科学版，2003，24（3）:17-19.

[8] 高 岩.非光滑优化[M].北京:科学出版社，2008.