组合KdV型方程孤立波的轨道稳定性
张卫国, 卜晓双, 卞兰芸
(上海理工大学理学院,上海 200093)
由JB=T′(0)知B=-1,所以,可定义
1 问题的提出
组合KdV方程
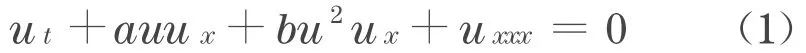
可作为一维非线性晶格传播波的模型[1-3].文献[4]应用约化摄动法于两层流体界面近临界情形也得到了方程(1),因此,方程(1)也是流体力学中的一个重要模型方程.文献[1,5]通过初等积分法求出了方程(1)的渐近值为0的钟状孤波解,文献[6]则得到了这种孤波解的近似解.文献[7]得到了广义组合KdV型方程

的渐近值为零的钟状孤波解.
已有不少文献对KdV型方程的孤波解进行了稳定性研究,例如,文献[8-13]利用变分法研究了KdV型方程
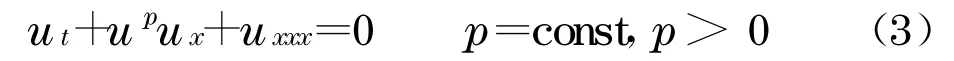
的孤波解的稳定性,得到当0<p<4时方程(3)的孤波解稳定,p>4时不稳定的结论.文献[14]对方程(3)的孤波解给出了当0<p<4时轨道稳定,p≥4时不稳定的结论.文献[15]研究了方程
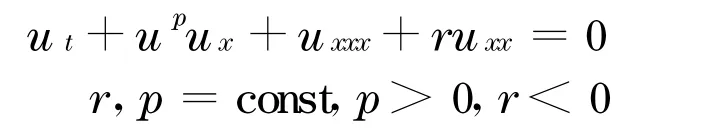
的振荡不稳定性,得到线性不稳定性发生在下列3种情况下:a.波速c固定,且p>4,r足够小;b.r固定,且p>4,波速足够大;c.r固定,且波速c和p都足够大.
文献[16-17]分别利用变分方法和Lyapunov方法研究了方程

的稳定性,给出了使方程(4)的孤波解稳定的充分条件.
容易看出,以往研究KdV型方程孤波解稳定性的文献大多集中于方程中仅含一个非线性项的情形.本文着重研究方程中含有两个非线性项的组合KdV型方程(2)孤立波解的轨道稳定性.关于轨道稳定性的理论参见文献[18-19].由于组合KdV型方程(2)比KdV型方程(3)多一个非线性项bu2pux,它的精确孤波解2002年才被求出[7],所以,以往文献还没有研究过方程(2)的孤波解的轨道稳定性,甚至对作为原型方程的组合KdV方程(1)的孤波解轨道稳定性研究的文献也没有找到.或许有人认为,在其他条件不变的情况下,稳定性主要会受最高次数非线性项的影响.既然KdV型方程(3)的孤波解当0<p<4时轨道稳定,p≥4时不稳定,那么可料想,组合KdV型方程(2)的孤波解相应地可能会在0<p<2时轨道稳定,而在p≥2时不稳定.但事实确并非如此.本文研究的结果表明,组合KdV型方程(2)的孤波解的轨道稳定性不仅受最高次数非线性项bu2pux的影响,还受到另一非线性项aupux的影响.在b>0,0<p≤2情形,得出结论:对于方程(2)的恒正的孤波解u1(x-ct),当a>0时是轨道稳定的,a<0时是轨道不稳定的;对于恒负的孤波解u2 (x-ct),当a<0时是轨道稳定的,a>0时是轨道不稳定的.由此还可知,当p=2,a>0时,组合KdV型方程
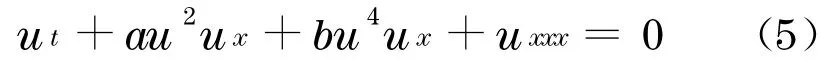
的孤波解是轨道稳定的.方程(5)与p=4时的方程(3)具有相同的最高次非线性项,前者的孤波解轨道稳定,而后者的孤波解轨道不稳定,本文指出了其中的原因,方程(5)中含系数a的这项具有促使稳定化的作用.
为讨论方便起见,现引述文献[7]中的有关结果.
引理1 假设c>0.
a.若b>0或b≥0,且a>0,则方程(2)有钟状孤波解
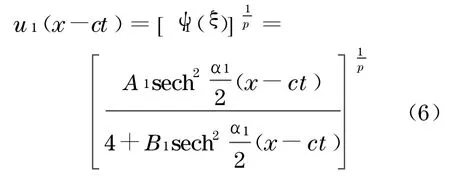
其中
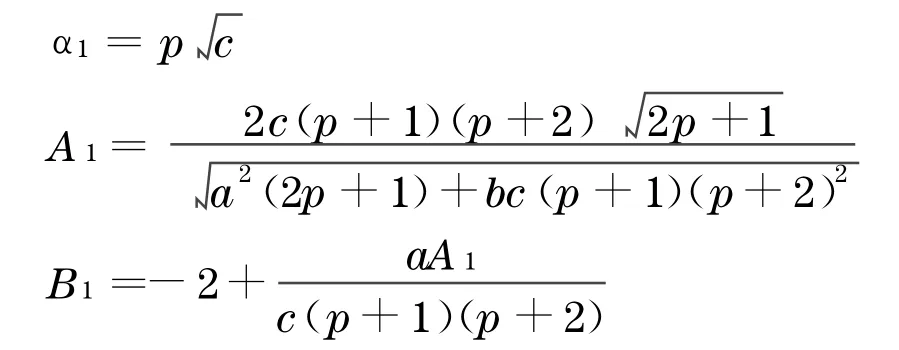

其中

文献[7]已指出,在引理1的a条件下,式(6)中括号内函数ψ1(ξ)恒正,在引理1的b条件下,式(7)中括号内函数ψ2(ξ)恒负.
2 验证方程(2)及其孤波解满足轨道稳定性理论的要求
方程(2)可写成哈密顿系统

其中,X=H2(R),它的对偶空间为X*=H-2(R).
反对称算子

X上的内积为

X与X*间存在自然同构,I∶X→X*,定义为〈If,g〉=(f,g),其中
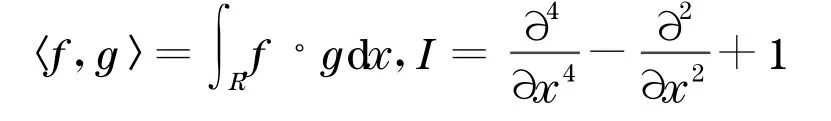
设T是X上具有单参数的酉算子群,定义为T(s)u(◦)=u(◦-s) ∀s∈R,u(◦)∈X(9)显然,
由JB=T′(0)知B=-1,所以,可定义

由式(9)可知,引理1中方程(2)的孤波解式(6)和式(7)可写成T(ct)ui(x)(i=1,2).现考虑孤立波解T(ct)ui(x)的轨道稳定性.为不使重复,取定φc(x)为u1(x)和u2(x)两者之一.验证T(ct) φc(x)满足Grillakis-Shatah-Strauss提出的轨道稳定性理论的要求.
首先,由文献[20]中的定理1和定理2即可推知文献[20]中的系统(3.1)初值问题解的存在性.
引理2[20]设s≥2,对于任意固定的 u0∈Hs(R),方程(2)存在唯一的解u∈C([0,∞); Hs(R)),满足u(0)=u0.
又易证,由式(8)和式(10)定义的E(u),Q(u)分别满足

其次,可证引理3.
引理3 φc是方程(2)的有界态解,且满足
证明 因为φc满足方程(2),代入方程(2)得

对式(11)两边积分可得

因为,当x→∞时,φc,φcx,φcxx→0,所以,C= 0,即

所以
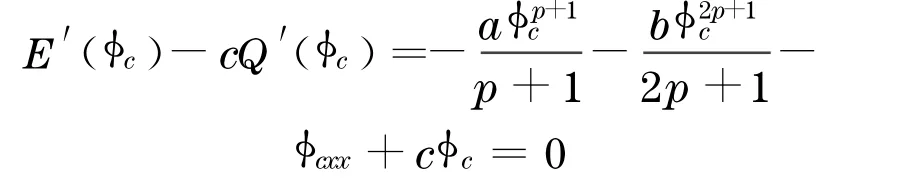
现定义算子Hc:X→X*,Hc=E″(φc)-cQ″(φc),其中

经计算得

易知Hc是一个自共轭算子,Hc=H*c,这意味着I-1Hc为在X上的有界自共轭算子,Hc的特征值由那些使得Hc-λ I不可逆的实数λ组成.
由式(11)可知,λ=0是Hc的一个特征值.
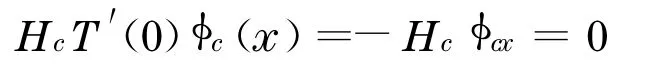
经上述分析可以证明引理4成立.
引理4 对每一个c∈(c1,c2),Hc仅有一个负的简单特征值,且它的核空间由T′(0)φc张成,它的其余的特征植是正的、有界的,而且远离于0.
证明 因为x=0是φcx的唯一零点,由Sturm-Liouville定理知,0是Hc的第二特征值,故Hc只有一个负特征值-σ2,它对应的特征函数 χ满足

于是,可对Hc进行谱分解.令

对∀0≠p∈P,根据文献[18]中的引理可知,对满足(p,χ)=(p,φcx)=0的任意实函数p∈H1(R),存在正数 β>0,使得且β与p无关,则〈Hcp,p〉>0.
因此,空间X可分解为直和X=N+Z+P,其中,Z为Hc的核空间,N是一个有限维空间,P为一个闭子空间.
定义d(c)=E(φc)-cQ(φc),R→R.由于引理2~4成立,据文献[18]可以得到定理1.
定理1 设u1(x-ct),u2(x-ct)是引理1中给定的方程(2)的孤波解,其中,系数p,a,b及波速分别满足引理1中的假设.取定 φc(x)为u1(x)和 u2(x)之一,那么,若 d″(c)>0, T(ct)φc(x)是轨道稳定的;若d″(c)<0,T(ct)φc (x)是轨道不稳定的.
3 组合KdV型方程钟状孤波解的轨道稳定性
为考虑组合KdV型方程钟状孤波解的轨道稳定性,由定理1可知,只需考察d(c)=E(φc)-cQ(φc)二阶导数d″(c)的符号.这里

3.1 b=0时KdV型方程孤波解的轨道稳定性
在引理1的式(6)和式(7)中,令b=0,可得:
a.若a>0,则KdV型方程
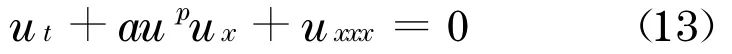
有孤波解

据式(12)有


根据式(16)可得,对于KdV型方程(13)的孤波解式(14),有

故得定理2.
定理2 当0<p<4时,不论a>0或a<0, KdV型方程(13)的孤波解式(14)都是轨道稳定性的;当p>4时,KdV型方程(13)的孤波解式(14)是轨道不稳定性的.
定理2与文献[9-10,14]中的结论相同.从式(17)可清楚地看出,p=4使d″(c)=0,此时,本文所用轨道稳定性判别法失效.
3.2 b≠0的情形
首先考察方程(2)的孤波解式(6)的轨道稳定性判别式d″(c).式(6)可改写为
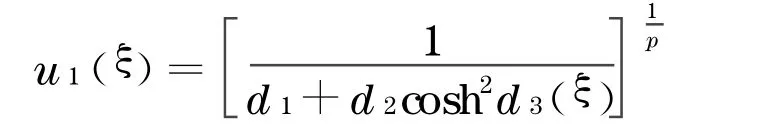
其中,ξ=x-ct.

在式(12)中取φc(x)=u1(x),则有

为讨论d″(c)的正负号,注意式(18)中被积函数关于c的导数,得
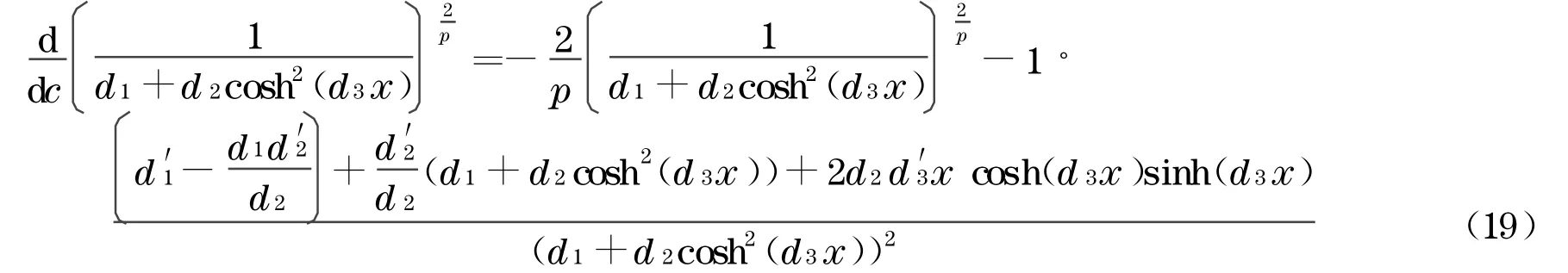
由于d1+d2cosh2(d3x)→∞(当x→∞),当0<p≤2时,是当x→∞时趋于0的有界函数.由式(19)可知,具内闭一致收敛性.故根据含参量积分的求导方法,当0<p≤2时,有

利用分部积分方法可得

再利用积分中值公式,并将式(21)代入式(20),得

其中,x*∈R.

由于

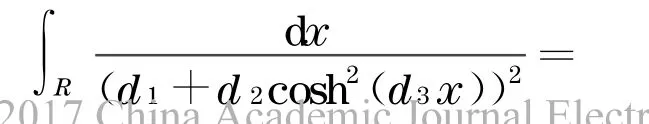

且
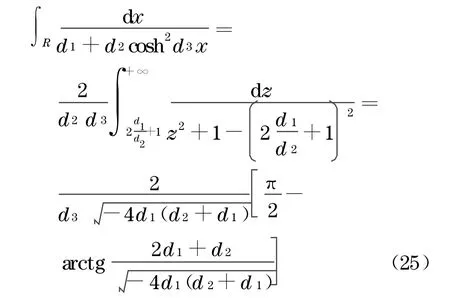
将式(24)和式(25)代入式(23),可得
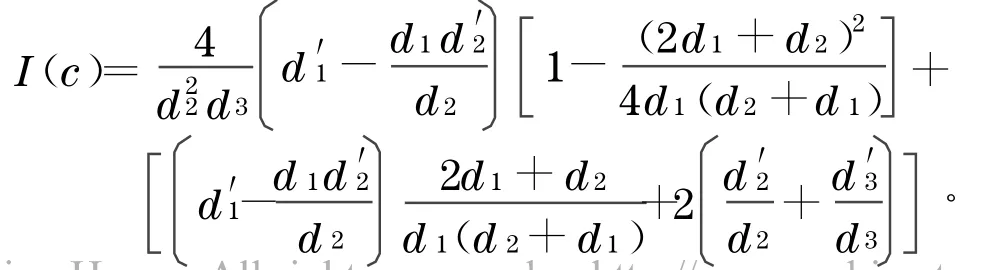

经计算可得
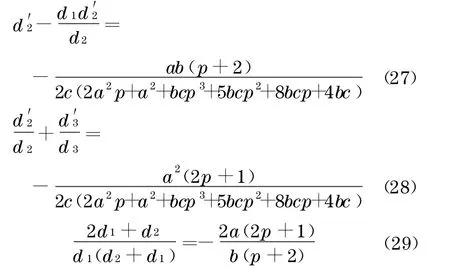
将式(27)~(29)代入式(26),即得

再将式(30)代入式(22),可得关于孤波解u1(x-ct)轨道稳定的判别式
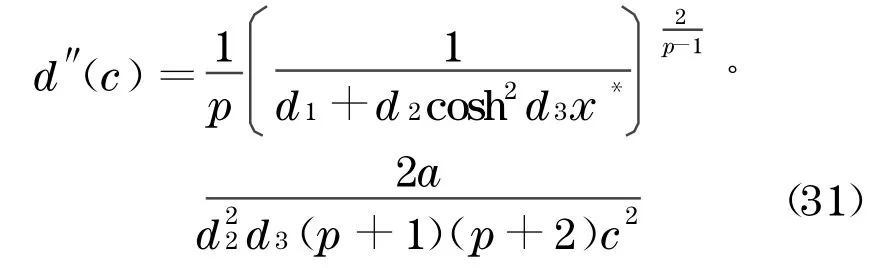
现研究方程(2)的孤波解式(7)的轨道稳定性判别式.



其中
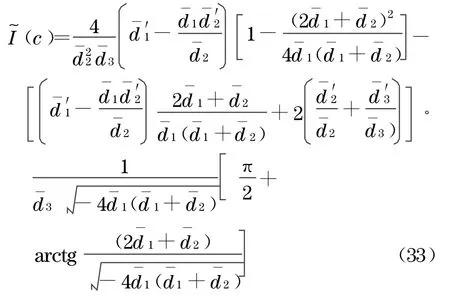

于是,有
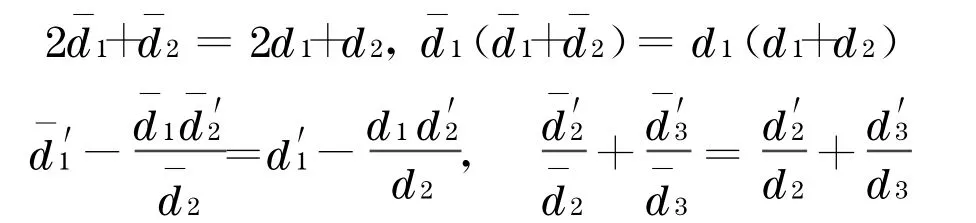
将以上各式代入式(33),得
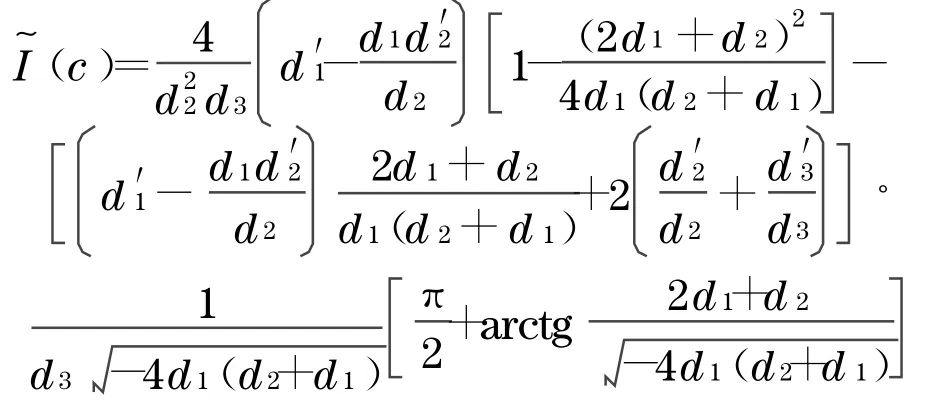
根据式(27)~(30),有

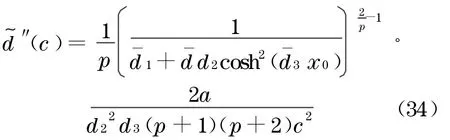
根据式(31)和式(34),且知引理1中关于u1 (x-ct)恒正,而u2(x-ct)的表达式(7)中ψ2(ξ)恒负,可以推出结论:
a.对于u1(x-ct),当a>0时,d″(c)>0,当a<0时,d″(c)<0;
根据以上述结论和定理1,得到定理3.
定理3 设b>0,0<p≤2.
a.组合KdV型方程(2)的孤波解u1(x-ct).当a>0时是轨道稳定的,a<0时是轨道不稳定的;
b.组合KdV型方程(2)的孤波解u2(x-ct).当a<0时是轨道稳定的,a>0时是轨道不稳定的.
根据定理3,在方程(2)中取p=2,可知组合KdV型方程(5)的钟状孤波解当a>0时是轨道稳定的.又根据前面的讨论及文献[14]可知,若在方程(5)中令a=0,则KdV型方程

的钟状孤波解是不稳定的.究其内在原因,考虑式(18),当p=2时,利用式(25)直接可得

由式(35)可知,当a=0时,d′(c)关于c为常数,自然有d″(c)=0;当a≠0时,d′(c)随着a的增加而减少,随着c的增加而增大,所以,方程(5)中含a的这项的出现减弱了不稳定性,起到了某种稳定化的作用.
[1] WADATI M.Wave propagation in nonlinear latticeⅠ[J].J Phys Soc Japan,1975,38(3):673-680.
[2] WADATI M.Wave propagation in nonlinear latticeⅡ[J].J Phys Soc Japan,1975,38(3):681-686.
[3] TODA M.Waves in nonlinear lattice[J].Supp Progr Theo Phys,1970,45:174-200.
[4] 戴世强.两层流体界面上的孤立波[J].应用数学和力学,1982,3(6):721-731.
[5] 潘秀德.组合KdV方程的孤立波解与相似解[J].应用数学和力学,1988,9(3):281-285.
[6] 戴世强.若干强非线性问题的近似解析解[J].中国科学(A辑),1990,33(2):153-162.
[7] ZHANG Weiguo,CHANG Qianshun,JIANG Baoguo. Explicit exact solitary-wave solutions for compound KdV-type and compound KdV-Burgers-type equations with nonlinear terms of any order[J].Chaos,Solitons and Fractals,2002,13(2):311-319.
[8] LAEDKE E W,SJPATSCHEK K H.Stability theorem for KdV equations[J].J Plasma Phys,1984,101(9): 263-272.
[9] BENJIAMIN T B.The stability of solitary weave[J]. Proc R SocLondon,A,1972(328):153-183.
[10] BONA J L.On the stability of solitary waves[J].Proc R Soc London,A,1975(344):363-374.
[11] PEGO R L,WENISTEIN M I.Eigenvalues and solitary wave instabilities[J].Phil Trans R Soc London,A, 1992,340:47-94.
[12] WEINSTEIN M I.Lyapunov stability of ground states of nonlinear dispersive evolution equations[J].Commun Pure Appl Math,1986,39:51-68.
[13] WENISTEIN M I.Existence and dynamic stability of solitary wave solutions equations arising in long wave propagation[J].Commun Partial Differential Equation,1987,12(10):1 133-1 173.
[14] BONA J L,SOUGANIDIS P E,STRUSS W A.Stability and instability of solitary waves of Korteweg-de Vries type[J].Proc R SocLondon,A,1987(411):395-412.
[15] PEGO P L,SMEREKA P,WEINSTEIN M I.Oscillatory instability of traveling waves for a KdV-Burgers eqution[J].Physical D,1993,67(1/2/3):45-65.
[16] KARPMAN V I.Stabilization of soliton instabilities by higher order dispersion:KdV-type equations[J].Phys Lett,A,1996,210(1/2):77-84.
[17] KARPMAN V I.Lyapunov approach to the soliton stability in highly dispersives-systems.Ⅱ.KdV-type equations[J].Phys Lett,A,1996,215(5/6):257-259.
[18] GRILLAKIS M,SHATAH J,STRAUSS W.Stability theory of solitary waves in the presence of symmetryⅠ[J].J Funct Anal,1987,74(1):160-197.
[19] GRILLAKIS M,SHATAH J,STRAUSS W.Stability theory of solitary waves in the presence of symmetryⅡ[J].J Funct Anal,1990,94(2):308-348.
[20] TOSIOK.On the Korteweg-de Vries equation[J]. Manuscripta Math,1979,28(1/2/3):89-99.

