基于PID加校正的导弹纵向回路控制与仿真

江秀强，谭 飞

（四川理工学院 自动化与电子信息学院，四川 自贡 643000）

随着现代战争形势的多样化发展，导弹的目标种类不断增加，使导弹向高精度、高智能、小型化、多用途发展。导弹控制系统的任务就是控制导弹对目标进行快速的精确打击。粗略地看，导弹控制系统都是由控制器和被控对象两大部分组成的。虽然不同型号的导弹，控制系统的具体组成有所区别，构成的回路也不尽一样；但是，既然是依据自动控制原理组成的导弹控制系统，所组成的回路也是有共性的。

高速、大机动、小型化已成为当今导弹目标的重要特征。攻击目标的高速、大机动特性导致弹——目相对运动加剧，对导弹的快速反应能力提出很高要求。攻击目标的小型化特征，又给导弹控制的准确性带来了不小的困难。而目标的高速、大机动、小型化的特征，必然导致弹——目运动轨迹更加复杂，使得导弹所遇到的不确定因素增加，对维持系统稳定性又是一个考验。为了解决这些矛盾，本文采用PID加校正的控制方法控制导弹纵向回路，对PID控制参数进行了合理选取、设计了相应的校正装置，并对系统的控制效果进行了仿真分析。

1 控制模型的建立

研究导弹控制问题，必须以一定的数学模型为基础。在选择适当的坐标系后，由导弹纵向回路的动力学模型。分析推导出相应的传递函数，建立控制系统模型。

1.1 动力学方程

导弹纵向动力学方程为：

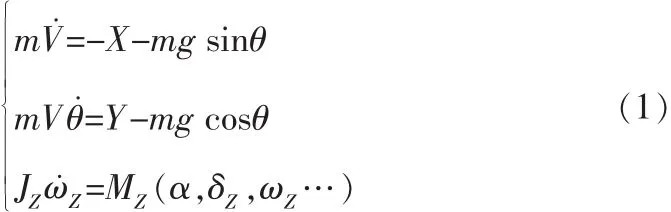
1.2 传递函数

传统的控制方案是将舵机简化为一个比例环节，系统仅存在角速度反馈，其纵向通道传递函数为:

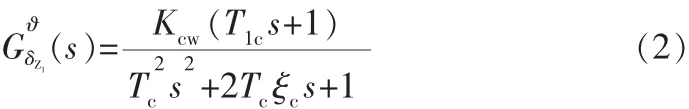
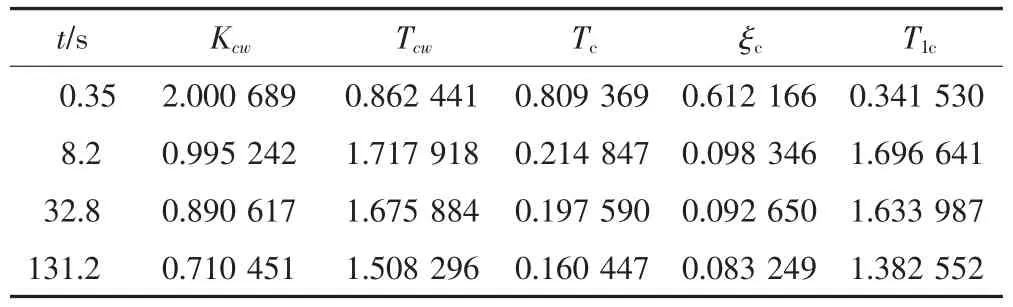
表1 导弹纵向回路传递函数的各参数值Tab.1 Transfer function parameters of missile longitudinal loop

1.3 导弹飞行控制特征点的选取

导弹飞行过程中几个有代表性的状态点，叫做导弹飞行控制的特征点。选取特征点的原则：在被选定的特征点上，导弹的控制系统最难实现导引系统发出的指令、最难满足要求，因此如果所选特征点的控制效果满足要求的话，那么在其他点也是满足的。通常选取助推段和续航段上的4个特征点：0.35、8.2、32.8、131.2 s来研究[2-3]。

1.4 纵向回路控制系统

图1为导弹纵向运动的闭环控制系统结构图。

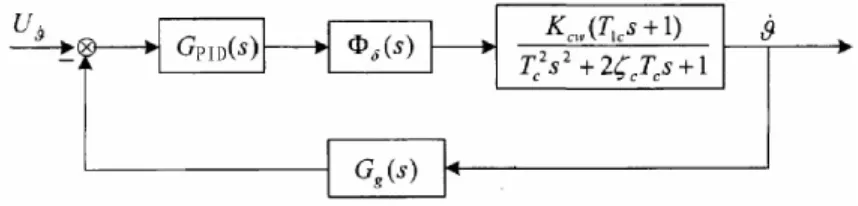
图1 导弹纵向运动的闭环控制系统结构图Fig.1 Closed-loop control system structure of missile longitudinal motion

图 1 中，Φδ（s）为舵系统的闭环传递函数；GPID（s）为 PID控制器的传递函数；Gg（s）为角速度陀螺仪的传递函数；

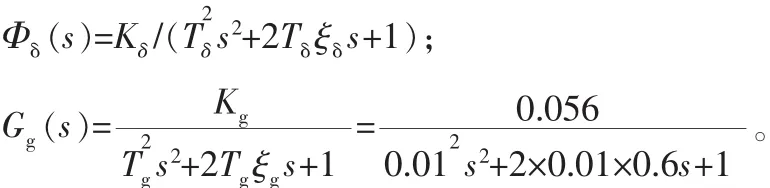
由于舵系统和陀螺仪的时间常数相比弹体环节的时间常数[2]来说都要小得多，所以可以将 Φδ（s）、Gg（s）、Gc1（s）近似为相应的比例环节，即：Φδ（s）≈Kδ=3.6、Gg（s）≈Kg=0.056。

使用PID控制器进行控制，即

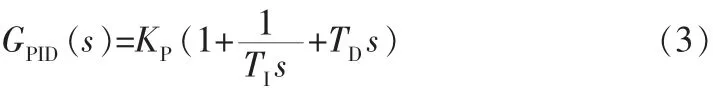
要满足控制系统[4]的设计要求：相角裕度大于30°，幅值裕度大于6 dB。这里TI和TD的设计就应该满足：

这样以来，PID控制器就能提供一个超前相角来抵消弹体环节的滞后相角，从而增大相角裕度，保证相角裕度满足要求。

两点夹持模式下夹持器结构参数的优化结果如表2所示。图3为结构参数优化前后夹持力的对比。可见优化后，在夹持不同尺寸物体时，夹持力平均提升幅度为20.00%。

2 PID加校正控制

2.1 PID控制器的设计

弹体传递函数属于小阻尼振荡环节，幅频特性具有谐振峰值，相频特性下降迅速。依据文献[5]中的方法，为了使PID控制器起到较大的作用，并使参数设计得到简化，进行如下设计：使PID控制器的分子能抵消弹体传递函数与舵回路的闭环传递函数乘积的分母（忽略其高阶项），忽略1）（s2+2Tcξcs+1）的高阶项，得到:

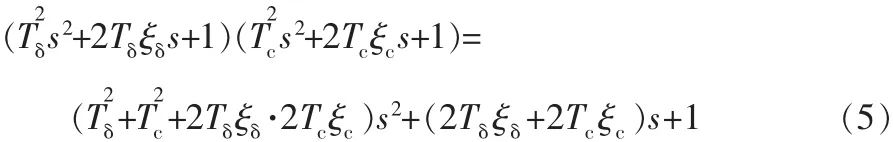
则：

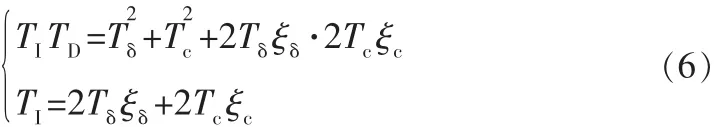
回路的开环传递函数为：

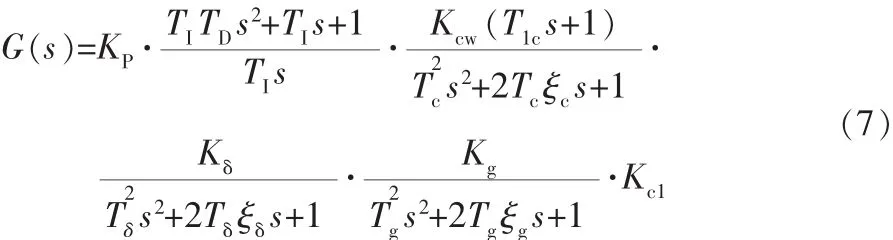
这里使PID控制器的分子抵消弹体、舵回路的分母，可得到：

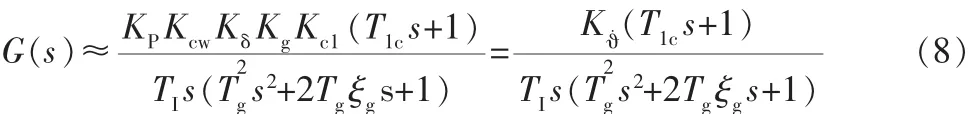
式中，Kϑ˙=KPKcwKδKgKc1。

这样，系统的稳态输出就与弹体的参数无关。

根据幅频特性和相频特性的要求，可以计算出各特征点的PID控制参数，如表2所示。图2和图3分别给出了校正前系统的阶跃响应曲线和Bode图。

表2 各特征点的PID控制参数Tab.2 PID control parameters of each feature points

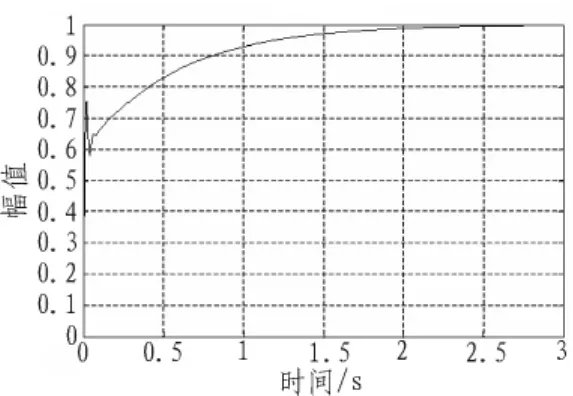
图2 校正前的系统阶跃响应曲线Fig.2 Step response curve of the uncorrected system

由上述仿真可以看出，常规PID对导弹纵向回路的控制效果并不理想，需要设计一种校正装置与控制器串联来加以改善。

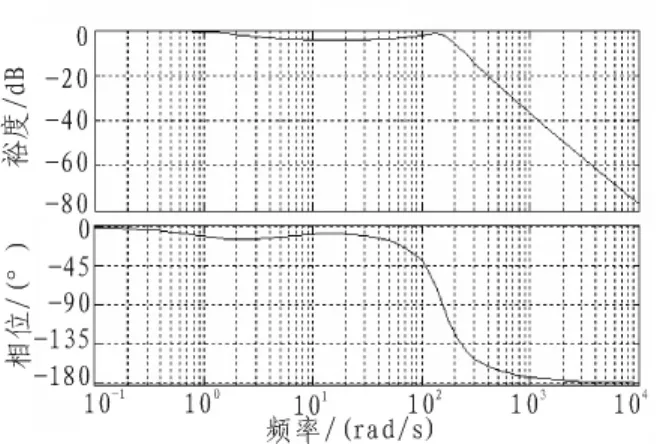
图3 校正前的系统Bode图Fig.3 Bode curve of the uncorrected system

2.2 校正装置的设计

由上文所述导弹动力学的基本参数可以看出：导弹刚点火的0.35 s的各项参数与续航段其他特征点的参数差别较大。所以，在设计校正装置的时，单独设计0.35 s时刻的校正装置，而对其他3个特征点统一设计一个校正装置进行校正。依据文献[6]中的方法，运用MATLAB中的SISO工具进行校正装置的设计，如图4、图5所示，得出第一个特征点的校正环节其他特征点的校正环节

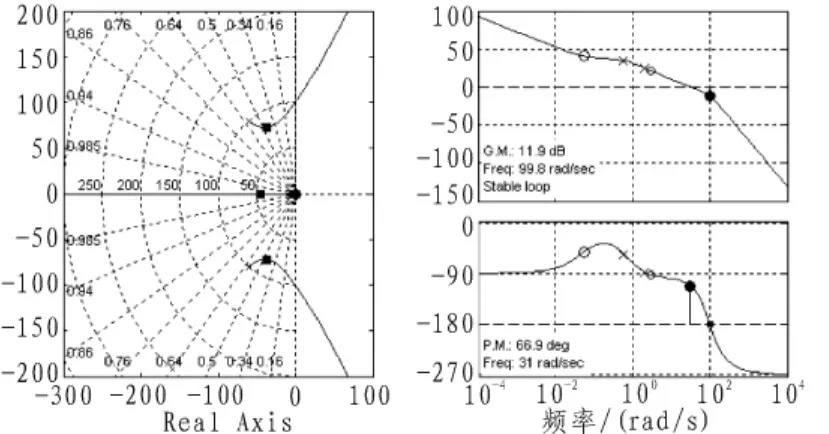
图4 设计0.35 s时的校正装置Fig.4 To design a correction device on 0.35s

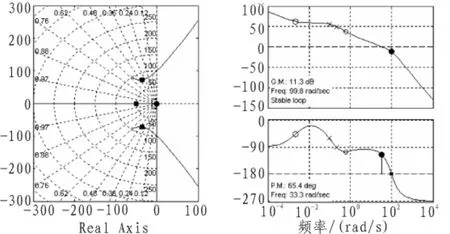
图5 设计8.2、32.8、131.2 s时的校正装置Fig.5 To design correction devices on 8.2s,32.8s,131.2s

由图4、图5可以看出：第一个特征点与其他3个特征点采用2个参数不同的校正装置校正后的系统参数都是满足要求的。其实，2个校正装置都是滞后-超前校正，在实际中易于实现，而且2个校正环节的相互切换也很简便。

由图6与图3相对比，可以看出：校正后系统稳定性具有明显提高，动态性能也得到显著改善。

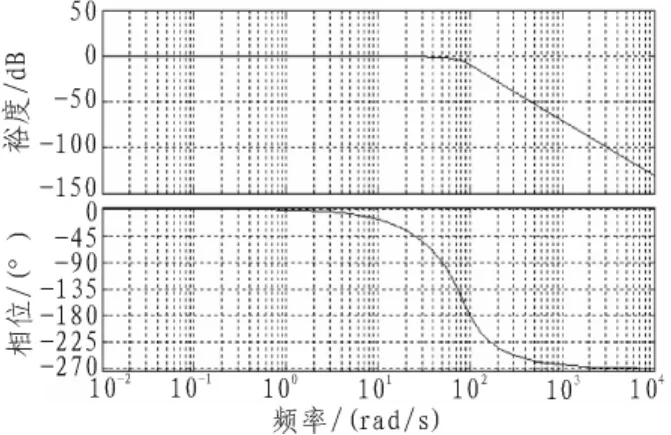
图6 加入校正装置后系统的Bode图Fig.6 Bode curve of the corrected system

3 仿真结果

为了验证控制效果，对系统加入单位阶跃信号进行仿真，并与相关文献对比仿真结果，如图7～图10所示。

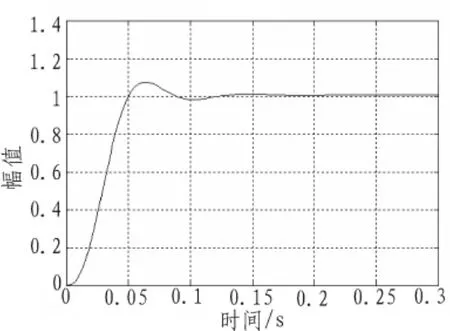
图7 0.35 s时的系统阶跃响应曲线Fig.7 Step response curve of the corrected system on 0.35s

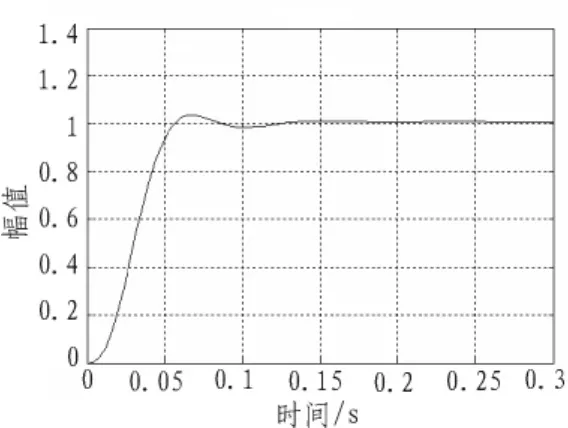
图8 8.2 s时的系统阶跃响应曲线Fig.8 Step response curve of the corrected system on 8.2s

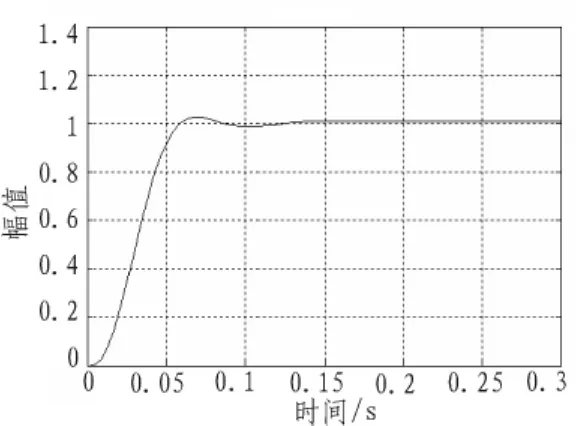
图9 32.8 s时的系统阶跃响应曲线Fig.9 Step response curve of the corrected system on 32.8s

由仿真结果可以看出，PID加校正的控制方法对导弹纵向回路的阶跃响应曲线反应良好。各特征点的超调量分别为7.4%、3.6%、2.5%、1.2%，比文献[1]中 11.4%的超调量明显降低了；各特征点的上升时间分别为 44.97、47.52、48.78、50.69 ms，比文献[1]中170.6 ms的上升时间显著提前了；各特征点的调节时间（2%误差带）分别为 81.75、78.32、75.85、59.93 ms，比文献[1]中356.3 ms的调节时间大大缩短；而稳态误差与文献[1]中相同，仍然为0。

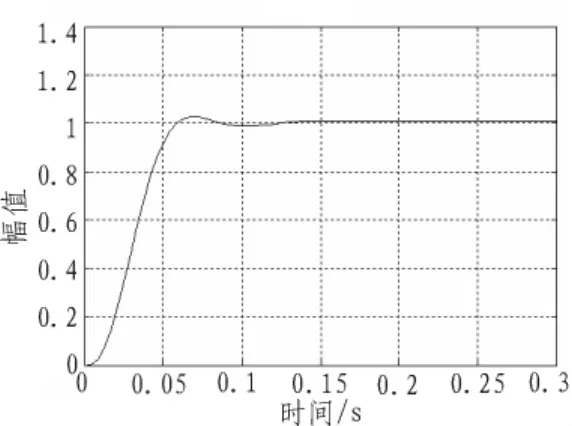
图10 131.2 s时的系统阶跃响应曲线Fig.10 Step response curve of the corrected system on 131.2s

4 结 论

本文先参考相关文献建立了导弹纵向回路控制系统模型，然后利用理论计算的方法设计了PID控制器参数，接着利用MATLAB的SISOTOOL工具设计了相应的校正装置，最后进行了系统仿真。与文献[1]对比仿真结果可以看出，通过合理设计PID控制器的参数并加入适当的校正环节，能够使系统在保证控制准确性的同时，大大提高控制的快速性，增强系统稳定性，是一大改进，且仿真也证明此控制方法具有较强的鲁棒性。利用PID加校正的控制方法可以在文献[1]的基础上进一步提高传统气动力导弹控制系统的性能，更能满足导弹稳定运行、快速反应、精确打击的能力的要求。当然这里只是给出了与文献[1]控制方案相比较的分析结果，实际的参数还需要在实物仿真中不断调试和修正，最终得到令人满意的控制效果，才能运用于实战。

[1] 刘冰，高嵩，何宁，等.基于PID控制的导弹分通道仿真[J].电子设计工程，2009，17（11）:97-99.LIU Bin,GAO Song,HE Ning,et al.Missile sub-channel simulation based on PID control[J].Electronic Design Engineering,2009,17（11）:97-99.

[2] 钱杏芳，林瑞熊，赵亚男.导弹飞行力学[M].北京:北京理工大学出版社，2006.

[3] 李新国，方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社，2005.

[4] 胡寿松.自动控制原理[M].北京:科学出版社，2007.

[5] 刘兴堂.精确制导、控制与仿真技术[M].北京:国防工业出版社，2006:62-72.

[6] 杨涤，耿云海，杨旭 等.飞行器系统仿真与CAD[M].哈尔滨：哈尔滨工业大学出版社，2005:97-102.