对数函数控制下强流离子束径向密度的模拟研究

杨翠云 翁甲强 刘海英

1（桂林师范高等专科学校 物理与信息技术系 桂林 541002）

2（广西师范大学 物理科学与技术学院 桂林 541004）

核能源是世界公认的洁净、绿色、低碳的高效能源，排在替代化石能源的第一位[1]。但是，发展核能源存在天然铀的利用率低、核废料难以处理等难题。二十世纪末提出的加速器驱动的次临界反应堆，即“放射性洁净核能系统”，是解决这一难题的最佳选择[2]。而应用强流离子束还须解决束晕-混沌的控制问题打到器壁上的束晕离子不仅损害设备，且危害人身安全。为控制束晕-混沌，中国原子能研究院方锦清[3]提出非线性控制策略。基于该策略，人们已提出一些有效的控制方法[4–9]。此外，为提高离子束的利用率而进行的离子束束流品质研究(即离子束径向密度)中[10–13]，发现在某些参数下受控后的离子束径向密度的分布变得不均匀，甚至有峰值出现，且分布与控制器和选用的控制信息有关。但是，对束流品质的现有研究中常用的控制变量是离子束的均方根半径 rrms或最大半径 rmax，唯有文献[10]采用的控制变量为离子数比 λ=Na/N (Na为匹配半径外的离子数，N为总离子数，常数)，但对以匹配半径外特定区域(控制信息区域)内的离子数N'a代替Na作为控制变量，尚未见报道。N'a代替Na，可大大缩小探测控制信息的区域，可解决控制变量的探测问题，成为最具有可行性的实施方法[9]。

本文采用 PIC程序和对数函数控制器G=gln(1–λ′) (g 为增益因子，λ′=Na'/N)进行束晕-混沌控制的模拟研究。结果表明，受控后，离子束进入加速器通道的一段时间内，束中心处的密度值变化很大，然后趋于稳定；在整个运动过程，离子束的径向密度保持基本均匀分布，而且，该分布与控制信息的选取区域无关。

1 理论模型和数值模拟方法

粒子-束核模型广泛应用于强流离子束的束晕-混沌形成机制及其控制方法研究[3–17]。该模型考虑一束横截面为圆形的离子束在周期性聚焦磁场B(r,s)通道中运动，对于满足K-V分布(Kapchinsky-Vladimirsky propagation)的离子束，可用包络方程描述离子束包络半径的变化[14–16]，即：

式中，rb是束包络半径；S为聚焦磁场的周期；s=z=βbct是轴向坐标，βbc为束离子的平均轴向速度，c为光速，t是时间；周期函数κz(s)表征周期性聚焦磁场强度(图 1)，满足 κz(s+S)= κz(s)=q2Bz2(s)/(4γb2βb2m2c4)，Bz(s)=Bz(0,s)，q 和 m 分别为离子的电量和静止质量，γb=1/(1–βb2)1/2为相对论因子；ε是离子束发射度；K=2q2Nb/(γb2βb2mc2)是广义导流系数，为束自生场强度的量度，Nb是轴向单位长度上的粒子数目。在该磁场中一个周期内的真空相移o0=[ΓS2κz(0)]1/2，Γ是聚焦磁场的填充因子，表示磁场的大小。

引入无量纲的参数和变量

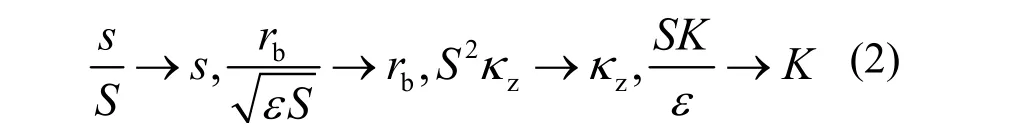
则式(1)可改写为

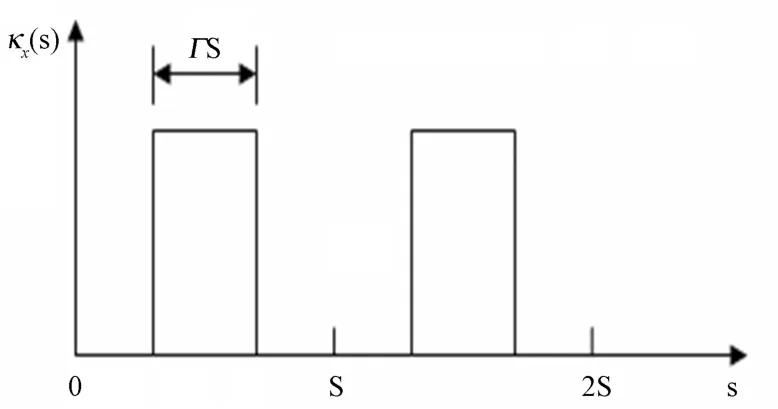
图1 周期性聚焦磁场和填充因子Fig.1 The periodic function and filling factors.

而描述单离子横向运动的方程则分别为

其中 Φs(x,y,s)为空间电荷自生场的势函数，满足Poisson方程[5]

其中f (x,y,x′,y′,s)为在非相对论四维相空间内的横向离子分布函数，ε0为真空介电常数。

在粒子-束核模型里，自生场的非线性效应使粒子和束核不断地发生能量交换，部分粒子获得较大的能量跑到束核外面成为束晕离子。单离子运动时受到的力有自生场力 Fsc=–q▽Φs(x,y,s)和外加聚焦磁场力Fext=κz(s)，即

根据文献[3]提出的非线性控制策略，将非线性控制器G加入式(7)右边，将Fr修改为

加入G后，就可改变离子的径向受力。只要施力适当，就可减小离子的横向速度或能量，从而使原来横向分布较松散的离子向轴心靠拢，达到抑制束晕-混沌的目的。

通过编制 PIC(particle-in-cell)程序对式(4)–(8)进行数值计算，可获得束晕-混沌控制结果。本文的研究分为两部分：一是离子束径向密度与控制信息的选取区域的关系，二是离子束径向密度与填充因子的关系。首先，把半径am≤ r ≤ 1.4am的圆环等分为72份，每份对应的圆心角为5º，对这些区域内离子数Na′逐一取为控制信息，研究控制信息区域与离子束束流品质的关系。然后，改变填充因子，观察磁场大小的改变对束流品质的影响。

2 结果和讨论

2.1 数值模拟参数

为减小离子数密度分布的涨落，并与已有研究结果比较，模拟离子数取 N=5×105，模拟周期取1500。系统参数有：失匹配因子M，其度量一个实际系统与理想系统的偏离，本文定义为束流的初始半径与匹配半径之比，M=rb(0)/am=1.5；调谐衰减因子η，η=1/(am2o0) =0.8，表示空间电荷效应的强弱，其中 o0为真空相移，o0=100º；填充因子 Γ分别取0.8和 0.64，由此可算出无量纲的匹配半径 am=0.8462844，广义导流系数K=0.7853982。用n表示离子数的径向密度，r表示无量纲的束横截面半径。

2.2 数值模拟结果

2.2.1 填充因子Γ=0.8时的模拟结果

把所介绍的区域逐一作为探测离子数 Na′的区域，进行束晕-混沌控制的模拟研究。结果显示，离子束径向密度分布曲线相似，这是因为：(1)采用的离子束和聚焦磁场系轴对称；(2)离子在加速器管道中绕轴线旋转[17]；(3)模拟系统采用的离子个数多，可克服离子数在各个方向的统计涨落。由于密度曲线类似，我们以 175º–180º圆心角区域内的离子数为控制信息进行束晕-混沌控制所对应的径向密度曲线为代表，给出图2、图3。图2为不同角度的观察效果。图3是从前400周期和后400周期内任意抽出部分周期的密度曲线。

由图 2，离子束的径向密度在管道中心基本呈均匀分布，无峰值出现；随着离子束在加速器管道中的传输，束边沿处密度下降至零的速度呈加快趋势；从图2(b)可见，在前400周期内，不同周期的离子束径向密度曲线变化很大，中心密度的最小值约为 1.1×105，最大值约为3.1×105，相差约3倍；后400周期，中心密度的值变化很小，离子束的密度分布变得稳定；离子束分布的范围逐渐减小，从r=1.4变到r=0.95；500周期后，离子束基本被控制在半径r=0.95内。

2.2.2 填充因子Γ=0.64时的模拟结果

当填充因子取值为0.64时，选择半径am ≤r≤1.4 am、圆心角为175º–180º扇形区域作为探测控制信息的区域，作出离子束的径向密度曲线(图4)。将图4和图2进行比较，两者相似，虽然聚焦磁场大小的改变了，但离子束的径向密度依然呈基本均匀分布状态，只不过离子束中心的密度值变化大些。

本文还模拟了Γ=0.4时的情况。此参数下，不能控制束晕-混沌现象，离子束的径向密度虽呈基本均匀分布，但离子的分布范围越来越大。

图2 填充因子Γ=0.8时离子束径向密度的时空演化曲线Fig.2 Evolution of radial density of the ion beams at the filling factor of Γ=0.8.

图3 部分周期处的径向密度曲线Fig.3 Partial evolution of radial density of the ion beams.

2.3 模拟结果分析

把本研究结果与同样以离子数比为控制变量的文献[10]相比，它给出的密度曲线是开始束的中心密度分布变化平缓，600周期后，呈现变化剧烈的状况，甚至有峰值出现，而本研究结果表明，加入控制器后，在前400周期内，离子束的中心密度值虽变化剧烈，但呈现均匀分布；在400周期后，离子束的径向密度的分布变得均匀稳定，达到了很好的控制束晕-混沌效果。前400周期密度值出现剧烈震荡现象，与束晕-混沌是一种非线性极强的时空混沌有关，要控制住束晕-混沌，则需要一段时间。离子束进入加速器管道后，在受到聚焦力、自生场力和外加的非线性力的作用后，离子的运动会发生很大的变化，离子将重新分布，经过一段时间，束晕-混沌已被控制，离子的分布趋于稳定。由此可见，将获取控制信息的区域缩小，不但有利于探测控制信息，而且受到控制后束流变得更加均匀和稳定，再次说明了离子束径向密度的分布与控制信息的选取有关。

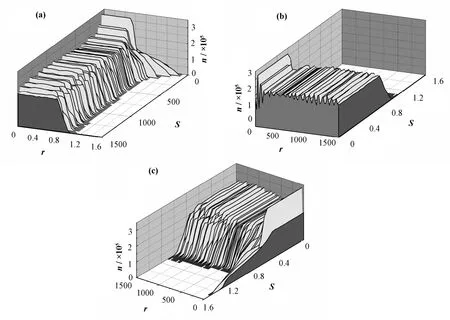
图4 填充因子Γ=0.64时离子束径向密度的时空演化曲线Fig.4 Evolution of radial density of the ion beams at the filling factor of Γ=0.64.

3 结束语

综上所述，以匹配半径外特定小区域内的离子数为控制信息进行束晕-混沌的控制，离子束的径向密度呈基本均匀分布状态，无峰值出现，且与选取控制信息的区域无明显关系，这可为应用强流离子束时确定探测器和靶材料的位置提供参考。

1 郑明光, 叶成, 韩旭.核技术, 2010, 33(2): 81–86 ZHENG Mingguang, YE Cheng, HAN Xu.Nucl Tech,2010, 33(2): 81–86

2 丁大钊.科技导报, 1997, (3): 32–34 DING Dazhao.Science and Technology Review, 1997,(3): 32–34

3 方锦清.自然杂志, 2000, 22(2): 63–69 FANG Jinqing.Natrue, 2000, 22(2): 63–69

4 方锦清, 陈关荣.物理学进展, 2003, 23(3): 321–388 FANG Jinqing, CHEN Guanrong.Progress in Physics,2003, 23(3): 321–388

5 方锦清, 陈关荣.强激光与粒子束, 2000, 12(5):647–651 FANG Jinqing, CHEN Guanrong.High Power Laser and Particle Beams, 2000, 12(5): 647–651

6 方锦清, 高远, 翁甲强, 等.物理学报, 2001, 50(3):435–439 FANG Jinqing, GAO Yuan, WENG Jiaqiang, et al.Acta Phys Sin, 2001, 50(3):435–439

7 朱伦武, 翁甲强, 高远, 等.物理学报, 2002, 51(7):1483–1488 ZHU Lunwu, WENG Jiaqiang, GAO Yuan, et al.Acta Phys Sin, 2002, 51(7): 1483–1488

8 刘萍, 翁甲强, 廖高华, 等.原子能科学技术, 2006,40(4):460–464 LIU Ping, WENG Jiaqiang, LIAO Gaohua, et al.Atomic Energy Science and Technology, 2006,40(4):460–464

9 杨翠云, 翁甲强, 刘海英, 等.物理学报, 2008, 57(11):6883–6887 YANG Cuiyun, WENG Jiaqiang, LIU Haiying, et al.Acta Phys Sin, 2008, 57(11): 6883–6887

10 高天附, 翁甲强.广西物理, 2005, 26(3):4–7 GAO Tianfu, WENG Jiaqiang.Guangxi Wuli, 2005, 26(3):4–7

11 陈志波, 翁甲强, 余海军.广西师范大学学报(自然科学版), 2007, 25(1): 9–12 CHEN Zhibo, WENG Jiaqiang, YU Haijun.Journal of Guangxi Normal University (Natural Science Edition),2007, 25(1): 9–12

12 白龙, 翁甲强, 方锦清, 等.物理学报, 2004, 53(12):4126–4130 BAI Long, WENG Jiaqiang, FANG Jinqing, et al.Acta Phys Sin, 2004, 53(12):4126–4130

13 高天附, 翁甲强, 田敬北.广西师范大学学报(自然科学版), 2006, 24(1): 5–8 GAO Tianfu, WENG Jiaqiang, TIAN Jingbei.Journal of Guangxi Normal University (Natural Science Edition),2006, 24(1): 5–8

14 Masanori Ikegami.Phys Rev E, 1999, 59(2): 2330–2338

15 Fink Y, Chen C, Marable W P.Phys Rev E, 1997, 55(6):7557–7564

16 Chen C, Davidson R C.Phy Rev Lett, 1994, 72(14):2195–2198

17 廖高华, 翁甲强, 成丽春, 等.物理学报, 2005, 54(1):35–42 LIAO Gaohua, WENG Jiaqiang, CHEN Lichun, et al.Acta Phys Sin, 2005, 54(1): 35–42