3He多球中子谱仪响应函数的理论模拟
魏熙晔 袁永刚
(中国工程物理研究院核物理与化学研究所 绵阳 621900)
在反应堆、中子管、中子发生器、核素中子源等中子源的研究中,中子辐射场的能谱测量对于核物理实验及辐射防护十分重要。根据不同能量中子和不同需求,发展了多种中子测谱法,如阈探测器法、核反应法、晶体衍射法、反冲质子法和飞行时间法。然而,核设施装置周围物质对中子散射、慢化,会使场点中子能谱发生严重退化,且不同场点的中子谱的差异较大,上述中子测谱法均有局限性。多球中子谱仪(Multisphere Neutron Spectrometer)法是唯一可覆盖热中子至高能中子的探测方法。
多球中子谱仪由Bramblett等[1]于1960年首次用于中子能谱测量。在中子辐射防护中,多球中子谱仪具有函数简单、测量范围广(从热能区到几十兆伏)、各向同性、高灵敏度(剂量当量率达 1 μSv·h–1)、对电子学噪声和光子计数的甄别功能较好等优点,成为非常适合的测量工具。Mares等[2,3]计算了3He正比管多球中子谱仪中子响应函数,分析了实验与计算的误差因素,并用改善的截面数据库和软件,提高6LiI闪烁体和3He正比管多球中子谱仪的响应函数模拟精度。Aroua等[4]利用标定、模拟和验证对多球中子谱仪的响应函数进行了评估和测试。Vega-Carrillo等[5,6]用蒙特卡罗法模拟了热中子到20 MeV中子的6LiF多球中子谱仪响应函数;Vega-Carrillo等[7]模拟了3He正比管的多球中子谱仪响应函数。Mallett等[8]完成了洛斯阿拉莫斯实验室(LANL)的多球谱仪系统标定,并对不同方法构建的初始谱的进行了解析。Sweezy等[9]比较了6LiF与7LiF多球谱仪与6LiI(Eu)多球谱仪在Georgia技术研究堆中子能谱的测量结果,并比较了能谱解析与MCNP模拟优化的结果。
根据中子能谱和响应函数的解析关系,能谱解析是逆问题的求解,响应函数的误差会导致中子注量谱产生不可接受的误差。但是,精确的响应函数和解谱问题,至今未有特别完善的解决,多球中子谱仪的重要参数对响应函数的理论研究,值得深入探讨。
多球中子谱仪的中子响应函数可由在单能中子场中的标定实验或Monte Carlo模拟获得。实验测量的局限性,有可用单能中子源有限、建筑物和空气散射、几何效应(中子源弱及球响应低)等;M-C法的误差来源于截面数据库的精度、能量分隔、几何模型精度及方差缩减影响。
1 理论模型与计算原理
1.1 计算模型与谱仪响应
中子多球谱仪的能谱测量关系为:
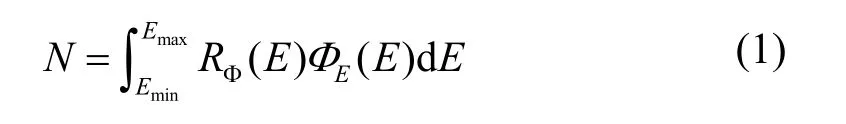
式中,N为中子计数,Emax、Emin分别为待测中子能量上下限,RΦ为响应函数,Φ(E)为中子能谱。获取中子响应函数后,根据探测器计数测量结果,通过解谱得到中子能谱。
多球谱仪慢化体采用聚乙烯材料,不锈钢球壳充高压3He气体,平行中子束从平板源入射到多球谱仪上(图1)。在中子传输计算中,中子与3He作用主要有三种反应截面:总截面σ(n,total)、弹性散射截面σ(n,n)和3He(n,p)3T反应截面σ(n,p),不同能量中子束与3He各反应截面如图2所示。文献[8]综合考虑了不同能量中子的传输与慢化机制,结合现有堆上测量的限制条件,确定多球谱仪的聚乙烯(PE)的慢化体直径为:0(裸球), 5, 6.5, 8, 10, 12, 14, 17, 20,24, 28, 34 cm;不锈钢球壳(含70.5% Fe、19.5% Cr、10% Ni)的内外半径为1.50 cm和 1.55 cm;内充200 kPa3He,原子密度为 5×1019atoms·cm–3,3He 密度为 2.5041×10–4g/cm3(NA=6.0221×1023atoms·mol–1,M=3.01603 g)。
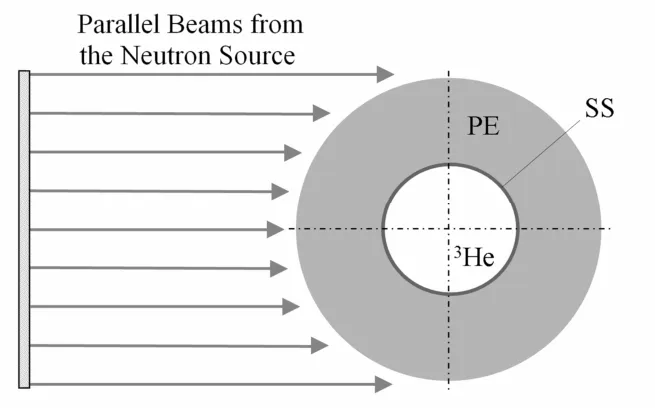
图1 多球谱仪响应函数计算模型Fig.1 The simulation model for multisphere neutron spectrometer.
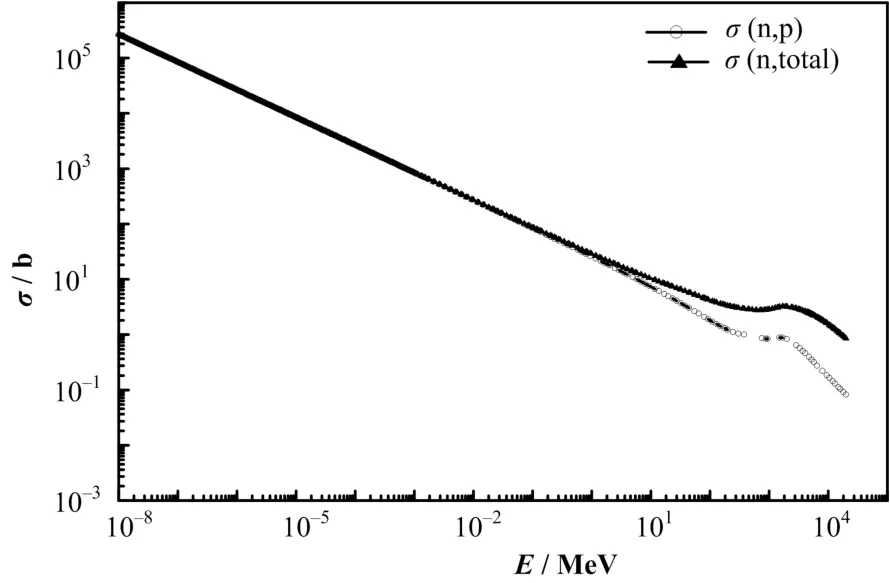
图2 中子束与3He的反应截面Fig.2 Neutron reaction cross sections for 3He.
1.2 响应函数模拟
谱仪响应函数定义为从平行源项发出的单位入射中子注量(即归一化注量)造成的反应数,其表达式为

式中,V为3He探测器灵敏体积(cm3);C为归一化因子,取 C 为原子密度(atoms·b–1·cm–1);Φ(E)为注量(cm–2);σ(E)为各反应通道的截面(b);RΦ(E)为响应函数,即单位注射平行中子注量在灵敏体积内与3He 发生的反应率(reactions·cm2)。
该多球中子谱仪响应函数模拟程序为MCNP/4C[10],用F4卡与FM卡计算不同通道的反应率。F4用于计算经过一个栅元的平均注量,采用径迹长度法模拟体注量,即记录粒子在探测器中的径迹长度,探测器体积内平均注量为:
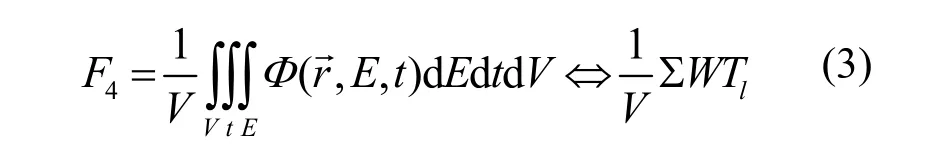
式中,F4为栅元体积V内r的 平均注量,W为粒子权重,Tl为径迹长度,(,E,t )为粒子注量。粒子每次散射到下次碰撞前,记录其在V内的径迹长度(乘以权重),在选定栅元体积、指定时间和能量范围内对所有粒子径迹WTl/V累加,即得F4。
对于不同反应率通道的计算需要用到 FMn(n是记数号)记数乘子卡,给出物质号、探测器计数号、归一化因子以及相应的反应率通道后,可计算给定通道反应率。FM4是对应F4卡用于计算不同反应通道而设定的,其格式为:FM4 C M R,其中,C为归一化因子;M为对应的m卡的材料序号;R为对应的反应率通道号。
2 响应函数模拟结果
2.1 自由气体热处理和S(α, β)散射处理
自由气体模型假定介质为自由气体,近似考虑为热中子运动,在零温时弹性散射截面与能量近似无关,反应截面与温度也近似无关。自由气体热处理(Free gas thermal treatment)包括校正弹性散射截面和在碰撞运动学计算时考虑靶核的速度。当S(α, β)处理条件不满足时,粒子只是经历弹性或非弹性碰撞,弹性碰撞的截面的概率为
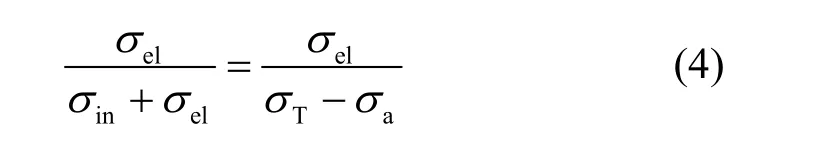
其中,σel为弹性碰撞截面;σin为非弹性碰撞截面;σa为吸收截面;σT为总截面;非弹性碰撞的截面的概率为 σin/(σT–σa)。
S(α, β)散射处理是中子与物质的分子和晶格完整作用,主要考虑:(1) 非弹性散射截面σin和耦合的能量角度取决于S(α,β)散射定律;(2) 弹性散射对于出射中子的经历没有变化,弹性散射截面σel和角分布取决于晶格参数。
MT卡是对应材料卡(M卡)用于S(α,β)散射识别设定的,热中子 S(α,β)截面数据库并非必需,但对于中子热化的研究非常重要,其数据表包括分子和晶格结构的热中子散射。MCNP包括部分核素的S(α,β)截面数据,聚乙烯对应的 S(α,β)截面数据可以使用,通过MT卡的应用可以使用热中子数据库的S(α,β)散射截面。不采用 S(α,β)散射处理(自由气体热处理)与采用S(α,β)散射处理结果如图3所示。
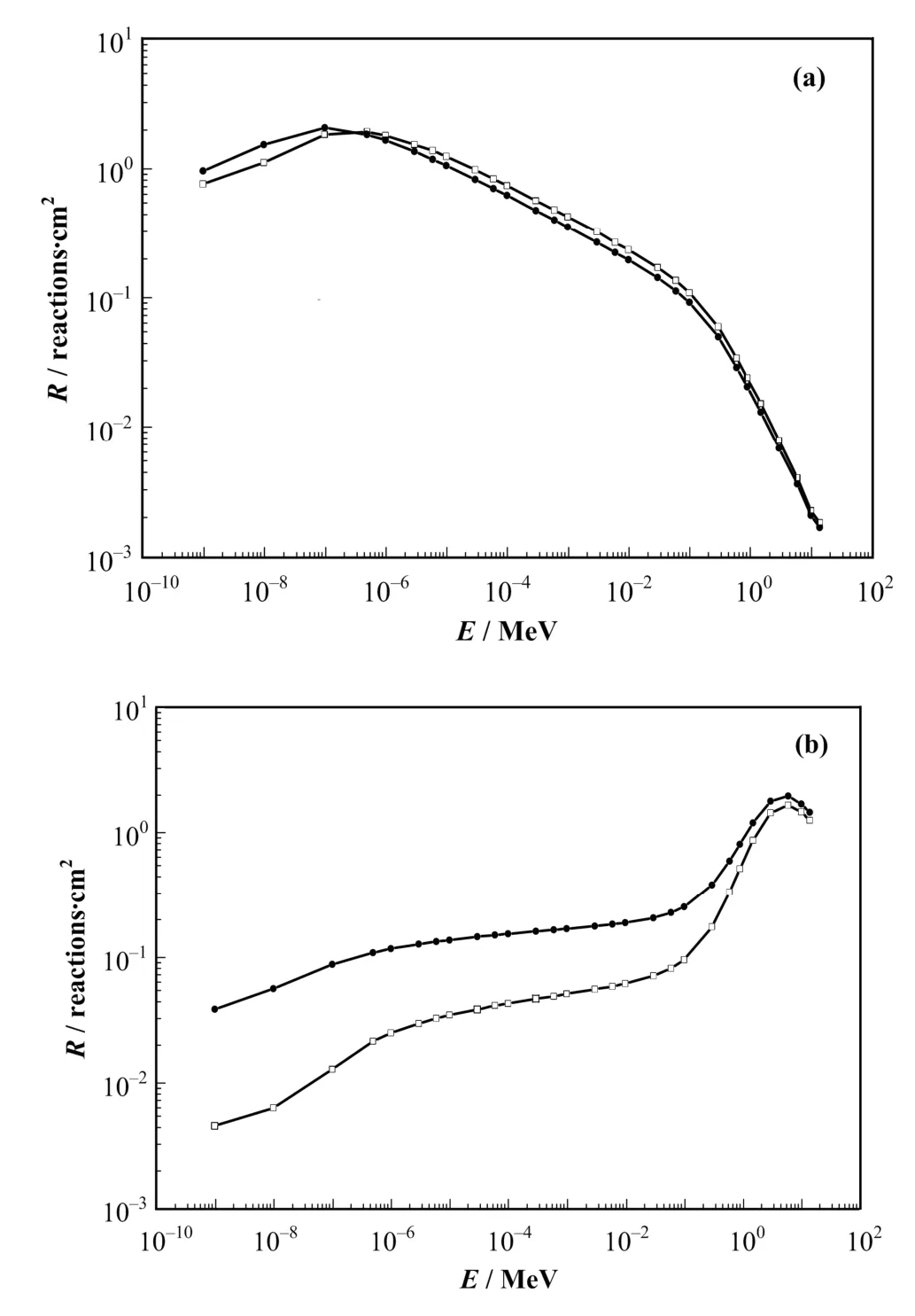
图3 采用(□)与不采用(●)S(α, β)散射处理的结果比较Fig.3 Response results with (□) and without (●) S(α, β)scattering treatment.
MCNP采用连续能量的核与原子数据库,其主要来源是 ENDF、ACTI、ENDL、EPDL和 ACTL等核数据库。核数据表包括中子反应、中子引致的光子、光子反应、中子剂量与活化,以及热中子S(α,β)散射反应。ENDF为MCNP提供了部分的S(α, β)截面数据,对于MCNP未提供材料的S(α, β)截面数据,可由NJOY程序转换成MCNP可用的数据格式。
自由气体模型对于多数问题均能取得满意的结果,但对于热中子散射采用 S(α,β)散射处理是必需的,S(α,β)散射处理的中子能量范围为 10–5–4 eV。
2.2 不同反应通道的结果比较
用(n,total)、(n,p)截面对PE厚度分别为0, 5, 34 cm的谱仪响应函数计算结果如图4所示。
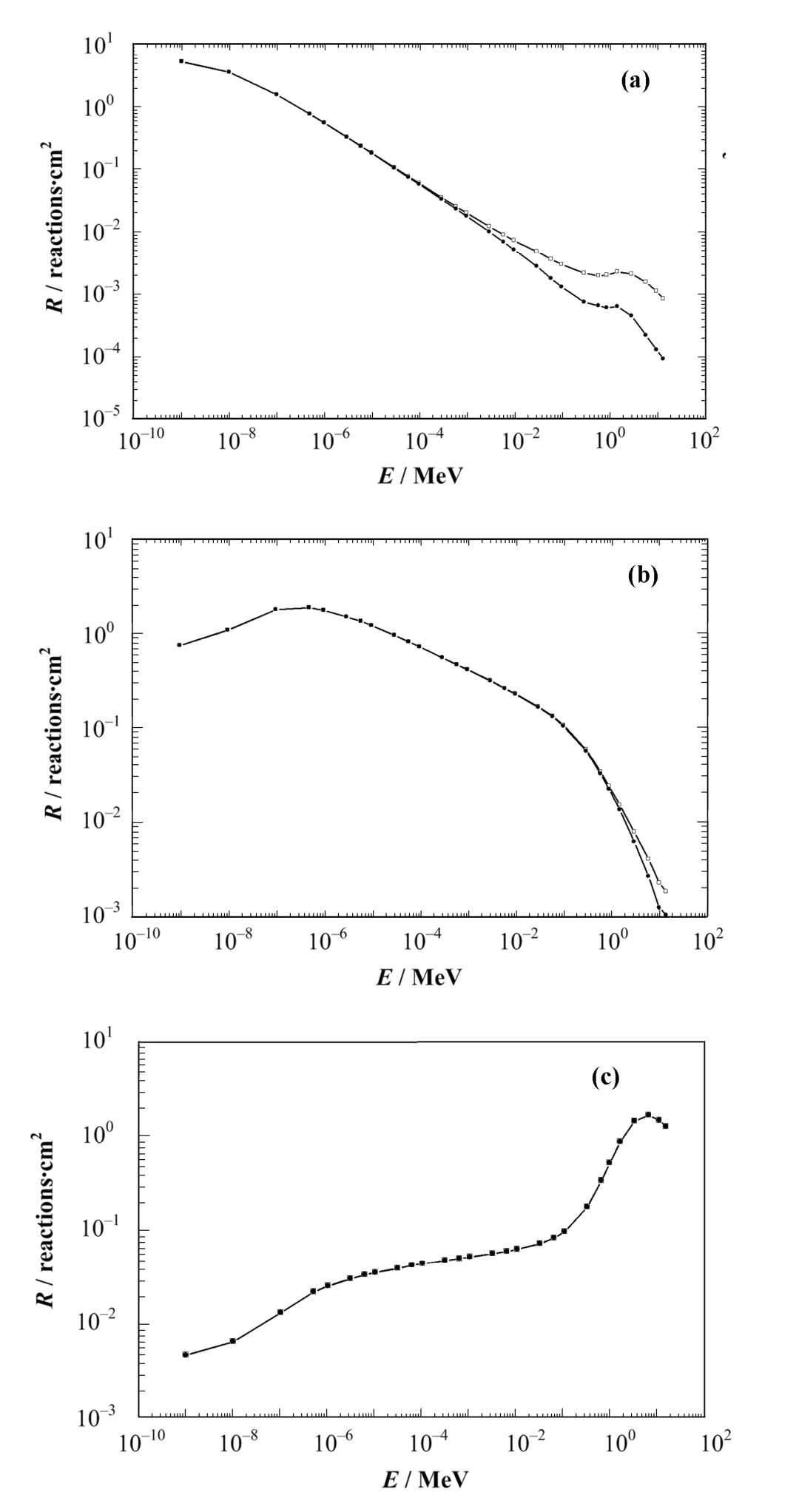
图4 用(n,p)通道(□)与(n,total)通道(●)计算结果(Fig.4 Response results of the (n,p) reaction channel (□) and(n,total) reaction channel (●).
2.3 采用S(α,β)与(n,total)截面处理结果
对于文献[7]中的多球谱仪参数,分别采用不同通道及热中子处理模式计算并与文献[7]结果进行了比较。图 5给出用(n,p)(或(n,total))通道计算的响应结果与Vega-Carrillo等[7]所获结果的比较(裸球),RM(n,p)、RM(n,total)分别是用(n,p)与(n,total)通道计算结果,RV为Vega-Carrillo等计算结果。图6给出采用(或不采用)S(α,β)散射处理结果与文献[7]的响应结果比较(慢化球直径d=7.62 cm),RM1、RM2分别是采用与不采用 S(α,β)散射处理结果,图 6采用的均为(n,total)反应通道。结果表明,对于采用 S(α,β)散射处理与(n,total)截面的响应函数,计算结果与文献[7]结果十分吻合,验证了计算方法的可靠性。

图5 采用(n,p)与(n,total)通道的响应函数(裸球),RV为文献[7]结果Fig.5 Responses at d=0, using (n,p) and (n,total) reaction channels,.and comparison with Ref.[7] (RV).
用(n,total)通道与 S(α,β)散射处理计算了自主设计的不同直径聚乙烯慢化体3He多球谱仪响应函数,图7直观的显示了不同直径慢化体对于不同能量中子响应的特性,具体结果列于表1。

图6 S(α,β)散射处理采用(RM1)与不采用(RM2)的响应函数,(n,total)通道,d=7.62 cm,RV为文献[7]结果Fig.6 Responses at d=7.62 cm,using (n,total) reaction channel with (RM1) and without (RM2) the S(α,β) scattering treatment,and comparison with Ref.[7] (RV).
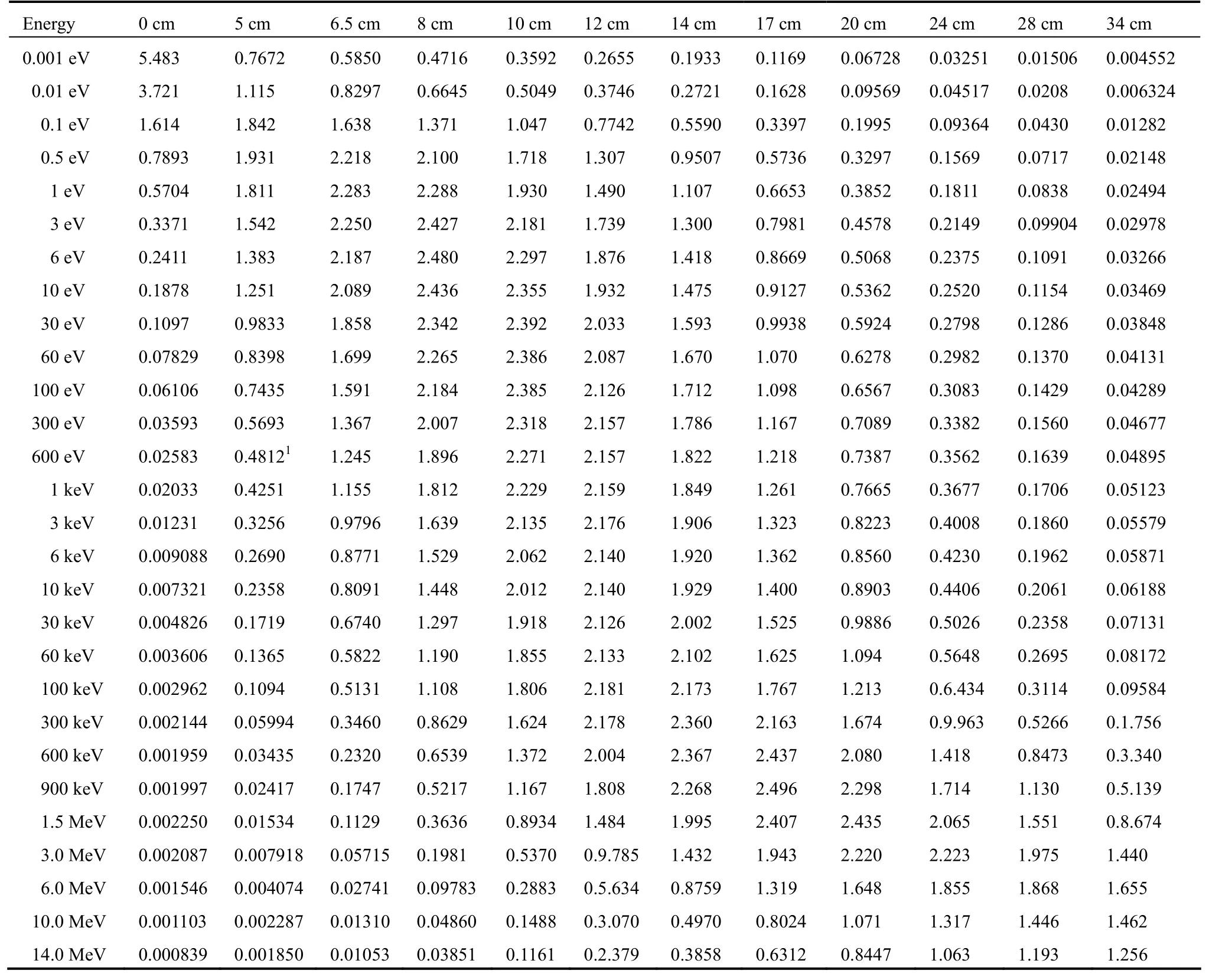
表1 不同直径的多球3He中子谱仪响应函数(单位:reactions·cm2,不确定度≤1 %)Table 1 Response function (in reactions·cm2, with uncertanties≤1 %) of 3He multisphere neutron spectrometer of different d.
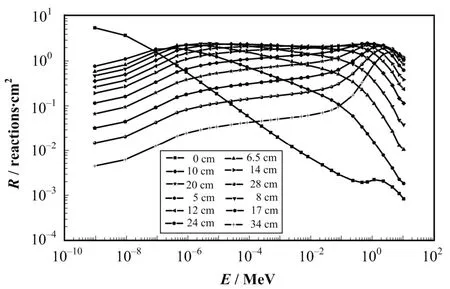
图7 采用(n,total)通道与S(α, β)散射处理计算结果(d 为慢化体直径)Fig.7 Response results with (n,total) reaction channel and S(α,β) scattering treatment(d is diameter of the moderator)
3 讨论
(1) 响应函数绝对量问题。文献[5]与文献[3]以及文献[5]与 Cruzate[11]给出的响应函数绝对值均出现不一致情况,其相对值符合的很好。Cruzate认为差异是采用不同截面数据库引起的,本文认为截面数据库不是主要因素。通过分析认为,其绝对量不一致的原因可能是:灵敏体积是否归一、反应通道是否一致、热中子处理模式以及计算方法差异等。本文在充分考虑到式(3)归一化常数 C(即原子密度)、灵敏体积和单位注量归一化等因素后,得到了响应函数的绝对量。
(2) 自由气体热处理模型对低能中子响应结果的不一致性。自由气体热处理模型对于厚度较小的聚乙烯在中子能量较高时计算结果较好,但对于低能中子部分(如<10–6MeV),对响应函数计算结果影响较大;而对于直径34 cm聚乙烯慢化体,由于对中子慢化作用明显,采用自由气体模型与采用S(α,β)散射处理在入射中子能量很高时,计算结果差别很大,采用S(α,β)散射处理就十分必要。
(3) 不同反应通道计算结果。对于裸球,采用(n,p)通道与(n,total)通道计算结果与图 2的(n,p)与(n,total)反应截面图形形状一致,与实际结果符合。对于具有一定厚度(如直径为5 cm)的聚乙烯球,由于聚乙烯对中子慢化造成能谱退化,而不同能量中子与3He作用截面差别很大,采用(n,p)通道与(n,total)通道在中子能量较高时会不一致;当聚乙烯直径厚到一定程度(如直径34 cm),中子慢化足够充分时,采用(n,p)通道与(n,total)通道计算结果一致。
(4) 方差处理情况。MCNP给出了加权法、截断法、俄罗斯轮盘赌与分裂等方差缩减技术。文献[6]中,为降低方差,采用区域重要性等方差缩减技术,可以提高计算效率。方差处理方法使用不当会影响计算结果精度,目前暂未使用方差缩减技术。
(5) 响应计算结果的初步检验。对于能量较高的中子入射到裸球上,由于不锈钢球与中子作用截面较低,可直接用Nσ(3He原子总数与截面的乘积)来估计响应结果。如14 MeV中子响应计算结果为8.268×10–4reactions·cm2,而程序计算结果为 8.390×10–4reactions·cm2;对于低能中子,由于裸球外不锈钢也会改变入射中子能谱,就不能用 Nσ来估计响应结果。
4 结论
由本文以不同反应通道采用 S(α,β)散射处理对响应函数的计算,可得如下结论:
(1) 不采用 S(α,β)散射处理会造成低能中子响应结果的不一致性,对于低能中子的热化处理,需要考虑 S(α,β)散射的问题。
(2) 不同反应通道(n,total)、(n,p)截面对裸球和聚乙烯慢化体谱仪响应函数具有不同影响,为计算总响应结果,应采用(n,total)通道计算。
(3) 采用文献中的多球谱仪参数对于利用S(α,β)散射处理与(n,total)截面的响应函数,计算结果与Vega-Carrillo等计算结果十分吻合,验证了计算方法的可靠性,并解决了绝对量模拟问题。对于裸球模拟计算结果与根据截面直接估计结果基本一致,并提出了物理解释,进一步验证了方法的可靠性。
(4) 采用 S(α,β)散射处理与(n,total)截面处理结果,对自主设计的多球谱仪响应函数进行了计算,与理论分析结果符合。
1 Bramblett R L, Ewing R I and Bonner T W.Nucl Instr.Meth, 1960, 9: 1–12
2 Mares V, Schraube G, and Schraube H.Nucl Instrum Methods Phys Res Sect A, 1991, 307: 398–412
3 Mares V, Schraube H.Nucl Instrum Methods Phys Res Sect A, 1995, 366: 203–206
4 Aroua A, Grecescu M, Lerch P, et al.Nucl Instrum Methods Phys Res Sect A, 1992, 321: 298–315
5 Vega-Carrillo H R, Wehring B W, Veinot K G, et al.Radiation Protection Dosimetry, 1999, 81(2): 133–140
6 Vega-Carrillo H R.Radiation Measurements, 2002, 35:251–254
7 Vega-Carrillo H R, Manzanares-Acuna E.Revista Mexicana De Fisica.2005, 51(1):47–52
8 Mallett M W, Mclean T D, Olsher R H, et al.Radiation Protection Dosimetry, 2004, 110(1–4): 549–553
9 Sweezy J E, Hertel N E, Veinor K G, et al.Radiation Protection Dosimetry, 1998, 78(4): 263–272
10 Briesmeister J F.MCNP―A General Monte Carlo N-Particle Transport Code [R].Los Alamos National Laboratory Report, LA-13709-M, Version4C, US: March 2000
11 Cruzate J A, Gregori B N, Papadopulos S B, et al.Multisphere neutron spectrometric system with thermoluminescent detecors.The 10thInternational Congress of the International Radiation Protection Association -IRPA, Hiroshima, Japan, 2000

