SNIP法在天然放射性核素g能谱分析中的应用

吴和喜 刘庆成 杨 波 刘玉娟

1（东华理工大学核资源与环境教育部重点实验室 南昌 330013）

2（东华理工大学核工程技术学院 抚州 344000）

由于探测器产生的离子对(或空穴-电子对)的统计涨落、探测器的边缘效应、电子电路的弹道亏损，以及脉冲堆积效应等形成g射线峰，与g射线与物质的相互作用而形成的康普顿坪、单逃逸峰、双逃逸峰、反散射峰等构成g能谱。用 g射线能谱可对待测样品进行定性、定量分析。对谱仪作能量刻度、效率刻度、峰型/半高宽刻度后，便可由核素全能峰净面积作该元素的定量分析。全能峰净面积计算，则须确定峰位与峰区，并在峰区扣除本底，去除高能 g射线康普顿坪、g射线在探测器灵敏体积内的小角度散射[2]等影响。确定峰位与峰区的方法中，以对称零面积找峰法为最优[2–4]。本底扣除方法主要有：光滑谱数据梯形法、指数函数拟合法、多项式最小二乘法拟合等。这些本底扣除法并无明显缺陷，然而，若峰区的全能峰上叠加有散射峰、本底峰(实验室环境中天然放射源或污染物产生的g射线全能峰[2])、或屏蔽体物质的特征X射线峰，计算结果就会产生较大误差。而若边界道的统计涨落较大，则对峰区确定和净峰面积计算结果的影响甚大。本文介绍一种全谱基底扣除方法(Sensitive nonlinear iterative peak, SNIP)法[5–8]，其能有效估算峰区确定、本底扣除、散射峰、本底峰及特征X射线峰等对全能峰净面积计算的影响。

1 理论依据

为减小各道计数的大范围变动，将各道计数作式(1)变换：

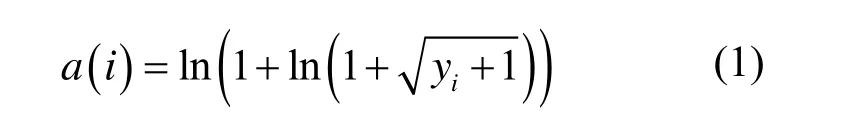
其中，yi表示原谱数据第i道计数，a(i)表示变换后第i道数值。

在峰区确定中，边界道计数统计涨落对峰区的确定存在影响。消除统计涨落的影响可用重心法、多项式最小二乘拟合法、傅立叶变换法、离散函数积变换等[2]。本文用重心法。但是，对于一个峰谷，其左右两道的重心会大于峰谷道的计数，导致所得计数大于原始计数，为此定义经过一次平滑后第 i道数值如下：

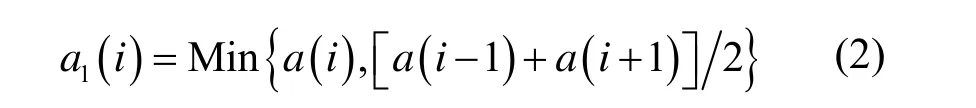
对一次平滑后的谱数据再作平滑，在边界道，将消除其附近各道的统计涨落的影响，使峰边界向真实边界移动；在峰区进一步平滑使更接近于本底。此时，可增加滤波窗口宽度、加快滤波速度，则滤波窗口宽度为w=2m+1时，各道数值为：

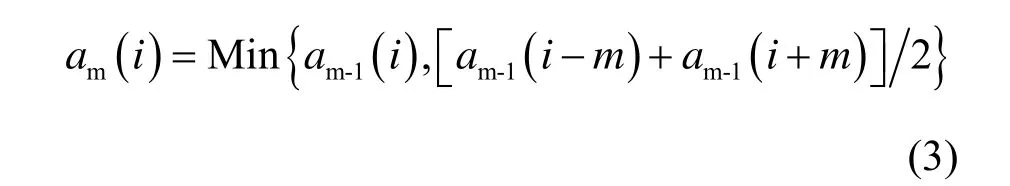
同理，也可得到4、6和8次滤波器的m次迭代各道数值计算公式[5]。由此am(i)值反变换便得各道本底计数(即全谱本底)，扣除全谱本底后，由于在单峰及重叠峰的两侧，净峰计数为零，即可确定峰边界道。

2 实验结果

2.1 实验条件

N型同轴HPGe探测器(美国ORTEC公司)，其相对探测效率40%，对60Co的1.332 MeV的峰的半高宽为1.84 keV，峰康比为60.378/1，对238U、232Th和40K的探测下限分别为20、8、5 Bq/kg。点源(中国原子能科学研究院)：152Eu、60Co；粉末体源(核工业北京地质研究院)：40K源、232Th平衡源、U-Ra平衡源。K、Th、U标准物质各一个。

2.2 本底扣除效果

用滤波窗宽度w=5、25、45、65和85，对60Co点源所测g能谱进行本底计算，结果表明(图1)，滤波窗宽度越窄，越有利于减弱本底峰、散射射线峰及屏蔽材料的特征X射线峰的影响。但本底抑制过量，全能峰面积的削减幅度较大。

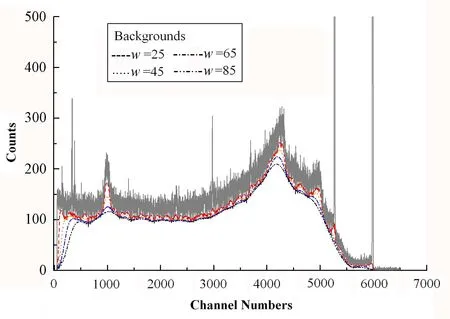
图1 用二次滤波函数和滤波窗w=5, 25,45, 65, 85对60Co点源 g谱的本底计算Fig.1 Measured 60Co g-ray spectrum and the calculated backgrounds using 2nd-order filtering at different window widths (w).

对152Eu点源所测 g能谱，滤波窗口宽度为w=105，用2、4、6和8次滤波函数进行能谱本底计算表明(图 2), 高滤波次数对本底的扣除有较好效果。

对40K源、232Th平衡源以及U-Ra平衡源混合粉末体源进行测量，取其测量谱线中的一段，对所取谱段进行本底扣除，结果见图 3。除峰区内有计数外，边界道计数均为零。可见 SNIP法能有效扣除本底，确定峰区边界。

图2 用2/4/6/8次滤波函数对点状152Eu源 g谱本底计算结果(w=105)Fig.2 Measured 152Eu g-ray spectrum and the calculated backgrounds using filtering of different orders at w=105.

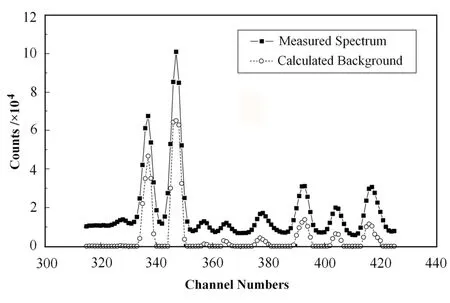
图3 用6次滤波函数(w=31)对U-Ra-Th-K混合粉末平衡源 g能谱的一段谱线作本底去除Fig.3 A section of g-ray spectrum measured with radioactive U-Ra-Th-K, and the background using 6th-order filtering at w=31.

2.3 238U、232Th、40K放射性比活度的测试结果

我们用93、239及1461 keV的特征 g射线，分析样品中天然放射性核素238U、232Th、40K的比活度。采用4次滤波函数，滤波窗宽度w=11, 15,19, …, 123，对标准源及混合标准物质进行全谱本底扣除。测量结果的相对误差如图4所示。由图4，w极窄时的本底计数过量，全能峰计数损失可观，导致测量结果误差很大；随着w增大，扣除的本底越来越接近于真实的本底值，测量误差逐渐减小；w再增大，则扣除的本底小于真实本底值，也导致测量结果误差增大。但由于 SNIP法采用多次迭代，随着迭代次数的增加，本底计算值变化较小，能稳定在一定的精度范围内，有利于窗口的选择。

图4 天然放射性核素(238U, 232Th, 40K)比活度测量的相对误差(本底扣除：4 次滤波函数，w=11, 15, 19, ··, 123)Fig.4 The relative error in measuring specific activity of natural radionuclides of 238U, 232Th and 40K .The backgrounds were treated with the4th-order filtering at the windows of w=11, 15, 19, ··, 123.

93 keV的特征 g射线受到谱仪屏蔽材料铅的特征X射线的影响很大，从图4可见，对238U的精确测量的迭代次数少于对232Th、40K的精确测量。同理，239 keV g射线受到散射射线峰的影响，对232Th的精确测量所用迭代次数少于对40K的精确测量，三者的测量结果能在一个较大的参数(迭代次数)变化范围内保持一定的精度。用4次滤波函数，在w=23–123时，对238U放射性比活度测量误差小于5%；在w=39–123时，对232Th放射性比活度测量误差小于0.5%；在w=59–123时，对40K放射性比活度测量误差小于 2%。在窗口 w=47–123时，对238U、232Th和40K放射性比活度的测量结果总相对误差均小于8.5%。

3 结语

综上所述，高次滤波函数或滤波窗口较窄的情况下，SNIP方法能有效地抑制基底影响，并对本底峰、散射射线峰及屏蔽材料的特征X射线等本底因素的影响有很强的削弱作用，但同时也会减少全能峰计数。而低次滤波函数及滤波窗口较宽时不但不能对本底计数起到很好的抑制作用，而且增加本底计数对全能峰计数的影响。但由于 SNIP方法采用迭代的方法，随着滤波窗口宽度w的变化，本底拟合值下降越来越缓慢。在一定的精度前提下，对各次滤波函数，分析测试人员均有很大的滤波窗口的选择范围。此范围可以通过针对不同测量核素、样品组成等，分析测试人员对所操作的谱仪进行试验很容易找到。通过实例分析，采用4次滤波函数，在w=23–123时，对238U放射性比活度测量误差小于 5%；在 w=39–123时，对232Th测量误差小于0.5%；在w=59–123时，对40K测量误差小于2%。在滤波窗口w=47–123时，对238U、232Th和40K放射性比活度的测量结果总相对误差均小于8.5%。

1 庞巨丰.g能谱数据处理.陕西科学技术出版社, 1990 PANG Jufeng.Data processing of gamma-ray spectra.Shanxi Science and Technology Publishing Company,1990

2 庞巨丰, 郑桂芳, 侯晓凤.原子能科学技术, 1987, 21(3):270–279 PANG Jufeng, ZHENG Guifang, HOU Xiaofeng.Atomic Energy Science and Technology, 1987, 21(3): 270–279

3 庞巨丰, 郑桂芳.计量学报, 1985, 6(3): 213–220 PANG Jufeng, ZHENG Guifang.Acta Metrologica Sinica,1985, 6(3): 213–220

4 Miroslav Morháč, Ján Kliman, Vladislav Matoušek, et al.Nucl Instr Meth, 1997, A401: 113–132

5 Morháč M, Kliman J, Jandel M, et al.Computer Physics Communications, 2005, 172(1): 19–41

6 Morháč M, Matoušek V, Turzo I, et al.Nuclear Instruments and Methods in Physics, 2006, A559: 76–80

7 Morháč M, Veselský M.Nucl Instr Meth, 2008, A592:434–450

8 Morhac M, Vladislav M.Applied Spectroscopy, 2008,62(1): 91–106