SH波入射时非等腰三角形结构与基础相互作用
邱发强,王慧文,王 雪
(1.中南大学土木建筑学院,长沙410075,rainy95@sina.com;2.厦门市建筑科学研究院集团股份有限公司,福建厦门361004;3.黑龙江工程学院,哈尔滨150050;4.东北林业大学,哈尔滨150040)
近年来,与基础和结构相互作用相关的分析方法有了很大的发展[1].研究范围也从高层建筑逐步扩展到核电站的反应堆建筑、水坝、海洋平台、桥梁等一系列建筑物[2].建立二维反平面模型的波动方程,解决建筑物与基础的相互作用问题已经取得了不少成果[3-8].
本文利用波动方程的复变函数理论[9],采用移动坐标的方法求解了非等腰三角形坝体结构与基础相互作用的问题,给出了分析例题和数值结果.
1 问题的表述
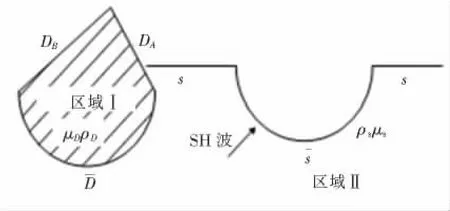
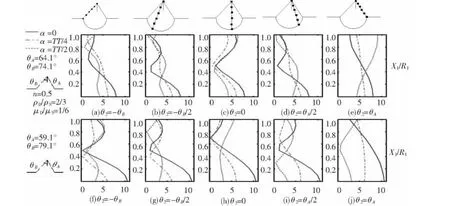
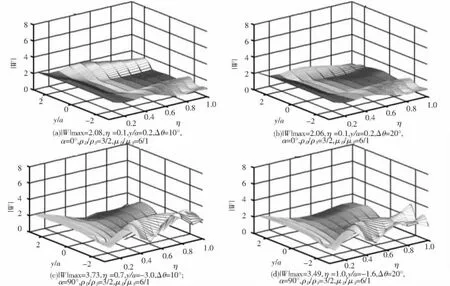
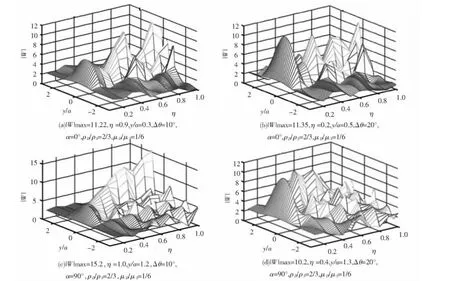
非等腰三角形结构如图1所示,图中三角形凸起顶点记为O1,两边边界分别记为DA,DB,坡度分别为1:n1,1:n2(n1 图1 非等腰三角凸起结构示意图 图2 模型分区示意图 在I区内,以三角形顶点O1和底边中点O为原点分别建立Cartesian坐标系,记为X-O-Y,X1-O1-Y1,分别对应复平面和其中O1x1轴为顶角平分线,如图1所示.在区域I内构造的满足三角形斜边应力自由的驻波函数WD可表示为 式(1),(2)中, 式(2)即为在区域I中,满足斜边应力自由的驻波函数,其相应的应力表达式为 其中: 在区域II内,满足半空间表面应力的自由散射波W(S)及相应的应力为 其中: 而入射波和反射波及相应的应力可写为 根据“契合”思想,在公共边界D上应该满足位移和应力连续条件.即 利用位移和应力的正弦、余弦部分一一对应关系进行傅里叶展开,有 其中: 由于入射SH波的作用,区域I内的驻波为WD,而弹性半空间区域II中的总波场则可以写成 而入射波的频率ω可与区域I中半圆的半径a组合成为入射波波数,即入射波波数为 作为算例,假设三角形底边的一半a=1.0,y/a=±1表示凸起地形与水平面的相交位置,y/a= Δ对应着凸起地形的顶点,而|y/a|<1.0和|y/a|> 1.0则分别代表凸起地形和水平面上各点的位移幅值. 图3和图4分别给出了结构相对基础较“软”(ρD/ρS= 2/3,μD/μS= 1/6)和 较“硬”(ρD/ρS=3/2,μD/μS=6)情况下,η=0.5的入射波以α=0°,45°,90°入射,顶角138.2°,Δθ=θB-θA=10°或20°的结构内各特征点的位移幅值;图5和图6则分别给出了结构相对基础较“软”和较“硬”情况下,入射波以α=0°入射,顶角138.2°,Δθ=10°或20°的坝体结构表面位移幅值变化三维图. 图3 相对基础较"软"的结构位移幅值 图4 相对基础较"硬"的结构位移幅值 图5 垂直和水平入射时相对基础较"硬"的结构表面位移幅值三维图 图6 垂直和水平入射时相对基础较"软"的结构表面位移幅值三维图 1)当SH波垂直入射时,图3和5表明“软”结构的地表最大位移幅值总是出现在顶点附近(Δθ= 10°,y/a=0.3;Δθ=20°,y/a=0.5);图4和6表明“硬”结构的地表最大位移幅值则总是出现在顶点的左侧结构表面(对于Δθ=10°,-1.0≤y/a≤0.3;对于Δθ=20°,-1.0≤y/a≤0.5). 2)由图5到图6可知,“软”坝结构的表面位移幅值远远大于“硬”坝.当Δθ=10°时,“软”、“硬”坝结构的|W|max分别为15.2和3.73且都出现在α=90°,相差4.075倍;当Δθ=20°时,“软”坝结构的|W|max为11.35(α=0°)和“硬”坝为3.49(α=90°)相差3.25倍. 1)对于非等腰三角形结构,波数、入射角等入射波的物理参数对结构表面位移的影响非常显著.结构对SH波在弹性空间传播的影响突出,较“软”的结构相对较“硬”的结构吸收“能量”较多,反射“能量”水平差,从而影响结构表面位移幅值大小差异及出现地点的不同. 2)本文提供的方法理论上没有问题,但采用的计算方法适用于三角形顶角>60°的情况,顶角越大精度越高.顶角<60°的情况需要另外研究其计算方法. [1] 胡聿贤.地震工程学[M].北京:地震出版社,2006. [2] 申爱国.土-结构动力相互作用研究及其应用[D].大连:大连理工大学,1996. [3] 林皋,关飞.结构-地基相互作用对重力坝地震反应的影响[J].地震工程与工程振动,1991,11(4): 65-76. [4]KOJIC S,TRIFUNAC M D.Earthquake stresses in arch dams:I-theory and antiplane excitation[J].J Eng Mech,ASCE,1991,117(3):553-574. [5]LUCO I E.Dynamic interaction of a shear wall with the soil[J].J Eng Mech,ASCE,1969,95:333-346. [6]TRIFUNAC M D.Interaction of a shear wall with the soil for incident plane SH waves[J].Bull Seism Soe Am,1972,62:63-83. [7]TOTOROVSKA M I,TRIFUNAC M D.Analytical model for in-plane building-foundation-soil interaction:Incident P-SV-and Rayleigh Waves[R].los angeles,California:Dept of Civil Engrg,University of Southern California,1990:No.CE 90-01. [8]TOTOROVSKA M I,TRIFUNAC M D.The system damping,the system frequency and the system response peak amplitudes during in-plane buildingsoil interaction[J].Earthquake Engrg Struct Dynam,1992,21(2):127-144. [9]邱发强,刘殿魁.SH波入射时柔性基础上等腰三角形坝体结构的出平面反应[J].地震工程与工程振动,2006,26(4):9-17.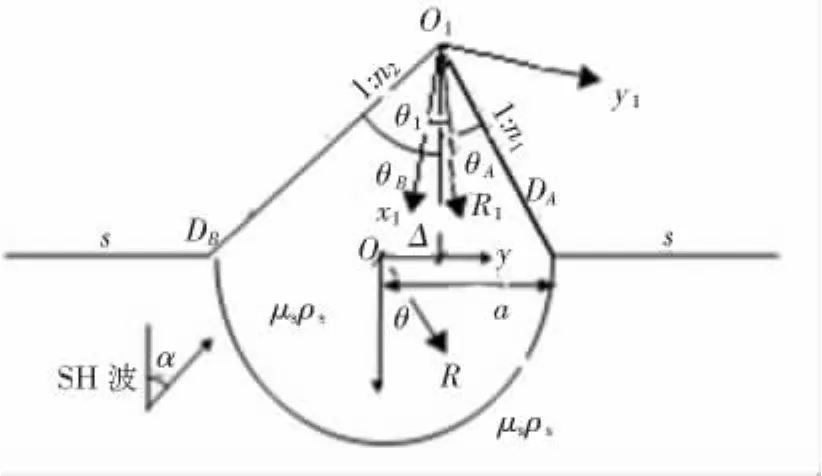
2 非等腰三角形区域内的驻波

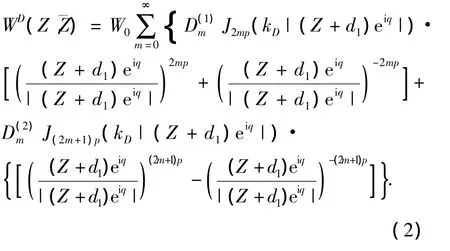


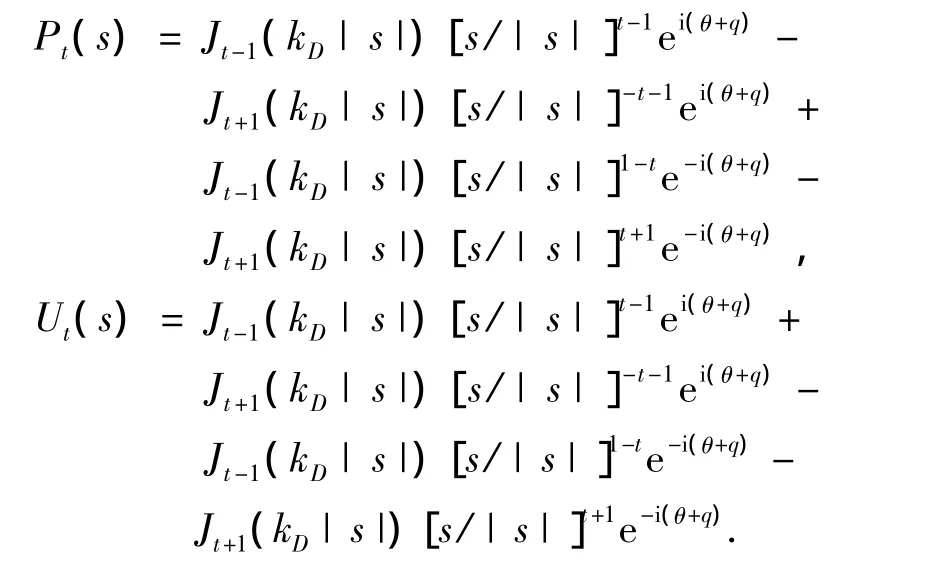
3 区域II内的波函数
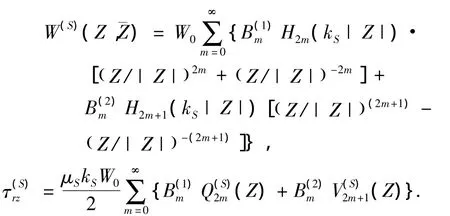



4 问题求解及定解方程组
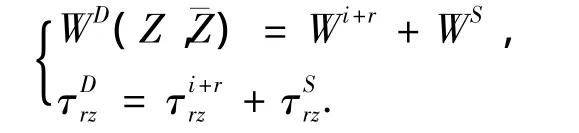

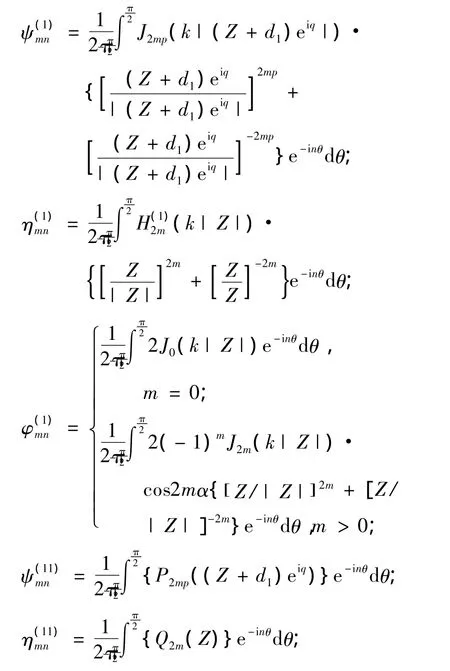
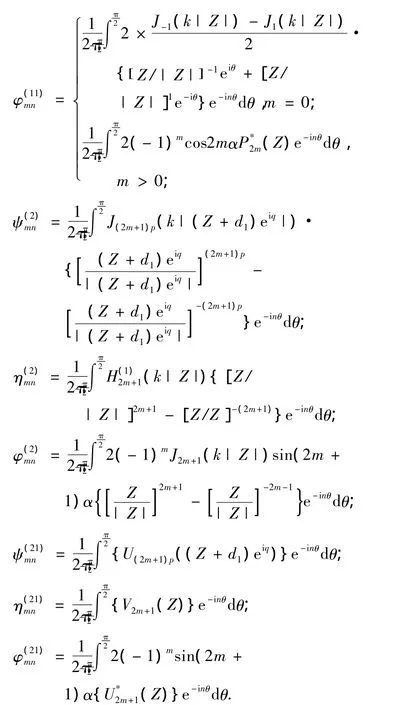
5 地面位移幅值
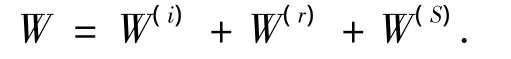
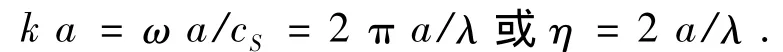
6 算例及结果分析

7 结论

