压力敏感性材料球形孔洞动态扩展问题
唐立强,于雪梅,2,吴国辉
(1.哈尔滨工程大学航天与建筑工程学院,哈尔滨150001,tlq8854@126.com; 2.中航工业哈尔滨飞机工业集团有限责任公司飞机设计所,哈尔滨150066)
压力敏感性材料在静水压力下存在塑性体积应变,其力学性能与金属材料有显著的不同.由于球形孔洞膨胀模型具有对称性、简便明确并易于给出应力和应变场解,从而揭示材料的变形本质,对压力敏感性材料中球形孔洞膨胀模型的深入研究已成为当前固体力学中的重要课题.自Taylor、Bishop、Hopkins等人在工程领域中做出了开创性的工作以来,根据岩土材料的变形机理,采用弹塑性力学[1-2]、损伤力学[3-4]、宏观 -细观力学理论[5],建立材料本构方程的工作从来没有停止过.最近,较为关注压力敏感性材料球形孔洞动态扩展的问题.由于研究的领域不同,根据具体情况抽象出不同的受压球形(柱形)孔洞膨胀模型,从而在理论上解决实际工程问题.对于岩石、金属、混凝土等材料的高速冲击试验和理论问题,Forrestal和Tzou研究了混凝土靶的侵彻问题[6],Satapathy研究了脆性陶瓷中球形孔洞的动态扩展问题[7],M.Mata等研究了在理想塑性和幂硬化材料中压痕试验的球孔扩展与锥头尺寸的关系[8];在孔洞的动态扩展方面,Durban和Masri研究了在可压缩弹塑性Mises和Tresca固体以及在压力敏感弹塑性介质中孔洞的动态膨胀问题[9].应指出的是,这些研究大多采用M-C屈服准则或D-P准则,而在球对称条件下,M-C屈服准则和DP准则具有相似的形式,即有效应力可以由Σr、Σθ线性表出,因此,减小了问题的复杂性.
本文首次采用椭圆型压力敏感性材料屈服准则和自相似假设,并结合三区模型,研究幂硬化材料球形孔洞动态扩展的问题.最后通过数值计算讨论了不同条件下材料参数对场量的影响.
1 孔洞动态扩展模型
在自相似假设下,考虑一个半径为A受内压P作用的球形孔洞的动态扩展问题,设内径扩展速度 ˙A为常数.问题模型如图1所示.其中ξ= r/A,A为空间的内半径,ξi为弹塑性交界,ξw为波前相对尺度参数.
边界条件为
当ξ=1时,

当ξ=ξi时,

当ξ=ξw时,
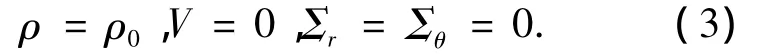
式中:下标e表示弹性区,p表示塑性区.

图1 球形孔洞动态膨胀场示意图
2 基本方程
2.1 几何方程
采用球形坐标(r,θ,φ)可以得到几何方程:
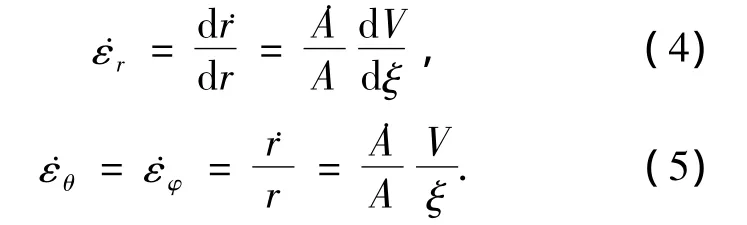
2.2 运动方程

式中:()′表示对ξ求导,ρ0为变形前的材料密度,为球形孔洞量纲一化的膨胀速度.
2.3 本构方程
采用椭圆形屈服条件和塑性势函数,分别为

式中:k1,k2为常数.α1,α2反映了材料的压力敏感性.当α1=α2时,材料是相关联的;而当α1= α2=0时,则退化为著名的Mises材料.
结合正交流动法则和材料的本构关系,可得幂硬化材料的本构方程为

Σe、Σ为定义等效应力和塑性势.在球对称条件下,有

显然,若材料是相关联材料时,Σe=Σ.
2.4 控制方程
将式(4)、(5)代入式(7),并化简有
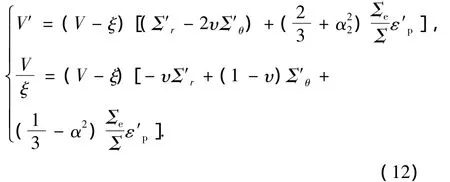

将式(12)带入式(13)并化简得

2.5 屈服条件
在塑性区,即当1≤ξ≤ξi时,材料满足屈服条件,即

其中,Σy为量纲一化的屈服应力(σs为屈服应力).
综上所述,式(6)、(12)、(14)即构成了幂硬化材料的控制方程组,其中变量有(Σθ,Σr,V,ρ),4个方程解4个未知数,方程是可解的.
3 弹性区的解
在弹性区,有εp=0,此时式(9)即化为弹性本构关系.考虑边界条件(1)~(3)以及在弹性区有|Σr|≪1,|Σθ|≪1,,则可求得弹性区的解为

4 幂硬化材料塑性区的解

其中:

方程(20)~(23)结合(16)、(17)确定的初始条件通过数值算法即可求出塑性区的场量分布.注意到当εp=0时,解(20)~(23)即化为弹性区的解.
5 数值计算
方程(16)、(17)中存在两个待定参数ξi和C2,在弹塑性边界,应力应满足屈服条件(15),即有
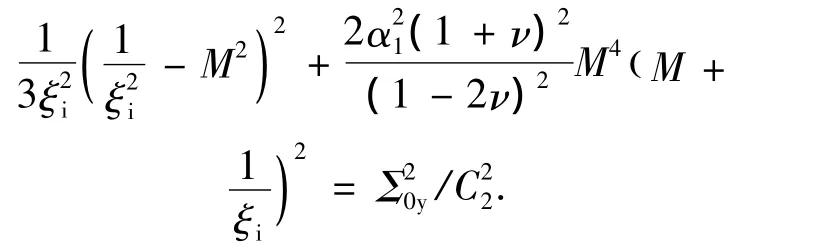
因此,参数ξi和C2是相关的.在计算中只需采用打靶法,给定任意的ξi≥1,,把计算的应力场带入式(21),直到在ξ=1处满足V=1为止.
对相关参数分别取不同值,通过数值计算确定各参数对场量的影响.
1)考察泊松比υ对场量的影响
当m=0.25,B=100,n=2,α1=0.25,α2=0.1,υ=0.15/0.35时,结果见图2.
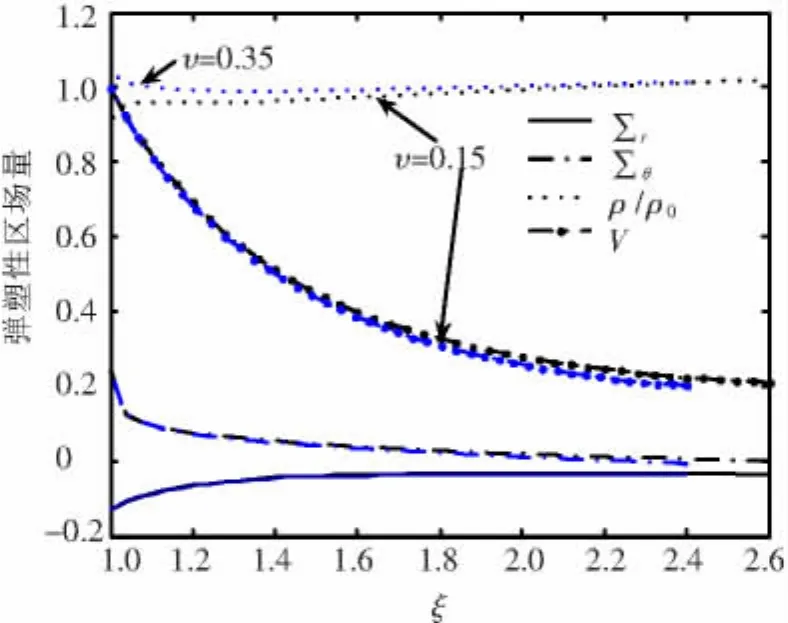
图2 不同泊松比υ对场量的影响
2)考察m对场量的影响
当υ=0.25,B=100,n=2,α1=0.25,α2= 0.1,m=0.15/0.35时,结果见图3.
3)若材料是相关联的,考察压力敏感性参数α1=α2对场量的影响

图3 不同孔洞膨胀速度m对场量的影响
当材料参数υ=0.25,B=100,n=2,m= 0.25,α=α=0/0.25时,结果见图4.

图4 相关联材料,不同α1=α2对场量的影响
4)若材料是非相关联的,考察参数α1,α2对场量的影响
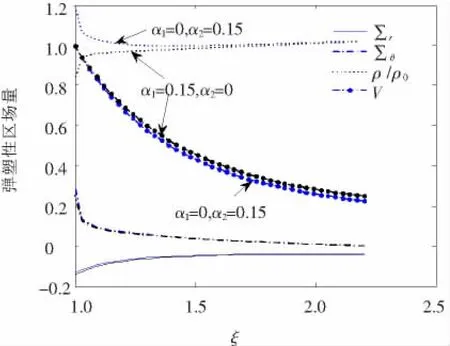
图5 非关联材料,α1,α2对场量的影响
6 结论
1)在塑性变形区内,应力和应变(绝对值)随着ξ的减小而增大,在内半径处达到极大值,满足球形孔洞膨胀特征.
2)在塑性变形区内,随着ξ的增大,V值减小,在弹塑性边界ξi处其与弹性区保持连续.
3)在塑性变形区内,ρ/ρ0的变化是复杂的.从方程(20)可以看出ρ/ρ0的变化不仅与α2相关,而且与泊松比ν相关.在ν较小时,弹性的体积变形大于塑性体积变形,出现ρ/ρ0≤1的现象,在ν=0.35时,在边界处ρ/ρ0≥1,说明在塑性变形区内有硬化现象的发生(见图2).
4)量纲一化的膨胀速度m对塑性区的大小有较大影响.在内半径处V保持常数,随着m的减小,塑性区的尺度增大.另外,m对塑性区的应力、速度、密度场均有影响(见图3).
5)关联参数α1,α2对应力场的影响很小,但影响ρ/ρ0的变化.当α21=0,α22=0.15时,在边界附近ρ/ρ0≥1;当α21=0.15,α22=0时,在边界附近ρ/ρ0≤1.因而关联参数α2影响ρ/ρ0的变化(见图4,5).
[1] MASRI R,DURBAN D.Quasi-static cylindrical cavity expansion in an elastoplastic compressible Mises solid[J].International Journal of Solids and Structures,2006,43:7518-7533.
[2] WU Guohui,WANG Yong,TANG Liqiang,et al. Cavity dynamic formation and bifurcation of the rubber—like sphere[J].Key Engineering Materials,2008,385/387:53-56.
[3] ZAIRI F,NAIT-ABDELAZIZ M,GLOAGUEN J M,et al.Modeling of the elasto-viscoplastic damage behavior of glassy polymers[J].International Journal of Plasticity,2008,24(6):945-965.
[4] 余寿文,冯西桥.损伤力学[M].北京:清华大学出版社,1997.
[5] 王自强,黄筑平.细观塑性理论[M].北京:科学出版社,1996.
[6] FORRESTAL M J,TZOU D Y.A spherical cavity expansion penetration model for concrete targets[J].International Journal of Plasticity,1998,14(1/3):173-191.
[7] MATA M,CASALS O,ALCALA J.The plastic zone size in indentation experiments:The ananlogy with the expansion of a spherical cavity[J].International Journal of Solid and Structures,2006,43:5994-6013.
[8] SATAPATHY S.Dynamic spherical cavity expansion in brittle ceramics[J].International Journal of Solids and Structures,2001,38(32/33):5833-5845.
[9] DURBAN D,MASRI R.Dynamic spherical cavity expansion in a pressure sensitive elastoplastic medium[J].International Journal of Solids and Structures,2004,41:5697-5716.

