一种深空自主导航系统可观测性分析方法
常晓华,崔平远,2,崔祜涛
(1.哈尔滨工业大学深空探测基础研究中心,哈尔滨150080,changxh1982@126.com; 2.北京理工大学宇航学院,北京100081)
对于深空自主导航系统,由于不能够直接测得探测器与中心天体或导航目标天体之间的距离,通常利用敏感器测量参考天体(太阳、恒星、行星及其卫星、小行星等)相对于探测器的方位信息[1],并结合状态估计算法,解算出探测器的位置和速度.然而,利用测量信息能否解算出探测器的轨道主要依赖于自主导航系统的可观测性.因此,判断自主导航系统能否满足任务要求的第一步,就是分析其可观测性.由于深空自主导航系统对应的状态方程和观测方程的非线性导致分析其可观测性存在一定的困难.传统的方法是将其线性化后离散化,然后利用线性离散系统的可观测性理论来分析导航系统的可观测性[2].Lee和Markus[3]论证了线性化系统可观测性与原系统局部一致.但是,一个可观测的连续系统,离散化后并不一定能保持其可观测性.刑光谦[4]针对离散线性系统,利用随机系统的可观测性矩阵定义了量测系统的可观测度,并建立了该可观测度与状态估计精度之间的解析关系; Fredric M.Ham[5]利用Kalman滤波的协方差阵定义可观测度,以协方差阵的特征值大小来衡量系该可观测性的强弱.
对于非线性系统,现有的可观测性分析方法主要分为以下三类:一类是将非线性系统线性化后得到系统的可观测矩阵,然后利用线性系统的可观测分析方法[6~8];一类是从非线性系统出发,分析系统的可观测性秩条件[9]和局部弱可观测[10]等;第三类是利用滤波算法产生仿真结果[5].这些方法只可以定性地分析系统是否可观测,或者判断某一时刻哪些状态或其线性组合是否可观测,并不能定量地给出系统在整个时间区间内的可观测度.
针对上述问题,本文结合微分几何的非线性系统理论,通过李导数求解非线性系统的可观测矩阵,并利用条件数给出了一种衡量系统可观测度的分析方法;将该方法应用于深空自主导航系统的可观测性分析,在建立太阳视线矢量观测模型的基础上,研究不同轨道参数对系统可观测性能的影响;结合扩展卡尔曼滤波建立自主导航算法,仿真分析不同可观测度条件下自主导航系统的状态估计精度.通过仿真结果验证提出的非线性系统可观测分析方法的可行性.
1 非线性系统的可观测性
考虑如下非线性系统

式中:状态矢量X∈Xn⊂Rn,观测矢量z∈Rm;状态方程f和观测方程h为C∞内光滑的解析函数.
由微分几何理论可知[10],h沿f的各阶李导数为


进而,可以得到研究非线性系统可观测性的一个常用工具,即观测空间.系统Σ的观测空间H是由生成的线性空间,该空间按如下方式定义了Σ的可观测性分布:

对X0∈Xn,如果dim dH(X0)=n,则称系统Σ在X0点满足可观测性秩条件.若对∀X∈Xn,Σ都满足可观测性秩条件,则称系统Σ满足可观测性秩条件[10].
由dHn定义的非线性系统的可观测矩阵Q(X)可以表示为

局部弱可观测性在数学上强调了状态的局部可区分性,而在实际中需要确定的状态对象往往是带有局部区域限制的,因此,在可观测性分析中强调局部这个限制并无必要[12].系统的可观测性只能说明系统的状态是否能够从观测量来确定,而无法反映估计性能的好坏.为描述系统状态估计的精度,需要进一步研究系统的可观测度.
在矩阵理论中条件数定义为

式中:σmax和σmin分别为矩阵的最大奇异值和最小奇异值.可见,矩阵的条件数是一个大于或等于1的正数,条件数越大,说明矩阵越接近于病态.因此,利用矩阵的条件数可分析系统的可观测度.
基于上述分析,利用可观测矩阵Q(X)的条件数定义的非线性系统的可观测度为

由可观测度的定义可知,对X0∈Xn有0≤δ(X)≤1;当δ(X)>0时有rank(Q(X))=n,即系统Σ是局部弱可观测的;当δ(X)=0时有rank(Q(X))<n,即系统Σ不是局部弱可观测的,当然也就不是可观测的.可见,可观测度的定义中还蕴含着系统是否可观测条件.
由上述分析知,可观测度依赖于系统的状态模型和观测模型,与观测数据本身无关,故可作为比较观测模型好坏的一个性能准则.显然,在应用中应选择可观测度高的观测模型,以便获得高精度的状态变量估计值.
2 深空自主导航系统的可观测性
2.1 自主导航系统建模
在日心惯性坐标系下,深空探测器的轨道动力学模型为

式中:r=[x, y, z]T和分别为探测器的位置和速度,且r=‖r‖;μ为太阳引力常数;a为行星引力、太阳光压等未建模的摄动加速度矢量.
选取状态变量X=[rT, vT]T,根据轨道动力学模型得到探测器的状态方程为

式中:w为系统模型误差.
在深空探测任务中,可用于矢量观测的参考天体主要有太阳、大行星及其卫星和已知星历的小行星等,其中太阳是最稳定也是最重要的参考天体,能提供丰富的光谱信息和电磁信号,直接将太阳信息作为观测量能够简化导航系统的信息处理过程[13].太阳视线矢量的观测模型如图1所示.

图1 太阳视线矢量观测模型
图1中,r为探测器在日心惯性坐标系下的位置矢量,l为系统观测的太阳视线矢量.太阳视线矢量的观测模型为
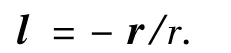
考虑到视线矢量的观测误差,可得太阳矢量的观测方程为

式中:v为系统观测噪声,假设为零均值高斯白噪声.
2.2 自主导航系统的可观测性
取深空探测器相对日心黄道惯性坐标系的轨道参数为半长轴a=2×108km,偏心率e=0.25,轨道倾角i=23°,升交点赤经Ω=1.16°,近日点幅角w=108.89°,初始时刻真近角f=0°.
在计算过程中,由于轨道参数和观测量选取不同的单位,会导致可观测矩阵不同元素在数值上有很大的不同,从而无法正确分析导航系统的可观测性,因此需要对轨道参数和观测量进行无量纲化处理.
对于以太阳为中心天体的深空轨道,相应的距离单位[L]、速度单位[V]和时间单位[T]分别取为

式中:μs为太阳引力常数.
无量纲化后的状态变量为

进而,利用X'可直接得到无量纲化的观测量.
1)深空自主导航系统的可观测度.图2给出了可观测度曲线.从图中可以看出,在近日点导航系统的可观测度较低,而在远日点可观测度较高.这是由于探测器在近日点飞行速度高,在飞越相同的空间距离过程中,飞行时间短,其观测次数少,故可观测度较低;而在远日点飞行速度低,在飞越相同空间距离的过程中,飞行时间长,其观测次数多,故可观测度较高.可见,对于同一量测系统,使用的测量数据越多,可观测度越高,与参考文献[4]中的结论一致.

图2 深空自主导航系统可观测度曲线
2)半长轴对导航系统可观测性的影响.在偏心率(e=0.25)和轨道倾角(i=23°)保持不变的前提下,图3给出了半长轴a从1×108km到9×108km变化过程中导航系统可观测度的变化曲线,半长轴的变化步长为1×107km.

图3 半长轴对导航系统可观测性的影响
从图中可以看出,对于以太阳视线矢量为观测量的导航系统中,轨道半长轴对系统可观测度的影响比较明显.当半长轴较小时,导航系统在近日点可观测度较低,在远日点可观测度较高;而当半长轴较大时,导航系统在近日点可观测度较高,在远日点可观测较低.
3)轨道倾角对导航系统可观测性的影响.在半长轴(a=2×108km)和偏心率(e=0.25)保持不变的前提下,图4给出了轨道倾角 i从0°~100°变化过程中导航系统可观测度的变化曲线,轨道倾角的变化步长为10°.

图4 轨道倾角对导航系统可观测性的影响
从图中可以看出,轨道倾角对基于太阳视线矢量的导航系统的可观测度的影响并不明显.这是因为轨道倾角只是改变探测器飞行轨道面在惯性空间的指向,而并不影响轨道速度和对太阳视线矢量的观测.
4)偏心率对导航系统可观测性的影响.在半长轴(a=2×108km)和轨道倾角(i=23°)保持不变的前提下,图5给出了偏心率e从0.1~0.9变化过程中导航系统可观测度的变化曲线,偏心率的变化步长为0.1.

图5 偏心率对导航系统可观测性的影响
从图5中可以看出,偏心率的变化对以太阳视线矢量为观测量的导航系统的可观测度的影响比较复杂.为深入分析偏心率对系统可观测度的影响,图6给出了不同偏心率下系统的可观测度在二维坐标系内的变化曲线.

图6 偏心率对导航系统可观测性的影响
从图6可以看出,当0<e<0.6时,基于太阳视线矢量的导航系统在近日点可观测度较低,在远日点可观测度较高;而当0.6≤e<1时,系统的可观测度变化曲线不再是简单的近正弦曲线,而是在远日点的可观测度有所下降,并出现低于相邻位置可观测度的现象.其原因在于,对于偏心率较大的椭圆轨道,探测器在远日点附近时,相邻几次对太阳视线矢量的观测容易产生视线重叠现象,即观测到的太阳视线矢量不可分辨,从而使得远日点的可观测度较低.
通过详细分析轨道参数对基于太阳视线矢量的深空自主导航系统可观测性的影响可知,文中提出的利用非线性系统可观测矩阵的条件数定义的可观测度的方法是可行的,能够直观地反映出不同圆锥轨迹下导航系统可观测性能的变化.在具体的深空探测任务实施中,应选择可观测度高的观测模型,以获得高精度的轨道参数估计结果.
3 仿真分析
为进一步验证导航系统可观测度与状态估计精度之间的关系,结合非线性扩展卡尔曼滤波(EKF)算法,以太阳视线矢量为观测量,对不同可观测度条件下的自主导航系统进行仿真分析.
基于太阳视线矢量的自主导航系统的状态方程如式(1)所示,观测方程如式(2)所示,基于EKF自主导航算法的具体过程见参考文献[14].在仿真分析中,以导航系统可观测性分析的轨道参数作为标称轨道,详细仿真条件如下.
1)标称轨道参数:半长轴a=2×108km,偏心率e=0.25,轨道倾角i=23°,升交点赤经Ω=1.16°,近日点幅角w=108.89°,初始时刻真近角f=104.48°;
2)初始位置误差为6×105km,速度误差为0.05 km/s;系统模型误差阵为Q=1×10-15·I6×6;
3)太阳视线矢量测量误差为5×10-5rad;
4)采样时间间隔为1 800 s,仿真时间为1.8×107s.
由自主导航系统的可观测性分析结果可知,初始轨道参数反向积分对应于可观测度较低的系统(系统一),正向积分对应于可观测度较高的系统(系统二).在上述仿真条件下,图7~10分别给出了两种可观测度情况下导航系统的位置和速度估计误差曲线,表1列出了仿真结束时刻的位置和速度估计误差.

图7 位置估计误差曲线(系统一)

图8 速度估计误差曲线(系统一)

图9 位置估计误差曲线(系统二)

图10 速度估计误差曲线(系统二)

表1 最终位置和速度估计误差
从仿真结果可以看出,对于可观测度较低的系统一,其导航滤波过程收敛较慢,最终位置估计误差在450 km以内,速度估计误差在7.5×10-5km/s以内;对于可观测度较高的系统二,其导航滤波过程收敛较快,且最终位置估计误差在147 km以内,速度估计误差在2.9×10-5km/s以内.
可见,导航系统可观测度的高低直接反映了观测模型对状态的估计性能,在应用中应选择可观测度高的观测模型,甚至融合不同类型的观测信息,以获得高精度的状态估计值.有关可观测性的研究,能够为系统状态估计选择更合适的观测模型提供理论依据.
4 结论
从仿真结果可以看出,文中提出的可观测性分析方法能够直观地反映出不同圆锥轨迹下深空自主导航系统可观测性能的变化,相关结果和分析方法可为导航系统观测模型的选取提供参考.
[1]胡小平.自主导航理论与应用[M].长沙:国防科技大学出版社,2002:18-24.
[2]宁晓琳,房建成.航天器自主天文导航系统的可观测性及可观测度分析[J].北京航空航天大学学报,2005,31(6):673-677.
[3]LEE E B,MARKUS L.Foundations of Optimal Control Theory[M].New York:John Wiley,1967.
[4]邢光谦.量测系统的能观度和状态估计精度[J].自动化学报,1985,11(2):152-158.
[5]HAM F M,BROWN R G.Observability,eigenvalues and Kalman Filtering[J].IEEE Transaction on Aerospace and Electronic Systems,1983,19(2):269-273.
[6]GOSHEN M D,BAR I I Y.Observability analysis of piece-wise constant system[J].IEEE Transaction on aerospace and electronic system,1992,28(4):1025-1075.
[7]范炜,李勇.基于奇异值分解的航天器自主导航系统能观度分析[J].航天控制,2009,27(2):50-55.
[8]CHEN Zhen.Local observability and its application to multiple measurement estimation[J].IEEE Transactions on Industrial Electronics,1991,38(6):491-496.
[9].黄翔宇,崔平远,崔祜涛.深空自主导航系统的可观性分析[J].宇航学报,2006,27(3):332-337.
[10]ROBERT H,ARTHUR J K.Nonlinear control and observability[J].IEEE Transactions on Automatic Control,1977,22(5):728-740.
[11]GAUTHIER J P,BORNARD G.Observability for Any u(t)of A Class of Nonlinear Systems[J].IEEE Transactions on Automatic Control,1981,26(4):922-926.
[12]SONTAG E D.A concept of local observability.Systems&Control Letters,1984,5(1)41-47.
[13]GUO Y P.Self-contained autonomous navigation system for deep space missions[J].Advances in the Astronautical Sciences,1999,102(2):1099-1113.
[14]付梦印,邓志红.Kalman滤波理论及其在导航系统中的应用[M].北京:科学出版社,2003:46-48.
[15]CRASSIDIS J L,ALONSO R,JUNKINS J L.Optimal attitude and position determination from line of sight measurements[J].The Journal of the Astronautical Sciences,2000,40(2):391-408.

