多肋式梁桥在全过程中应力重分布研究

张 剑，黄剑峰，叶见曙，俞 博

(1.南京航空航天大学结构工程与力学系，南京210016，jianzhang78@126.com;2.云南农业大学水利水电与建筑学院，昆明650201;3.东南大学桥梁工程研究所，南京210096)

多肋式梁在实际工程中有着广泛的应用，其在荷载作用下的结构响应一直为工程界关心［1－2］.目前，用三维弹性有限元分析多肋式梁的线弹性行为是容易的，已有多种商业有限元软件能够完成.但对于多肋式梁的非线性分析而言，特别是对于预应力混凝土多肋式梁结构，由于预应力效应准确模拟的困难以及三维非线性有限元分析程序编制的复杂性，迄今为止这方面的研究成果出现甚少，大部分研究成果集中在单梁的非线性:如文献［3］考虑了塑性铰长度，采用具有假定弯矩－曲率关系的梁单元分析了预应力混凝土T梁结构行为;文献［4］采用分层梁单元对T梁结构行为进行了非线性分析;文献［5］应用分层壳单元方法进行了Leonhard钢筋混凝土深梁的非线性全过程分析;文献［6］采用梁单元模拟T梁的梁肋，采用分层板单元模拟T梁的翼缘板进行了分析;文献［7］采用带刚臂的3节点Timoshenko梁单元模拟T梁的梁肋，采用8节点的Mindlin单元模拟T梁的翼缘板.还有用ANSYS中较受青睐的Solid65单元来进行梁、柱等简单结构的非线性分析［8－10］，但由于Solid65单元的非线性计算稳定性和收敛性较差［11］，难以用于预应力混凝土多肋式梁和箱梁等较为复杂结构的非线性分析，目前也没有这方面的研究文献报道.

由于破坏试验本身的难度较大，其规模和限制影响因素之多是室内试验所无法比拟的.迄今为止，国内外进行多肋式梁破坏试验的文献资料较为少见.借助于仅有宝贵的工程结构破坏试验数据，寻求可靠的计算理论来研究多肋式梁成为重要途径［12］.因此，研究多肋式梁非线性行为的计算方法、编制相应的计算程序是具有理论价值和实际工程意义的.本文着重研究预应力钢筋对组合壳单元刚度矩阵的贡献和统一的非线性壳单元模式，并研究工程薄壁多肋式梁的破坏全过程分析方法和应力重分布规律.

1 非线性单元模式的研究

1.1 实体退化壳单元

体单元及相应的退化壳元如图1和图2所示.图1中体单元的控制节点18个，退化壳元的控制节点9个，用于描述退化壳元的信息明显减少［13］.且假设:退化壳元的垂直于中面的法线在变形后仍为直线，且垂直于壳中面的应力分量假设为零.

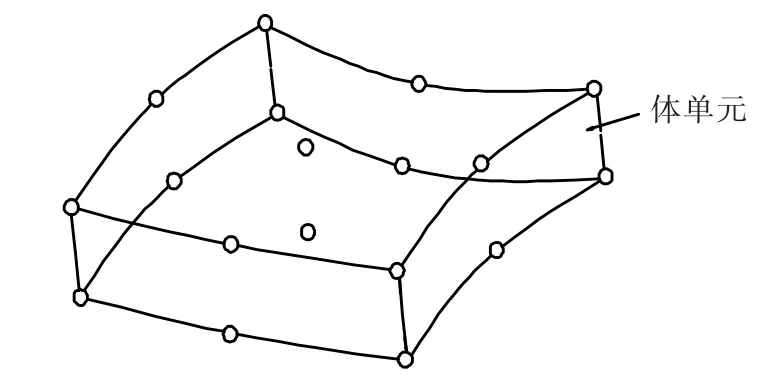
图1 体单元描述

预应力混凝土多肋式梁由混凝土、普通钢筋和预应力钢筋组成，其材料性能和应力是ζ的不连续函数.而混凝土的屈服、开裂等结构行为需用到沿壳厚方向的积分来表达.分层法简洁而有效地解决了此问题，将不连续函数的积分问题化为有限项级数求和问题，且能保证工程精度.沿ζ方向的分层模型如图3所示.

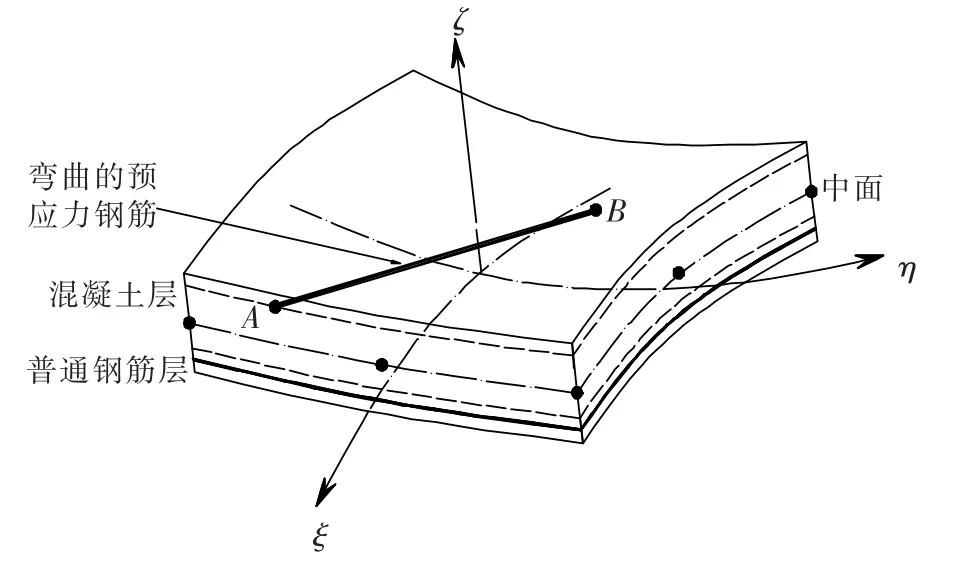
图2 退化壳单元描述

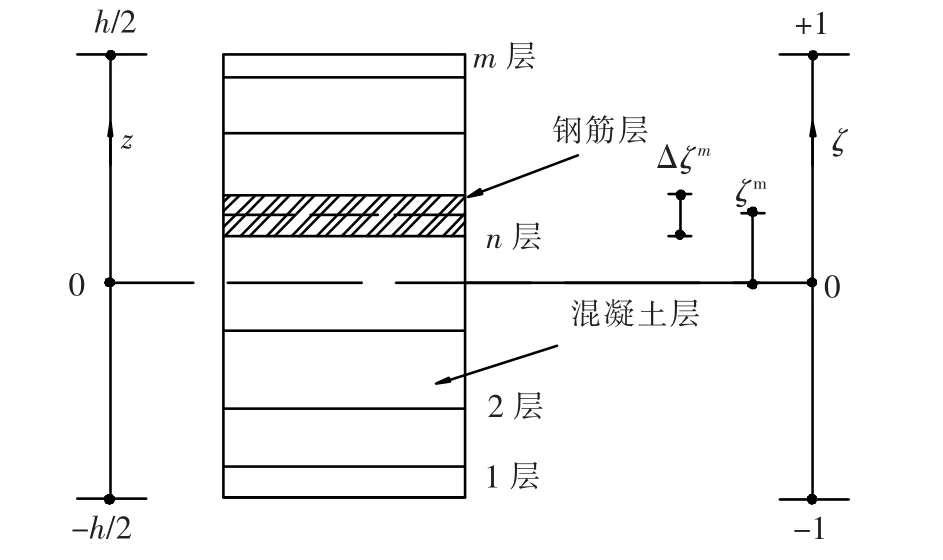
图3 壳元分层模型

2.2 组合壳单元

对于弯曲的预应力钢筋，用层单元等模拟过于近似，本文研究用组合壳元模拟.组合壳元中预应力钢筋单元起点A和终点B如图2所示，利用实体退化壳单元位移插值公式［13］，则钢筋单元的节点位移可用壳元节点位移表示为

式中:n为壳元节点数，hi为节点i处壳元厚度，为节点i的节点坐标系ν与x轴夹角余弦值，其1余类推、分别为形函数Ni在节点A和节点B的值;ζA、ζB分别为预应力筋起点A和终点B的ζ向局部坐标，δi为壳元的节点位移列阵，Ri为转换矩阵.并记，则式(1)可写为:δS=RδC.

则应用虚功原理［14］，推得预应力钢筋单元对组合壳元刚度矩阵的贡献:

式中:KP为预应力钢筋对组合壳元刚度矩阵的贡献;KS为整体坐标系下预应力钢筋单元刚度矩阵.

混凝土和普通钢筋采用分层壳单元模拟，预应力钢筋采用组合壳单元模拟，则统一的非线性壳单元刚度矩阵推导为

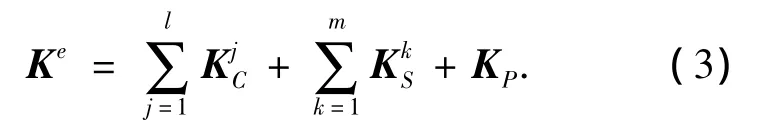
式中:l、m分别为非线性壳单元中混凝土和普通钢筋的层数，Ke为非线性壳单元刚度矩阵，KjC为壳元中第j层混凝土层的刚度矩阵为壳元中第k层普通钢筋层的刚度矩阵和均可利用高斯求积公式计算.KP为式(3)的预应力钢筋对非线性壳元刚度矩阵的贡献.

2 非线性力学性能描述

2.1 混凝土屈服准则

由于壳元需考虑横向剪切作用，本文选择Owen双参数三轴屈服准则，表达式为

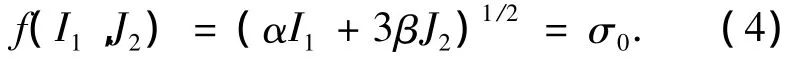
式中:I1为应力张量第一不变量;J2为应力偏量第二不变量;σ0为等效应力，取为单轴抗压强度fc; α、β为材料参数，由式(4)根据单轴抗压试验和双轴等压试验标定

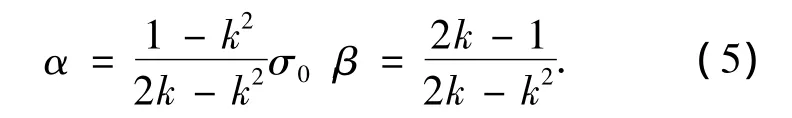
2.2 混凝土强化准则

强化准则确定了塑性变形过程中后继屈服面(加载表面)的运动.它决定了加载面以及累计塑性应变之间的关系.利用有效应力和有效塑性应变的物理意义，使得混凝土力学行为的描述可用单轴试验来外推得到多轴时的情况.弹塑性矩阵中的强化参数H'可由有效应力σ对有效塑性应变εp的斜率表示，即

Madrid线型的单轴有效应力σ和有效塑性应变εp关系式为

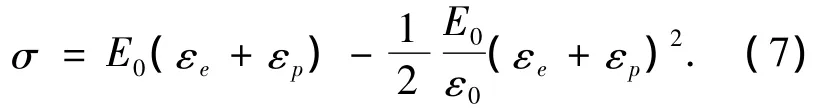
式中:E0为初始弹性模量;ε0为单轴抗压强度fc时的总应变，可取为为弹性应变，即为

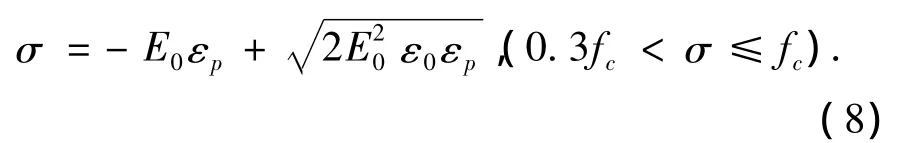
式中:强化参数H'即可由式(6)和式(8)求出.

2.3 混凝土压碎准则

混凝土的压碎断裂由应变控制，Hinton压碎准则表达式为

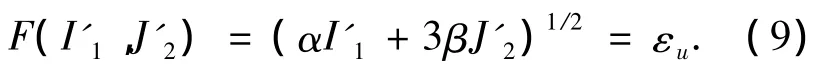
式中:I'1为应变张量第一不变量;J'2为应变偏量第二不变量;εu为混凝土极限压应变.

2.4 钢筋材料非线性特性

预应力混凝土多肋式梁的钢筋材料分为普通钢筋和预应力钢筋.普通钢筋采用壳元中等效厚度的层单元考虑［13］.假定每一钢筋层的力学性能是单向的，只能承受沿钢筋方向的轴向力.本文预应力钢筋采用组合壳单元考虑.采用双折线强化弹塑性模型模拟钢筋的本构关系［15］.

单轴有效应力σ和有效塑性应变εp的关系式为

3 非线性分析的收敛准则

在预应力混凝土多肋式梁的非线性分析中，由于考虑了钢筋混凝土材料非线性效应，涉及到大型非线性有限元方程组的求解问题，本文采用增量－迭代法求解.现有的迭代方法分为:直接迭代法、切线刚度法、割线刚度法和等刚度法等.等刚度法只需一次形成土多T梁分层壳整体刚度矩阵，其后无需重新生成整体刚度矩阵，在一定程度上节省了计算时间，提高了计算效率.本文综合采用等刚度法和切线刚度法，即在各增量步的第一次迭代时采用切线刚度法，各增量步内的其余迭代计算采用等刚度法.

收敛准则一般分为:力收敛准则和位移收敛准则.在预应力混凝土多T梁桥的非线性分析中，不平衡力常可形成一些平衡力系，使得解不能单调收敛，故本文采用位移收敛准则，取

式中:δi为第i增量步的非线性方程组迭代时的收敛解，即预应力混凝土多肋式梁第i增量步整体位移向量;δi+1为第i+1增量步的非线性方程组迭代时的收敛解;ε为收敛容差，取为2.5%.

4 非线性全过程分析

4.1 试验资料

文献［12］进行了沪宁高速公路上一预应力混凝土多肋式梁的破坏性试验研究，这在国内尚属首次.该多肋式梁桥由6片单梁组成，单梁截面如图4所示，并沿纵向设有5道横隔板(2道端横隔板，3道中横隔板).单梁长20 m，翼板宽2.08 m，梁高 1.4 m，腹板宽 0.18 m，马蹄宽0.40 m.桥梁所用材料为50号混凝土和强度级别为1 600 MPa高强钢丝.桥梁采用在现场整体拼装式大型钢模板预制施工，孔道采用金属波纹管成型，6根预应力钢束，控制张拉应力1 200 MPa，有效张拉应力1 000 MPa.桥梁支座采用板式橡胶支座，普通钢筋和预应力钢筋的详细布置见文献［12］.考虑到实桥破坏性试验加载量巨大，试验采用钢材加载方案，以确保试验顺利进行.同时为提高加载效率，文献［12］采用图5所示(G1表示第一片单梁肋中心所在位置，其余类推)的偏载加载方式，主梁G1所受均布荷载为主梁G2至主梁G5的2倍，主梁G6近似不受荷载作用，即通过钢材偏向桥面一侧来实现.

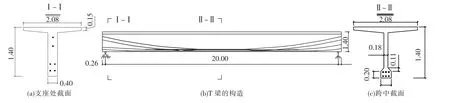
图4 预应力混凝土单T梁的截面图(m)

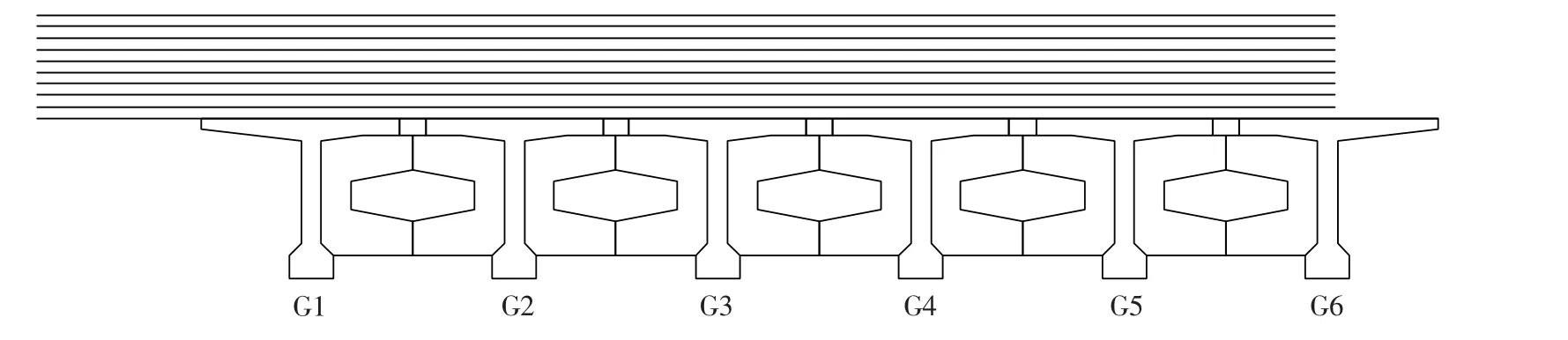
图5 钢材沿桥面横向布置

4.2 预应力混凝土多肋式梁的组合壳单元建模

预应力混凝土多肋式梁是典型的工程薄壁结构，采用壳单元模拟是适合的.梁体(主梁和横隔板)共划分成715个单元，2 739个节点，其中组合壳单元180个，有限元模型如图6所示.有限元计算加载方式采用文献［14］的加载方案，每级每20 m加载49.6 t的均布荷载.横向加载时，加载点为T梁肋板和顶板的交点处.

4.3 挠度计算结果

应用本文编制的三维非线性有限元程序，在各级荷载作用下，预应力混凝土多肋式梁的偏载端主梁G1的1/4跨、跨中和3/4跨梁底的挠度计算结果与破坏性试验资料的比较如图7所示.

从荷载－挠度曲线图7可知，用非线性有限元程序得到的计算值和试验值趋势相同，两者数据吻合程度良好，这说明了本文采用的实体退化壳单元、钢筋混凝土材料非线性描述以及预应力钢筋的组合壳单元模拟等用于预应力混凝土多肋式梁非线性分析的有效性和可靠性.破坏性试验得到多肋式梁极限承载力约为1 139.37 t，有限元得到多肋式梁极限承载力约为1 240.00 t，相对误差约为8.82%.

提取各主梁跨中截面梁底的挠度数据，可得相应的荷载－挠度曲线如图8所示.随着加载量增加，各主梁截面会出现刚度折减现象.由于加载偏载于主梁G1，在各级荷载作用下，主梁G1挠度最大，挠度发展最迅速，主梁G2至主梁G5挠度依次减小，主梁G6挠度变化不明显.

4.4 预应力钢筋应力发展

各主梁1/4跨和跨中截面梁底的预应力钢筋应力发展规律如图9，跨中处钢筋应力的相应数据见表1.

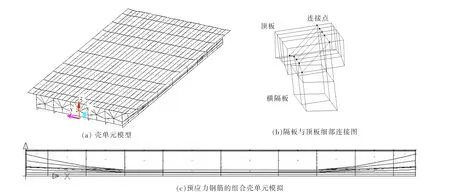
图6 预应力混凝土多肋式梁有限元模型

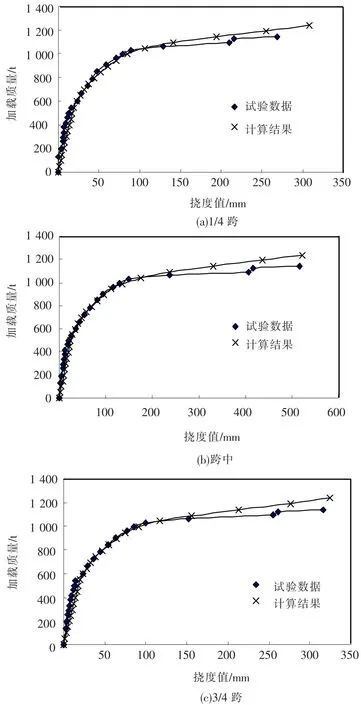
图7 挠度计算结果

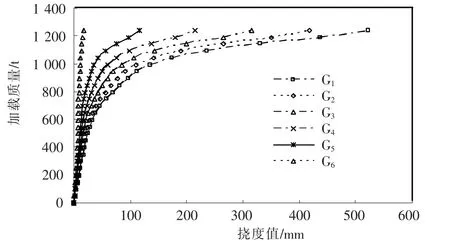
图8 各主梁跨中荷载－挠度曲线

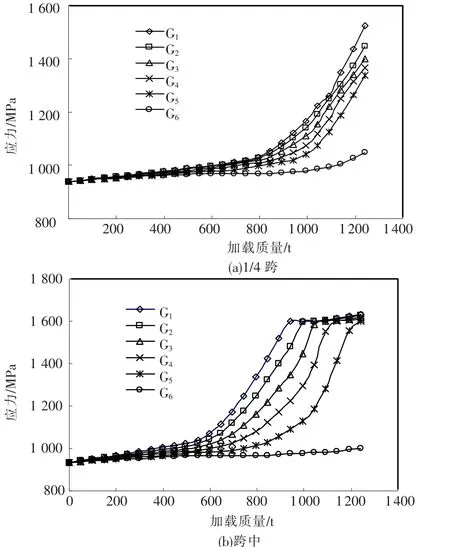
图9 各主梁预应力钢筋应力

由图9(a)可知，随着加载量增加，1/4跨截面各主梁的预应力钢筋应力都有增加，但在整个非线性过程中预应力钢筋均未发生屈服.由图9(b)和表1可以看出，随着加载量增加，跨中截面主梁G6的预应力钢筋应力变化幅度不大，其余各主梁的预应力钢筋应力都呈现明显的增大趋势.由于偏载作用，主梁G1的预应力钢筋应力增长速度最快，在加载第19级时，主梁G1的预应力钢筋首先屈服;继续加载，主梁G2至主梁G5的预应力钢筋应力也相继屈服，直至整个结构破坏.

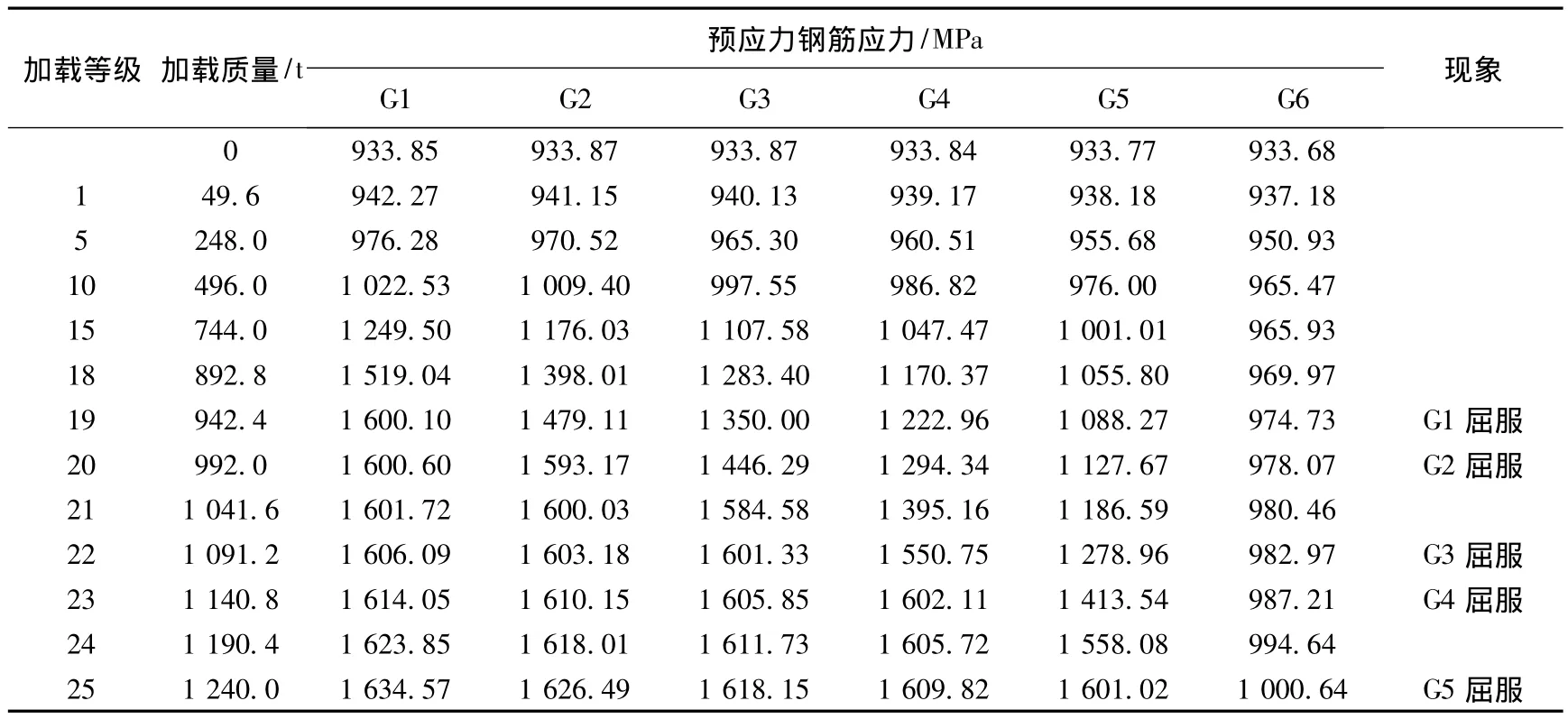
表1 各主梁跨中截面梁底的预应力钢筋应力

5 结论

1)用实体退化壳单元模拟预应力混凝土多肋式梁是适合的，单元用于非线性分析时表现出良好的数值稳定性和收敛性，计算精度较高.

2)预应力效应的准确模拟是重要的，采用组合壳单元模拟预应力钢筋及其非线性效应是有效的，这也是对一般用层单元等模拟预应力钢筋的一种改进.

3)编制预应力混凝土多肋式梁非线性全过程分析程序，计算结果包含大量的有用信息，对典型截面挠度和预应力钢筋应力发展规律进行了统计分析.该方法也有望在箱梁等结构的非线性分析中得到应用.

［1］SONG H W，YOU D W，BYUN K J，et al.Finite element failure analysis of reinforced concrete T-girder bridges［J］.Engineering Structures，2002，24(2):151－162.

［2］张剑，叶见曙.钢筋混凝土多T梁结构的分层壳元计算法［J］.水利学报，2006，37(11):1372－1377.

［3］LIN Z D，MICHEL G，A，JOAN R C.Nonlinear flexural behavior of prestressed concrete girder bridges［J］.Journal of Bridge Engineering，2001，6(4):276－284.

［4］FRAGIACOMO M，AMADIO C，MACORINI L.Finiteelement model for collapse and long-term analysis of steel-concrete composite beams［J］.Journal of Structural Engineering，2004，130(3):489－497.

［5］方自虎，孙璨.钢筋混凝土结构的三维有限元非线性分析［J］.计算力学学报，2006，23(3):377－380.

［6］WENDEL M S，RICHARD E M.Nonlinear FE analysis of steel-concrete composite structures［J］.Journal of Structural Engineering，2000，126(6):662－674.

［7］WONSEOK C，ELISA D S.Nonlinear finite-element analysis of composite steel girder bridges［J］.Journal of Structural Engineering，2005，131(2):304－313.

［8］SANTHAKUMAR R，CHANDRASEKARAN E，DHANARAJ R.Analysis of retrofitted reinforced concrete shear beams using carbon fiber composites［J］.Electronic Journal of Structural Engineering，2004(4):66－74.

［9］梅力彪，周云，阴毅.穿心暗牛腿钢管混凝土柱单梁节点空间非线性有限元分析［J］.工业建筑，2004，34(9): 81－83.

［10］QUEIROZ F D，VELLASCO P C，NETHERCOT D A.Finite element modelling of composite beams with full and partial shear connection［J］.Journal of Constructional Steel Research，2007，63(4):505－521.

［11］司炳君，孙治国，艾庆华.Solid65单元在混凝土结构有限元分析中的应用［J］.工业建筑，2007，37(1):87－92.

［12］张宇峰.沪宁高速公路扩建工程桥梁极限状态实桥试验研究试验［R］.南京:江苏省交通科学研究院，2006.

［13］HINTON E，OWEN D R J.Finite element software for plates and shells［M］.Swansea:UK Pineridge Press Ltd，1984.

［14］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京:清华大学出版社，2005.

［15］吕西林，金国芳，吴晓涵.钢筋混凝土结构非线性有限元理论与应用［M］.上海:同济大学出版社，1999.