楔形翼缘连接板腹板连接节点断裂性能

刘洪波，赵文军，李 爽，邵永松，谢礼立

(1.黑龙江大学建筑工程学院，哈尔滨150080，Interdage@163.com;2.哈尔滨工业大学土木工程学院，哈尔滨150090)

1994年1月17日发生在美国的北岭地震和正好一年后1995年1月17日发生在日本的阪神地震是两次陆域型强震.被认为抗震性能卓越的现代钢框架结构遭受了严重的破坏，而且梁柱节点的破坏主要发生在梁柱焊接接头处，且多为脆性破坏.美国北岭地震中，焊接钢框架节点的破坏，主要发生在梁的下翼缘，最典型的破坏形式是焊缝沿柱翼缘表面部分或完全断裂［1－2］，这种裂缝数量是其他所有破坏类型总数的二倍.

这种破坏形式既出现在工字钢梁与H型钢柱翼缘连接节点上，也出现在工字钢梁与H型钢柱腹板连接节点上［3］.国内外学者对工字钢梁与H型钢柱翼缘连接节点焊缝的断裂性能研究较多［4－6］，但对腹板连接节点焊缝的断裂性能研究较少［7］.

对于工字钢梁与H型钢柱腹板连接节点，通常延长翼缘连接板以便使其与梁冀缘的对接焊缝远离与柱冀缘的焊缝，从而避免了交叉焊缝与复合残余应力.我国的《高层民用建筑钢结构技术规程》(JGJ99－98)规定梁的翼缘连接板宜采用楔形，且伸出柱外约100落mm，以免该板在与梁翼缘的连接处因板件宽度突变而破裂.本文采用断裂力学与有限元分析相结合的方法，研究楔形翼缘连接板腹板连接节点焊缝的应力强度因子与构件尺寸之间的关系，并与仅延长翼缘连接板腹板连接节点进行了比较，从而为钢框架结构腹板连接节点抗震设计提供依据.本文判断焊缝开裂的依据是I型应力强度因子KI，KI可以通过J积分的方法求得.

1 有限元模型建立

美国Lehigh大学对最常用的梁柱腹板连接形式进行了足尺的单调加载试验［8－9］.在文献中对试件的制作、梁柱材性、焊缝材性及施焊顺序、螺栓型号及预拉力、加载方案及全部试验结果进行了详细介绍，可以获得比较齐全的试验数据，所提供的数据能够满足有限元模型验证的需要.

试验中的试件是根据美国钢结构设计规范设计的，梁柱分别采用W27×94，W14×246宽翼缘工字钢，梁长1.422 m，柱高5.5 m.螺栓直径22 mm，共5个.试验时在梁端施加一递增的单向荷载.梁、柱、翼缘连接板以及腹板连接板均采用ASTM A572钢，焊缝材料为E70型，螺栓采用ASTM A490高强螺栓.材料性能见表1.试验方案见图1.

表1 构件材料属性

本文建立的试验腹板连接节点的有限元模型见图2.有限元模型采用ANSYS中实体单元建模，除焊缝、缺陷和不规则形状处采用Solid95单元，其余全部采用Solid45单元.考虑剪切板和梁腹板之间的接触、螺帽与剪切板之间的接触、螺帽与梁腹板间的接触，采用目标单元TARGE170和接触单元CONTA173来模拟，摩擦系数取0.4.对于高强螺栓中的预拉力采用PRETS179单元进行模拟，每个螺栓施加218 kN的预拉力.

图1 试验方案

图2 试验腹板连接有限元模型

本文的有限元计算结果与试验结果的比较见图3，可以看出，在弹性阶段，有限元计算结果与试验结果非常接近，但试件屈服以后有限元计算的承载力略低于试验结果，这主要是由于计算模型中的材料与实际材料的本构关系之间存在差异，尤其是强化阶段，本文模型中采用的是多线性随动强化模型，与实际情况肯定存在一定差异.但总体而言，本文的计算结果与试验结果还是吻合很好，可以认为本文所建立的有限元模型能够较好地模拟梁柱腹板连接在单调荷载作用下的受力性能.

图3 有限元结果与试验结果的比较

2 KI沿梁翼缘宽度的分布规律

楔形翼缘连接板腹板连接节点有限元模型见图4，材料属性同试验构件.焊缝初始缺陷深度为2.5 mm时，梁下翼缘节点焊缝应力强度因子沿梁翼缘宽度方向分布情况见图5，图中的法向拉应力σn是通过有限元积分得到的平均值.可以看出，应力强度因子KI沿梁宽度方向并不是均匀分布，KI在梁翼缘边缘最大，中部较小.这与工字钢梁与H型钢柱翼缘连接节点焊缝应力强度因子分布规律正好相反.翼缘连接，应力强度因子两边小，中间大［10］，腹板连接应力强度因子的均值较翼缘连接小［11］，腹板连接相对翼缘连接偏于安全，这与实际震害结果一致.通常情况下，梁下翼缘节点焊缝，由于梁腹板的遮挡，节点焊缝中间的初始缺陷较大.另外，焊缝的起落弧点是焊缝的关键部位，又是存在缺陷概率较大的地方，因此，焊缝中间和边缘是比较薄弱的部位.从图5可以看出，楔形翼缘连接板腹板连接节点在边缘处的应力强度因子值较仅延伸翼缘连接板腹板连接节点小，这说明采用楔形翼缘连接板可以明显改善焊缝边缘的断裂性能.为了研究方便，下面主要针对沿翼缘宽度方向的应力强度因子平均值进行研究.未注明情况下，KI指应力强度因子平均值.

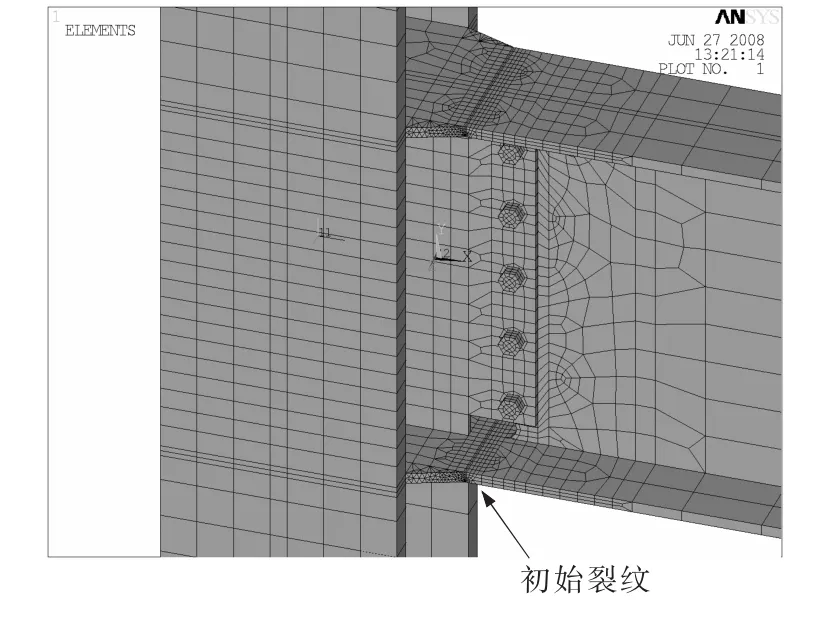
图4 楔形翼缘连接板腹板连接节点有限元模型

图5 KI沿梁翼缘宽度方向分布

3 KI沿裂缝深度变化

梁与柱节点焊缝处应力强度因子平均值KI随裂缝深度变化见图6.可以看出，无论是上翼缘还是下翼缘，受拉时应力强度因子KI都随裂纹深度增加而增大.法向应力相同的情况下，梁下翼缘焊缝断裂的可能性比梁上翼缘焊缝大得多.楔形翼缘连接板腹板连接节点的应力强度因子平均值较仅延伸翼缘连接板腹板连接节点小，这说明采用楔形翼缘连接板有助于改善腹板连接节点断裂性能.

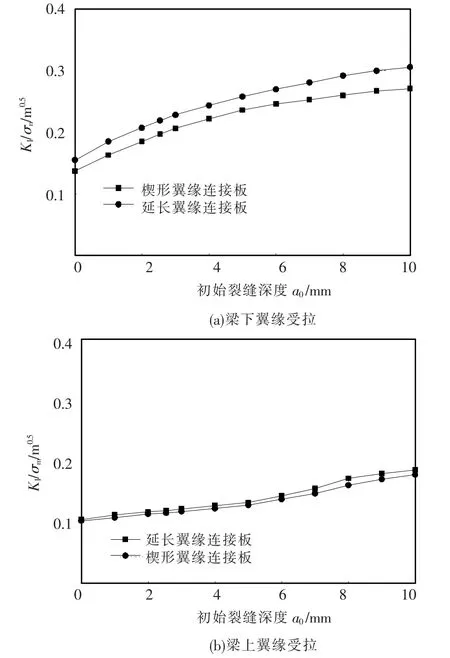
图6 KI随裂缝深度变化

梁上翼缘与柱的焊接节点，由于焊接比较方便，质量容易保证，因此，存在裂缝的可能性比下翼缘节点要小很多.在没有初始裂缝的情况下，梁上翼缘应力强度因子与法向应力的比KI/σn是0.102，北岭地震中钢结构建筑常用的E70T－4焊条断裂韧度KIC约为44～66 m0.5MPa［10］，若取KIC等于 44 m0.5MPa，那么当法向应力达到431 MPa开始起裂，而梁柱钢材的屈服强度为380 MPa，此时梁翼缘早已屈服，因此，节点就不会发生脆性破坏.这与实际震害情况是一致的，在美国的北岭地震中，很少发生腹板连接节点梁上翼缘节点焊缝断裂的情况［3］.因此，下面主要研究梁下翼缘节点焊缝断裂性能.

4 KI随各参数的变化情况

在试验构件的基础上，改变单个因素来研究该因素对KI的影响情况.研究结果表明:柱截面高度、梁和柱腹板厚度对KI/σn的影响很小，KI/σn与梁截面高度、翼缘宽度和翼缘厚度成增函数关系，与梁长度lb成减函数关系.KI/σn与柱翼缘宽度和翼缘厚度成减函数关系，与柱长度lc成增函数关系.有限元研究还发现KI/σn与梁截面参数是增函数关系，与柱截面参数是减函数关系.这是由于节点域变形对梁柱焊缝开裂有着很大的影响，节点域变形将导致梁柱节点焊缝处应力集中.任何一个梁截面参数的增大都将导致梁线刚度的提高，相对而言，节点域变弱，节点域变形增大，应力更加集中.相反，任何一个柱截面参数增大都将引起节点域刚度增大.梁长度增加，将使梁线刚度减小;柱长度增加，将使柱线刚度减小.梁柱线刚度变化将间接影焊缝处应力分布情况.

根据断裂力学知识，在均匀应力作用下，应力强度因子KI随着a0/tbf的增大而增大.由于节点焊缝处应力非常复杂，节点域变形的影响起主导作用.因此，应力强度因子KI没有随着梁翼缘厚度增加而减小.

另外，KI随着翼缘连接板伸出长度增加而减小，这是由于随着伸出长度的增加，应力沿梁翼缘宽度方向分布趋于均匀，受节点域变形影响也越来越小.

5 研究方案

为了给出KI/σn的计算公式，采用正交试验设计法进行研究方案设计［12］，由于柱截面高度、梁腹板厚度和柱腹板厚度对KI/σn的影响很小，不进行这两个参数的研究.选择正交表L32(49)，表示每个因素选用4个水平，做32次试验，最多考虑9个因素的正交表，由于本次研究正好共有9个参数.因素水平表见表2.根据对计算结果分析采用式(1)模式进行公式拟合，得到待定系数A、B、C、D和E，见式(2).公式结果与有限元结果比较见图7.应力强度因子公式最大相对误差为4.09%，公式可以较精确计算出梁柱节点焊缝应力强度因子.

表2 因素水平表

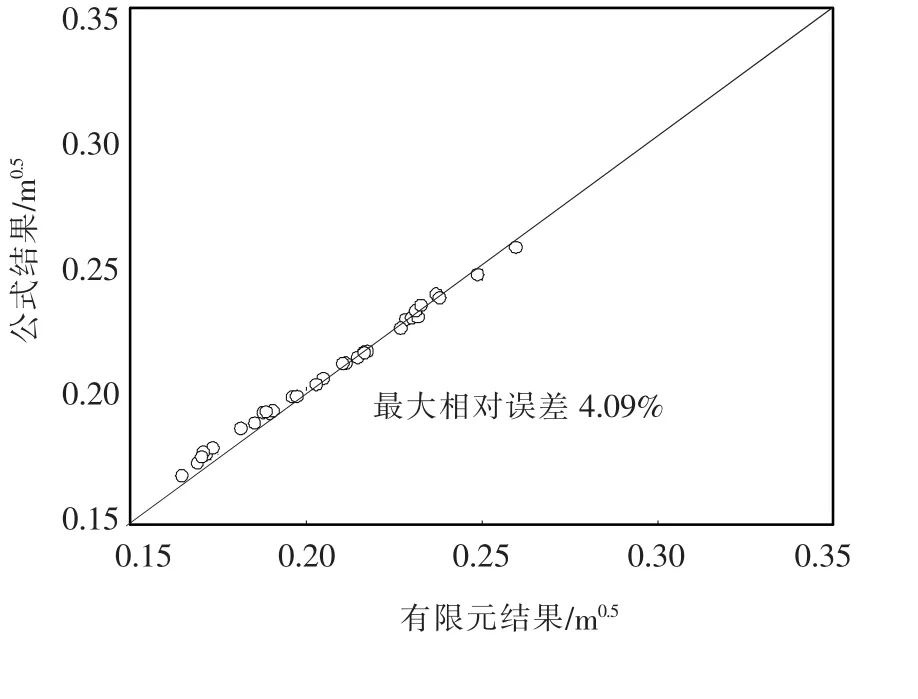
图7 公式结果与有限元结果的比较

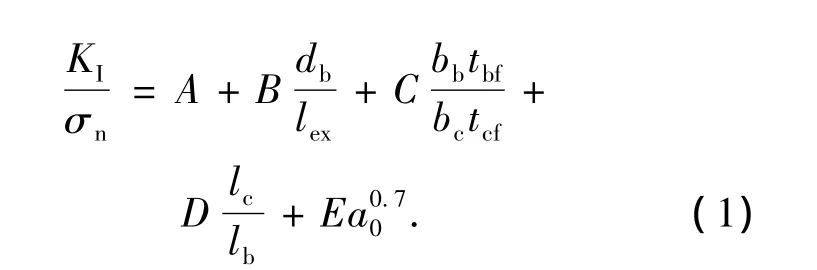
式中:bc为柱截面宽度;tcf柱翼缘厚度;db为梁截面高度bb为梁截面宽度;lex为翼缘连接板伸出长度;tbf为梁翼缘厚度;a0为裂纹的初始深度;KI为I型应力强度因子平均值;σn为法向应力.

6 结论

1)对于工字钢梁与H型钢柱腹板连接节点，应力强度因子KI沿梁宽度方向并不是均匀分布，KI在梁翼缘边缘最大，中部较小.分布规律与翼缘连接节点刚好相反，腹板连接相对翼缘连接偏于安全.采用楔形翼缘连接板可以明显改善焊缝边缘的断裂性能.

2)对于工字钢梁与H型钢柱腹板连接节点，梁上翼缘与柱的焊接节点，由于焊接比较方便，质量容易保证.研究结果表明:梁上翼缘与柱的焊接节点发生脆性破坏的可能性很小.

3)柱截面高度、梁腹板厚度和柱腹板厚度对KI/σn的影响很小，KI/σn与梁截面高度、翼缘宽度和翼缘厚度成增函数关系，KI/σn与柱翼缘宽度和翼缘厚度成减函数关系.

4)根据计算分析，拟合得到的应力强度因子公式可以较精确计算出梁柱节点焊缝应力强度因子.

［1］ HAMDY A E.A new flexibility distribution model for beam－column elements used in seismic analysis of steel frame buildings［J］.Alexandria Engineering Journal，2008，47(1):63－73.

［2］ 李国强.多高层建筑钢结构设计［M］.北京:中国建筑工业出版社，2004.

［3］ WANG Xiuli，YIN Zhanzhong，LI Qingfu，et al.Experimental study of beam－column connections with web opening in a low－rise steel frame［J］.Structural Engineering and Mechanics，2007.26(3):263－276.

［4］ VASILOPOULOS A A，BAZEOS N，BESKOS D E.Seismic design of irregular space steel frames using advanced methods of analysis［J］.Steel and Composite Structures，2008，8(1):53－83.

［5］ 王万祯，顾强.钢框架梁柱栓焊节点的有限元分析［J］.建筑结构，2002，32(9):7－10.

［6］ BINNUR G K，SECIL E.Prediction of fracture behavior of steel beam－to－column connections with weld defect using the SINTAP［J］.Engineering Structures，2005，27(5):760－768.

［7］ 郭秉山，顾强，李养成.钢框架梁柱腹板连接梁翼缘对接焊缝的破坏机理［J］.西安建筑科技大学学报，2004，24(4):417－421.

［8］ CHEN W R，LIU E M.Static web moment connections［J］.Journal of Construct Steel Research，1988，10:89－131.

［9］ CHEN W F，LUI E M.Steel beam－to－column moment connections，Part B:Web moment connections［J］.Solid Mechanics Archives，1987，12(1):1－52.

［10］ CHI W M，GREGORY G D，INGRAFFEA A.Fracture toughness demands in welded beam－column moment connections［J］.Journal of Structural Engineering，2000，126(1):88－97.

［11］ LIU Hongbo，ZHAI Changhai，SHAO Yongsong，et al.Finite element fracture mechanics study of prenorthridge connections［J］.Key Engineering Materials，2006，325:1007－1010.

［12］ KARAVASILIS T L，NIKITAS B，BESKOS D E.Behavior factor for performance－based seismic design of plane steel moment resisting frames［J］.Journal of Earthquake Engineering，2007，11(4):531－559.