三体船兴波阻力计算的自由面网格快速生成
王 中,卢晓平,王 玮
(1.海军工程大学 船舶与动力学院,湖北 武汉 430033;2.海军装备研究院 舰船所,北京 100073)
采用三维Rankine源方法计算船舶兴波阻力时,自由面网格的生成是一个必要步骤,也是一个关键步骤[1].近年来三体船成为国内外研究的热点[2-4].由于侧体的存在,自由面网格的划分比单体船更加复杂、繁琐.Dawson型方法自由面采用流线网格,三体船侧体附近的流线需要反复迭代计算、调整才能确定,费时费力;另外,更为合理的自由面条件不能完整地用流线的导数表示,如改进的Dawson法自由面条件,包括Rankine源方法各种阶次非线性自由面条件以及全非线性自由面条件.在这一类兴波阻力计算方法中,舍弃流线网格,采用自由面上的“贴水线”网格势在必行[5-6].但对三体船来说,快速生成自由面上的“贴水线”网格也并非易事.侧体以及方尾的存在使得网格生成变得相当复杂,采用商用软件(如Gambit、ICEM等)来划分此类网格固然可以解决问题,但过程繁琐,此类软件生成的网格文件必须经过进一步的解析转换才能供自己编制的兴波阻力计算程序使用.因此,针对三体船构型特点开发适用于三体船的自由面网格快速生成系统,成为提高三体船兴波问题计算效率的重要技术环节.
1 网格生成方法概述
实用的自由面网格快速生成系统应符合输入简单、修改灵活、存储方便、过程可视等要求,自由面网格快速生成系统界面如图 1所示,具备上述特点.通过该系统,可将整个输入参数及网格划分结果保存于数据文件中,需要修改时直接打开该文件,改变一些参数即可快速重新生成需要的网格;同时,可将生成的网格数据导出成文本文件,直接供其他程序使用,导出的网格文件分块存储了主区域、主体方尾后侧区域、侧体方尾后侧区域 3部分网格顶点坐标信息.
在网格划分前首先需要确定必要的信息.按如下方式定义系统的输入参数,如图 1、2所示:主体静水面水线型值点、侧体静水面水线型值点(侧体局部坐标系)及侧体横向偏距Dy和纵向偏距Dx、上游长度P1P12、下游长度P13P2、横向宽度 P1P11、倾角∠P11P1P8、纵向单位船长网格数、横向总网格数、主体与侧体间横向网格数、横向网格密度控制因子、主体方尾横向网格数、侧体方尾横向网格数,其中上游长度、下游长度、横向长度以主体长度 L为单位.

图1 软件系统主界面Fig.1 Window of the software

图2 自由面网格参数定义Fig.2 Free-surfacemesh parameter definition
如图 2所示,由输入的网格控制参数可以确定边界点:P1、P2、P3、P4、P5、P6、P7、P8、P9、P10.这些边界点与输入的船体水线型值点可生成供插值的NURBS纵向边界线:l1、l2、l3、l4、l5、l6、l7、l8、l9,参见图2.这些边界线是由一条或多条NURBS曲线组成的,不论是 2点组成的线段还是多点组成的曲线,均统一写成NURBS曲线形式,边界线可以将自由面划分成 S1~S5共 5个子区域,然后根据定义的纵向和横向网格数在各个子区域分别划分网格.NURBS曲线表示三体船自由面网格(子)区域的边界线是本文贴体坐标代数法生成自由面网格的特点之一,这种方法便于自由面网格边界线分割,从而较好地控制网格线密度.
一旦按上述方法确定了自由面网格的边界线,即可以分区采用贴体坐标代数法生成自由面网格.自由面横向网格和纵向网格密度的控制对兴波阻力Rankine源方法计算结果的影响不可忽视,在贴体坐标代数法生成自由面网格过程中可采用各种方法控制网格密度,本文纵向网格(即横向网格线)取为等间距的,重点考虑了横向网格(即纵向网格线)密度的控制.经分析和试算,确定在 l4边界以内采用较为密集的等间距横向网格,而在 l4边界以外的 S3区域采用等比数列方法控制横向网格密度,假设对一段NURBS曲线,要按照等比因子k分成N份,即将参数域u∈[0,1]按k分成N份,然后根据得到的u0、u1、u2、…、uN计算NURBS曲线上的点P(ui),根据得到的这些点即可得到网格的边界线段,如图 3所示.
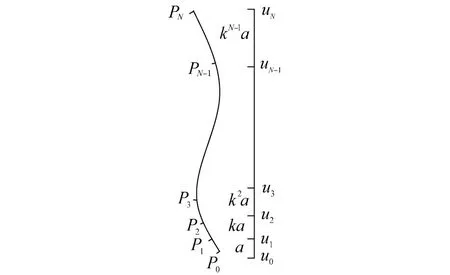
图3 NURBS曲线分段示意图Fig.3 NURBS curve subsection
设第i个分段参数变化量:
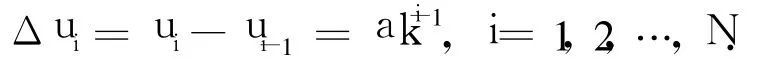
则有


由式(1)可以计算得到

以上横向网格(即纵向网格线)密度的控制是本文贴体坐标代数法生成自由面网格的特点之二.归纳以上自由面网格生成方法,可以给出本系统划分网格的流程如图4所示.
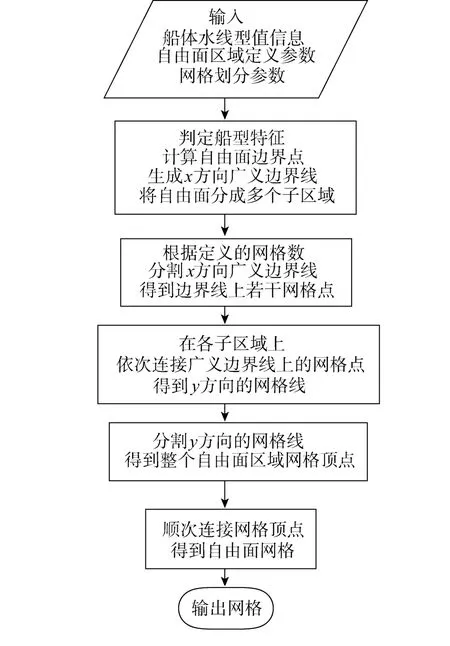
图 4 自由面网格快速生成流程图Fig.4 Flow chart of free-surface mesh generation
以上探讨的是方尾三体船型自由面网格的划分,而其他船型,如不含方尾的三体、双体、单体船型,自由面网格划分均属于它的子集,更容易生成.
2 网格生成示例
图 5所示为采用该系统生成的自由面网格,其中图5(a)是某单体方尾船型自由面网格划分软件屏幕截图,自由面计算区域参数设置与图 1相同,纵向单位船长网格数为 20,横向总网格数为 20,横向网格密度控制因子为 1.07,方尾横向划分 2个网格,总网格数为1 260.
图5(b)给出的是某5 000 t级三体船自由面网格划分截图,自由面计算区域同图1参数,纵向单位船长网格数为 30,横向总网格数为 30,主体与侧体间横向网格数为 8,倾角为 45°,横向网格密度控制因子为 1.1,半个主体方尾横向网格数为 3,侧体方尾横向网格数为 2,总网格数为 2 935.由图 5可以看出,所开发的自由面网格快速生成系统能够快速生成较复杂的自由面网格,简化了网格划分的过程;而且通过合理控制横向网格密度,节省了自由面单元数,提高了自由面网格生成效率.

图 5 自由面网格划分示例截图Fig.5 Free-surfacemesh examp les
3 数值实验
采用以上自由面网格生成方法基于Wigley数学三体船[8]实施兴波阻力数值计算,并对计算结果进行分析.Wigley数学三体船主体和侧体船型函数表达式在各自坐标系下均为
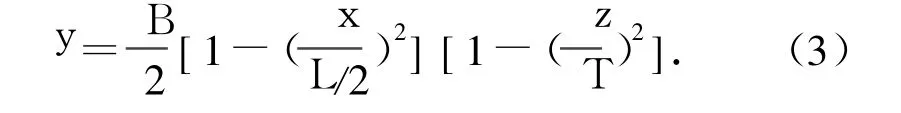
式中:L/B=10,B/T=1.6,侧体长度为中体长度的一半.根据作者们多年研究发现,当侧体位于主体中部时,不论是线性薄船理论还是Dawson型方法,都能得到与试验结果吻合较好的兴波阻力曲线,而当侧体位于主体后部时,线性薄船理论得到的结果与试验结果差别较大,因此选择这种侧体布局作为计算实例:该三体船侧体纵向偏距为0.25 L,横向偏距为0.2 L.
根据对称性,半(右)侧自由面计算区域纵向取为[-L,2L],横向取为[0,L],即自由面网格船首方向伸展0.5 L,船尾方向伸展1.5 L,船宽方向伸展L.为对比分析,采用叠模流线网格和本文方法生成的自由面网格这两类自由面网格进行计算,叠模流线网格即原始的Dawson型方法所采用的自由面网格,根据叠模计算得到的结果按流线划分自由面网格,物理量的导数采用流线上的差分来表示.
流线网格取为均匀网格,L长度内划分38个网格.由自由面叠模流线与平行于y轴的直线组成,如图6所示,各流线在起点处y方向上间隔相等.三体船侧体的存在会使得侧体内外流线 y方向上间隔不均匀,为此尽可能地保证同一宽度下各纵向位置处在y方向上的网格数接近相等,主体与侧体之间横向划分网格数为 7.船体表面与自由面保持相同的网格纵向尺度,即主体纵向划分 38个四边形网格,侧体纵向划分 19个四边形网格,主体和侧体沿吃水方向上分别划分10个和8个网格.
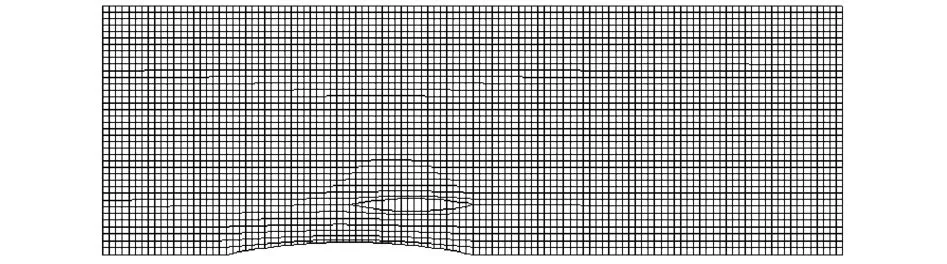
图6 流线自由面网格Fig.6 Stream line free-surfacemesh
采用本文自由面网格快速生成系统生成两种不同自由面上的“贴水线”网格进行计算,两者区别为倾角不同,一个倾角为 0°,即垂直网格(横向网格线垂直于x轴线),类似图6的流线网格;另一个横向网格线倾角为 45°,类似图 1所示网格,其他参数保持相同,即纵向单位船长网格数为 38,横向总网格数为 38,主体与侧体间横向网格数为 7,横向网格密度控制因子为 1.0.如此参数设置是尽可能与流线网格保持一致,以客观比较.
图 7给出的是兴波阻力系数计算结果与试验结果[8]的比较.图中流线网格曲线是指采用流线网格兴波阻力程序[9]根据图 6所示流线网格计算得到的结果;0°网格曲线、45°网格曲线是指采用贴体网格兴波阻力计算程序按上述贴体网格计算得到的结果,纵向导数采用迎风格式计算,横向导数采用中心差分格式计算,导数计算采用物理平面与计算平面的转换关系在计算平面上进行计算,假设计算平面坐标(ξ,η)与物理平面坐标(x,y)之间为一一对应关系:
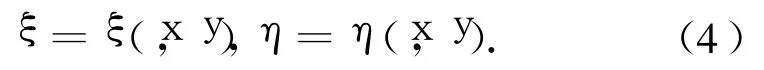
将物理空间的导数变换为对计算空间 ξ、η的导数.
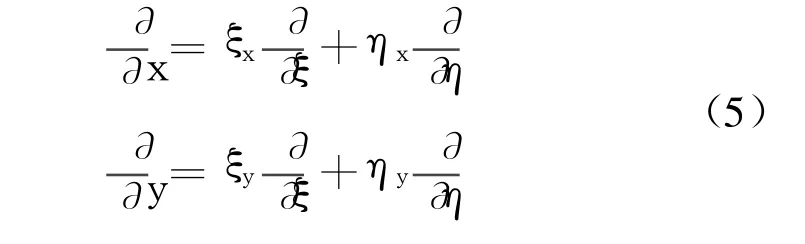
其中:
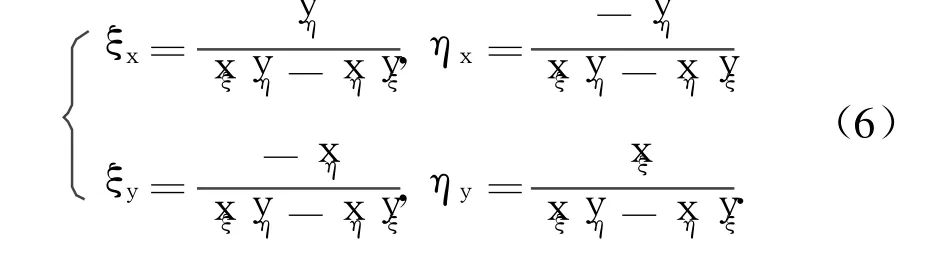
在计算平面上对自由面上物理量的导数进行计算是本文三体船兴波阻力数值计算方法的第 3个特点,如前所述,前 2个特点是自由面网格生成技术方面的特点.此外,图 7还给出了根据线性薄船理论兴波阻力计算结果[10-11]加以比较.
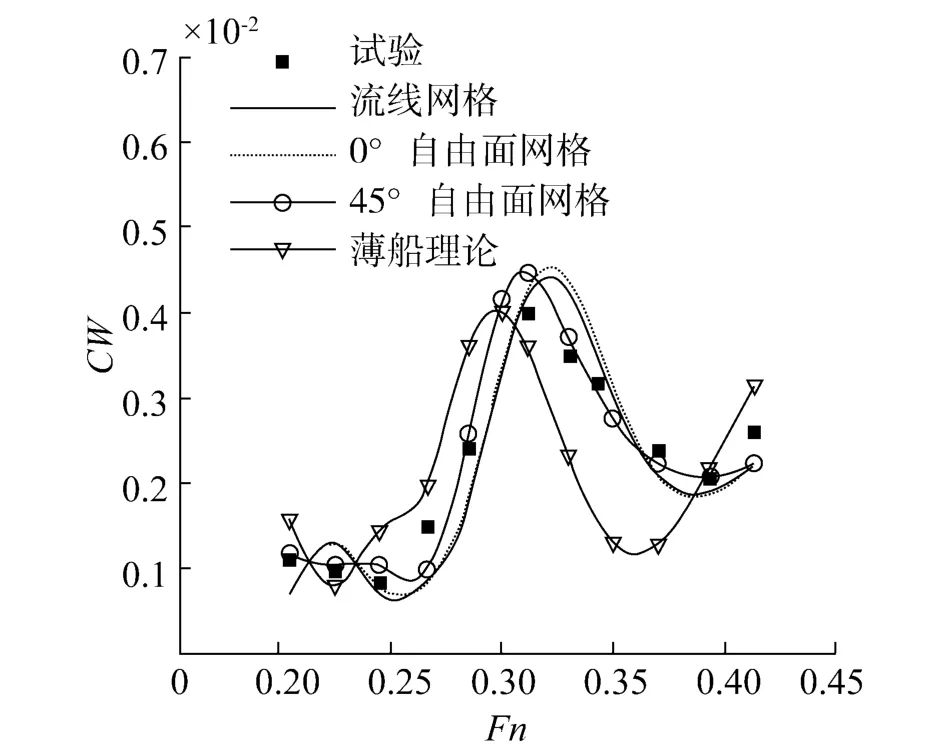
图 7 兴波阻力系数计算结果对比Fig.7 Wave drag comparison between the calculated results and experimental resu lts
从图 7可以看出,与线性薄船理论计算结果相比,线性自由面条件的三维Rankine源方法与试验结果更加接近,薄船理论结果与模型试验结果偏差较大,由于算例侧体位于主体后部,如前文所述,侧体位于主体后部,伴有较强的喷溅应该是计算结果与模型试验结果偏差的原因之一.
流线网格与 0°自由面网格计算结果差别甚微,这相互验证了流线网格、贴体网格兴波阻力计算结果的正确性,同时也说明采用自由面上的“贴水线”网格计算方法可以得到与流向网格方法一致的结果.流线网格生成费时费力,尤其是三体船兴波阻力计算过程中自由面网格生成更加复杂,由于侧体的存在,侧体两侧紧贴侧体表面的流线需要反复计算和调整才能得到,采用贴体网格预报三体船兴波阻力计算过程则较为简洁方便.
45°自由面网格计算结果与流线网格、0°自由面网格计算结果有一定差别,与试验结果比较来看似乎 45°自由面网格计算结果与试验结果更加接近,分析可能原因是 45°自由面网格更符合兴波的物理现象,但是否说明斜网格一定优于直网格尚待进一步研究.
4 结束语
作者成功开发了适用于三体船兴波阻力计算的自由面网格快速生成系统,该系统仅需简单输入必要的船体型值和几个控制参数即可快速生成三体船兴波阻力计算的自由面贴体网格,并实现网格密度变化控制,同时可应用于方尾三体船,避免了商用网格生成软件生成三体船兴波阻力计算自由面网格的繁琐过程.对一艘Wigley数学船型兴波阻力的计算说明,采用系统生成的贴体网格计算三体船兴波阻力,在计算过程简洁方便的同时还可以得出良好的计算结果.
自由面网格倾角变化对兴波阻力计算结果有一定影响,需要进一步研究.另外,方尾三体船兴波阻力的计算与非方尾船略有不同,除需要该文已实现的生成方尾后流动区域网格分块外,还需在阻力计算程序中对方尾做相应的特殊处理,这将在后续研究中考虑.
[1]高 斌,缪国平.关于Dawson方法中网格划分的研究[J].海洋工程,2000,18(1):20-28.
GAO Bin,MIAO Guoping.Investigation of grid generation in Dawson method[J].Ocean Engineering,2000,18(1): 20-28.
[2]SAUNDERS JR P.An investigation of the resistance properties of a modern trimaran combatant ship base on Taylor standard series and series64[D].CA:naval Postgraduate School,1995:1-9.
[3]卢晓平,潘雨村.高速三体船兴波阻力与片体布局优化研究[J].水动力学研究与进展(A辑),2004,19(3): 347-359.
LU Xiaoping,PAN Yucun.An investigation of wave resistance on the high speed trimarans and their piece hull position optim ization[J].Journal of Hydrodynamics(Ser A),2004,19(3):347-359.
[4]WANG Hu,ZOU Zaojian.Numerical research on wavemaking resistance of trimaran[J].J Shanghai Jiao Tong University,2008,13(3):348-351.
[5]刘应中.船舶兴波阻力理论[M].北京:国防工业出版社,2003:89-90.
[6]陈京普,朱德祥,何术龙.双体船/三体船兴波阻力数值预报方法研究[J].船舶力学,2006,10(2):23-29.
CHEN Jingpu,ZHU Dexiang,HEShulong.Research on numerical prediction method for wavemaking resistanceof catamaran/trimaran[J].Journal of Ship Mechanics,2006,10 (2):23-29.
[7]施法中.计算机辅助几何设计与非均匀有理 B样条[M].北京:高等教育出版社,2001:1-11.
[8]BATTISTIN D,DANIELLIA,ZOTTI I.Numericaland experimental investigations on wave resistanceof trimaran congurations[C]//Proceedings of the 9th International Maritime Association ofMediterranean.Ischia,Italy,2000.
[9]DAWSON CW.A practical computer method for solving ship wave problems[C]//Proc of 2nd Intl Con f on Num Ship Hydrodyn.Berkeley,Calif,1977.
[10]王 中,卢晓平,钟士岗.基于单元柯钦函数精确积分的多体船兴波阻力计算[J].哈尔滨工程大学学报, 2009,30(6):602-606.
WANGZhong,LU Xiaoping,ZHONG Shigang.Multi-hull ship wave making resistance calculation based on Kochin function integral analysis expression on the surface panels [J].Journal of Harbin Engineering University,2009,30 (6):602-606.
[11]PENG Hongxuan.Numerical computation of multi-hull ship resistance and motion[D].Halifax Dalhousie University,2001:9-38.

