一种有效的互耦阵列测向方法

祁颖松,刘章孟,周一宇

(1.中国人民解放军91550部队72分队,辽宁大连 116023;2.国防科技大学电子科学与工程学院,湖南长沙 410073)

0 引言

为了实现互耦条件下有效的阵列测向,国内外研究人员借助各种盲校正或联合估计方法,希望尽可能消除互耦效应的影响,得到了较好的效果,但多数算法的复杂度较高[1-5]。本文针对均匀线阵提出了一种有效的互耦补偿方法。新方法有效地利用了均匀线阵互耦矩阵特殊的Toeplitz结构,并忽略非相邻阵元之间相对较弱的互耦效应,通过在均匀线阵两端各增加一个辅助阵元,很好地补充了互耦效应对原始阵列各阵元接收数据之间相位偏移关系的破坏,最终得到了理想的高精度阵列测向效果。

1 常规阵列测向方法

设K个同频窄带信号从偏离法线Θ=[θ,…,θK]的方向同时入射到由M个全向阵元构成的均匀线阵上,各入射信号的功率分别为,…,,阵列接收机在t时刻的输出为:

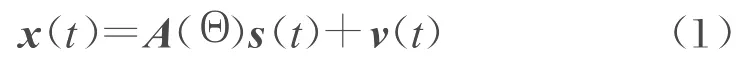
式中[A(Θ)]m,k=ej(m-1)φk为阵列响应函数,φk=2πD sinθk/λ为第k个入射信号在相邻阵元之间传播的相位延迟,D为相邻阵元间距,λ为入射信号波长,s(t)=[s1(t),…,sK(t)]T为t时刻各入射信号的波形,v(t)=[v1(t),…,vM(t)]T为t时刻阵列的观测噪声,噪声功率为且与信号相互独立。

式中N为观测数据点信号协方差矩阵。

然后对协方差矩阵作特征值分解得到正交的信号子空间U s与噪声子空间U n,

在采样点数趋于无穷大的条件下,信号子空间Us的各列与阵列响应函数A(Θ)的各列张成同样的子空间。最后通过空域搜索得到伪空间谱P(θ),

则P(θ)的K个峰值对应于各信号的入射方向。

2 均匀线阵互耦模型

各种常规阵列都难以避免地会受到互耦效应的影响,互耦效应会破坏阵列各阵元之间依赖于信号入射方向的相位偏移关系,因而会给阵列测向带来极大困难[1]。由于均匀线阵中各阵元等间隔排列,因此相邻阵元的互耦效应近似一致,且非相邻阵元间由于距离较远,其互耦效应可忽略,即均匀线阵的互耦矩阵可由下式表示[7]:

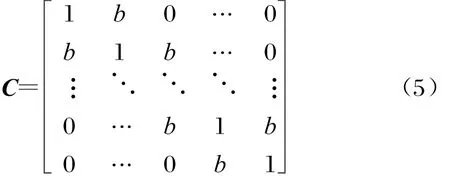
式中b为相邻阵元间的互耦系数。

考虑互耦效应之后,阵列t时刻的观测数据为:

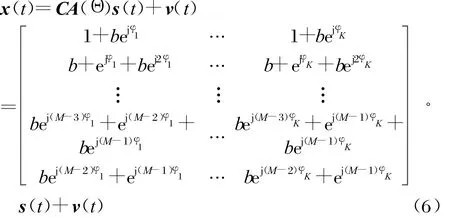
式中v(t)主要为阵列热噪声,因此受互耦效应的影响可忽略。

对比(1)式和(6)式可以发现,在考虑互耦效应的情况下,阵列各阵元接收数据之间不再具有理想的依赖于信号入射方向的相移关系,因此直接采用常规的阵列测向方法可能难以得到理想的效果。

3 均匀线阵互耦效应补偿方法

观察(6)式同时还可以看到:虽然互耦效应使均匀线阵响应函数的形式变得很复杂,但除去阵列首尾两个阵元以外,其它阵元接收数据依然满足一个确定的相位偏移关系,即:

式中[x(t)]2(M-1)表示x(t)的第2至M-1个元素。

经过以上的形式变换之后,虽然信号的幅度发生了变化,但各阵元接收信号之间的相位关系得到了较好的保留。因此,如果在原始阵列两侧各增加一个同样的辅助阵元,就能够较好地消除互耦效应在原始阵列首尾两个阵元上产生的“边缘效应”。

用T1至TM表示原始阵列阵元,T0和TM+1表示辅助阵元,则添加辅助阵元后的阵列结构示意图如图1所示。

图1 添加辅助阵元补偿互耦效应示意图

添加辅助阵元后阵元T0和TM+1上的接收数据能量同样会耦合到T1和TM两个阵元上,此时原始阵列上的观测数据可写为如下形式:

则各入射信号的阵列响应函数a(θk)(k=1,…,K)均与噪声子空间正交,通过空域搜索得到伪空间谱(θ):

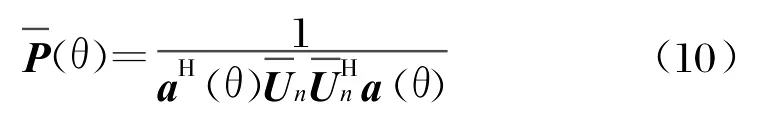
4 仿真结果

以下用特定条件下的阵列测向结果验证本文辅助阵元互耦补偿方法的有效性。

假设两个频率均为1GHz的信号分别从不同方向上入射到10元均匀线阵上,相邻阵元间距等于入射信号波长的一半,即0.15m,阵列相邻阵元之间的互耦系数b=0.4,非相邻阵元之间的互耦效应可忽略。辅助阵元法通过在原始阵列两侧各增加一个辅助阵元,用于补偿第1和第8个阵元上互耦效应与中间各阵元上互耦效应的差异。

假设两个信号的入射方向分别偏离阵列法线7°和10°,两个信号功率相等,且信噪比均为0dB,阵列接收机采样点数300。图2随机抽取了3组独立实验中互耦补偿前后的归一化空间谱图,其中图2(a)为互耦条件下常规MUSIC方法的空间谱图,图2(b)为利用本文的辅助阵元法进行互耦补偿后的空间谱图。

图2中的仿真结果表明阵列互耦效应降低了阵列对空间临近目标的分辨能力,而本文的互耦补偿方法能够较好地消除这一负面影响。

图2 互耦补偿前后对7°和10°方向入射信号的分辨效果

为了比较新方法在阵列测向精度方面的优势,将第二个信号的入射方向修改为偏离阵列法线15°,并假设两个信号功率相等,单个信号信噪比从0dB到15dB变化,采样点数300,这样常规MUSIC方法和校正后的MUSIC方法都能够较好地分离这两个信号。图3给出了互耦补偿前后由100次蒙特卡罗仿真实验得到的两种方法的角度估计均方根误差对比情况,其中图3(a)对应于第一个信号的角度估计精度,图3(b)对应于第二个信号的角度估计精度。

图3 互耦补偿前后对7°和15°方向入射信号的角度估计均方根误差

图3表明互耦条件下常规子空间测向方法无法得到一致的角度估计结果,而是始终有一个较大的偏差[6],新方法在改善常规子空间测向方法对空间临近目标分辨能力的同时,也极大地提高了其角度估计精度。

5 结束语

本文针对阵列测向效果容易受到互耦效应影响而出现性能下降的问题,结合均匀线阵互耦矩阵的特殊带状Toeplitz矩阵形式,提出了通过增加辅助阵元补偿互耦效应不利影响的方法。仿真结果表明,这种方法能在有效改善常规子空间测向方法对空间临近目标分辨能力的同时,极大地提高了其角度估计精度。■

[1] DandekarKR,LingH,XuG.Effectofmutualcouplingondirectionfindinginsmartantennaapplications[J].Electronics Letters,2000,36(22):1889-1891.

[2] Liu ZM,H uang ZT,W ang FH,et.al.DOA estimation with uniform linear arrays in the presence ofmutual coupling via b lind calibration[J].Signa l Processing,2009,89(7):1446-1456.

[3] Fabrizio S,Alberto S.A novel online mutual coupling compensation algorithm for uniform and linear arrays[J].IEEE Transactions on Signal Processing,2007,55(2):560-573.

[4] Lin M,Yang L.Blind calibration and DOA estimation w ith uniform circu lar arrays in the p resence of mutual coup ling[J].IEEE Antennas and Wireless Propagation Letters,2006,1(5):315-318.

[5] 刘章孟,黄知涛,周一宇.线性阵列互耦矩阵和波达方向的联合估计[J].电子学报,2008,36(12):2458-2463.

[6] Liu ZM,Huang ZT,Zhou YY.Bias analysis of MUSIC in the presence of mutual coup ling[J].IET Signal Processing,2009,3(1):74-84.