基于粗糙集的雷达辐射源信号识别

李 楠,曲长文,苏 峰,平殿发

(海军航空工程学院,山东烟台 264001)

0 引言

现有的辐射源识别方法主要有专家系统法[1]、神经网络法[2]、D-S推理法[3]、基于模糊集理论的识别方法、基于属性测度的识别法、基于灰色关联的识别法[4]、基于分形维数[5]的识别法等。随着雷达辐射源技术的不断发展,世界各国都使用大量常规或特殊体制的辐射源设备,配置空间逐渐扩大,配置数量大大增加。实际战场环境中,辐射源识别难以获得辐射源样本数据及识别的先验知识,不同型号的检测数据具有较大的重叠性,样本可分性差,难以达到高识别率。近来粗糙集这一新的数学理论成为信息科学领域的研究热点之一,它已经在许多领域得到了广泛应用[6-7]。

本文将粗糙集[8]用于辐射源识别中,给出了基于粗糙集的辐射源识别方法和步骤,建立了相应的模型,并将识别模型用于雷达辐射源用途识别,给出了具体的实例,结果证明基于粗糙集的辐射源信号识别是有效的,这为解决辐射源识别困难的问题指出了一条新途径。

1 粗糙集相关定义

定义1 对于一个给定的对象论域U,U上的分类族定义为一个U上的知识库,引入等价关系代替分类,当R为U上的等价关系时,则U/R为R的所有等价类族,用[x]R表示子集X属于R中的一个范畴,且R包含元素x∈U,若P⊂R,则∩P也是一个等价关系,称为P上的不可分辨关系,记作IND(P),且有

定义2 决策表S=(U,A,V,f),其中U是对象或实例的非空有限集合,A是属性的非空有限集合,A=C∪D,C∩D=φ,C为条件属性集,D为决策属性

定义3 设任一子集X∈U,R为一等价关系,则当X能被某些R基本范畴的并表示时,称子集X为R可定义集,否则称X为R不可定义集。R不可定义集是子集X上不可能恰好被定义的,也称为R不一致集或称R粗糙集,简称粗糙集。

定义4 决策表S=(U,C∪D,V,f),对于X⊆U和R⊆C,X的下近似集和上近似集分别定义为RX=

定义5 决策表S=(U,C∪D,V,f),D的C正域是论域U的所有那些使用条件类U/C所表达的知识能够正确分类到决策类U/D之中的对象的集合,记

定义6 决策表S=(U,C∪D,V,f),c∈R⊆C,若POSR-{c}(D)=POSR(D),称c在R中是可约的,否则c在R中是不可约的。若R中的每个元素都是不可约的,称R为独立的。

定义7 决策表S=(U,C∪D,V,f),R⊆C,若R是C的独立子集且POSR(D)=POSC(D),则称R为C的D约简,简称约简。

定义8 决策表S=(U,C∪D,V,f),C的所有不可约属性组成的集合称为C的核,记作core(C),它是所有约简的交,即core(C)=∩Re d(C)。

定义9 决策表S=(U,C∪D,V,f),如果k=γC(D)=card(POSC(D))/card(U),则称D是k(0≤k≤1)度依赖于C,记作C⇒k D。

2 基于粗糙集的雷达信号识别方法

针对雷达辐射源识别问题,采用粗糙集分析雷达信号数据之间的联系,获得雷达辐射源信号数据库中的重要知识和信息,提取有效的最优规则。

2.1 建立雷达辐射源识别模型

假设有m种雷达,每个雷达信号又有若干工作模式,设n为已知样本库中雷达工作模式的数目。将雷达辐射源信号特征参数看作条件属性,则条件属性集为C={c1,c2,…,cq},约简集为C*。将辐射源的类别视为决策属性,则决策属性集D={d1,d2,…,dm}。已知样本库为论域U={u1,u2,…,un},其中某一条雷达样本信息为ut={c1,t,c2,t,…,cq,t;dt}。这时研究对象ut的属性值为:ci(ut)=ci,t(i=1,2,…,q;t=1,2,…,n),d(ut)∈D。此时,由ut(t=1,2,…,n)构成的二维信息表就是关于雷达辐射源识别的关系数据模型,即S=(U,C∪D)。

2.2 连续属性离散化

粗糙集只能处理离散的属性值,实际中存在大量连续属性值,须经离散化后才能用粗糙集方法进行处理。信息表中属性分为连续型和离散型两种。连续属性离散化的方法有等间隔法、等频率法、最大熵法、神经网络法和遗传算法等。这里对不同区间数据在不影响其可分辨性的基础上进行分类,用相应符号表示。

2.3 知识约简和规则提取

利用DMRM法从决策表中提取关于属性值区分的属性构造区分函数,并且可求出属性约简和属性值约简。算法如下:(1)消去决策表中重复属性的对象xi;(2)直接从决策表中提取每个对象关于属性值是区分的属性,并构成区分函数f(k),同时利用吸收率约去多余的小析取范式,得到核属性core(C);(4)从f(k)中消去可约属性,并求出其最小析取范式f′(k),得到该对象对应的属性值约简,并由单元数范式找出核属性;(5)根据上一步结果求得包含所有约简决策规则的决策表;(6)约去所有过剩规则得到包含最小规则集的决策表;(7)提取规则集,根据核值表和原来的样本列出可能性决策表。

2.4 雷达辐射源识别过程

首先获得雷达辐射源信号数据库,而后将辐射源样本进行离散,经过粗糙集约简,最终形成可能性决策表。在此基础上,将待识别信号x0与已知信号xi的特征参数进行比较,同时将属性值用相应的符号表示,根据提取的规则集进行辐射源类别判别。

3 仿真分析

下面以雷达辐射源用途识别为例,验证本文基于粗糙集识别方法的有效性。假设雷达信号特征矢量由载频(RF)、脉冲重复频率(PFR)、脉宽(PW)等3个特征参数构成。从已知雷达库中提取3类不同用途的雷达,表1给出了已知样本特征参数。

1)对原始数据离散化,结果见表2,U={u1,u2,…,u10}表示样本对象集和,RF用a表示,PRF用b表示,PW用c表示,类别用d表示。

2)知识约简和规则提取,消去重复的属性,如表2中对象7和对象8,对象12和对象15,只取其中一个进行简化,得到简化如表3所示。

对简化表根据条件属性和决策属性的依赖关系进行约简。设R={a,b,c},则:

U/IND(R)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14}}

U/IND(R-a)={{1},{2},{3,5},{4},{6,13},{7,11,12},{8},{9,10},{14}}

表1 辐射源信号信息表

表2 离散后信息表

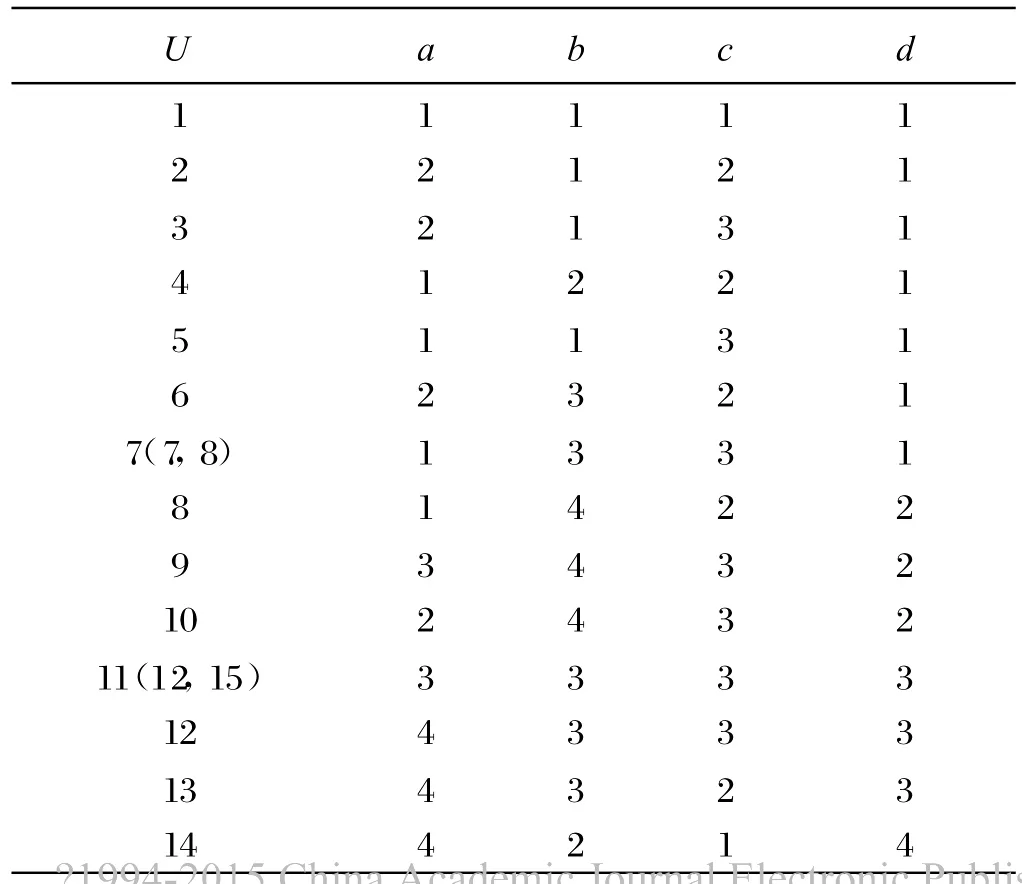
表3 离散后信息表

U/IND(R-b)={{1},{2,6},{3,10},{4,8},{5,7},{9,11},{12},{13},{14}}

U/IND(R-c)={{1,5},{2,3},{4},{6},{7},{8},{9},{10},{11},{12,13},{14}}

U/IND(R-a)≠U/IND(R),U/IND(R-b)≠U/IND(R)U/IND(R-c)≠U/IND(R)

可见a,b,c三个属性都是必要的,没有可约简的属性。从简化表提取每个对象关于属性值区分的属性,并构成区分函数。

对象1与对象9、10、11、12、13、14和16关于属性值构成的合取范式为:

f(1)=(b∨c)∧(a∨b∨c)∧(a∨d∨c)∧(a∨b∨c)∧(a∨b∨c)∧(a∨b∨c)∧(a∨b)=b

以此类推求得包含所有约简决策规则的决策表,如表4所示(“*”表示属性值可以省去)。

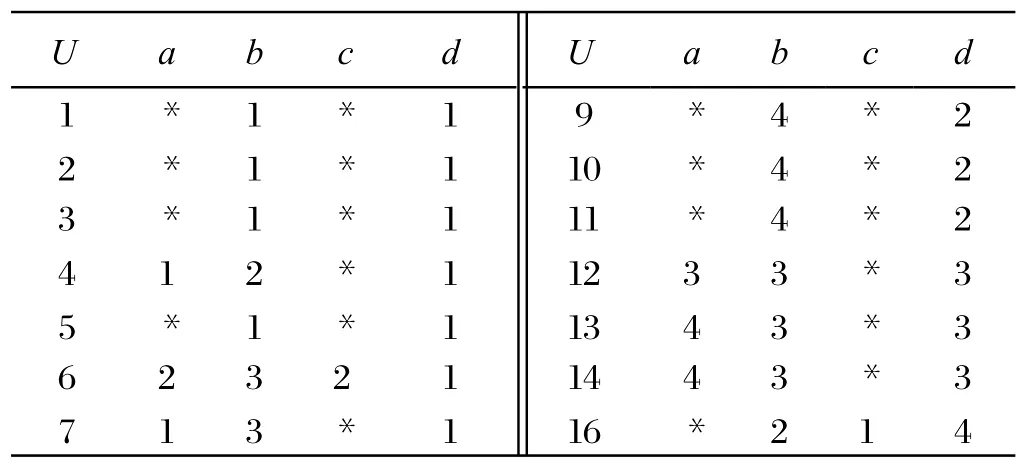
表4 约简决策表

约去所有过剩规则得到包含最小规则集的决策表,如表5所示。

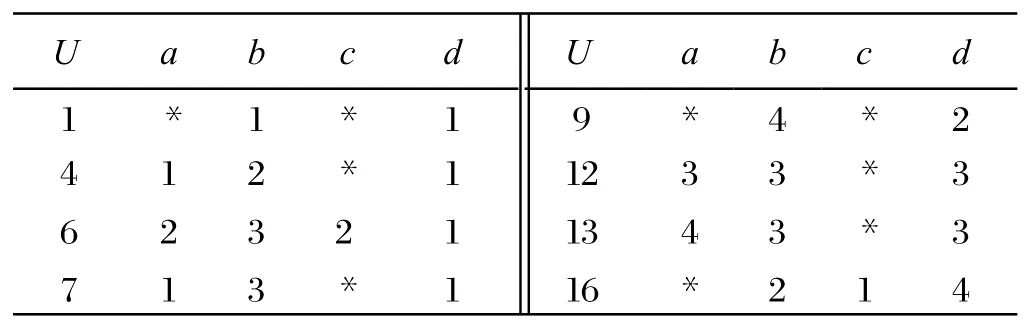
表5 最小规则集

由表4得到8条规则:第1类识别规则:b1→d1、a1b2→d1、a2b3c2→d1、a1b3→d1;第2类识别规则:b4→d2;第3类决策规则:a3 b3→d3、a4 b3→d3;第4类识别规则:b2 c1→d4。

(3)将已知样本叠加随机测量误差,然后对该信号进行侦察测量,四次观测样本如表6所示。

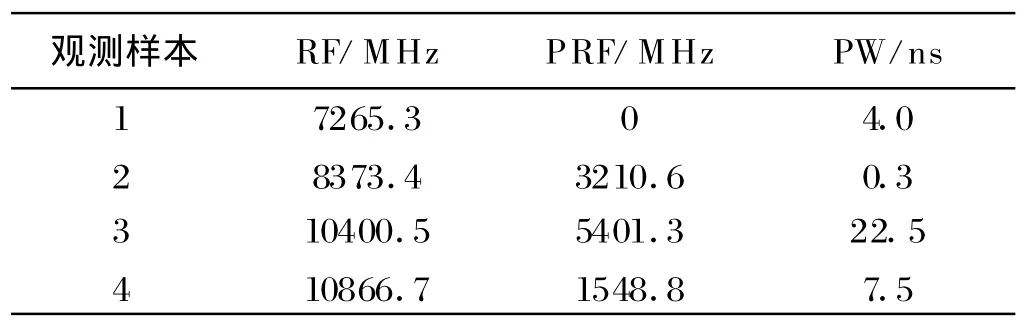
表6 观测雷达信号特征参数

采用上述的识别规则,观测信号1满足b4→d2,为第2类;信号2满足b1→d1,为第1类;信号3满足b2 c1→d4,为第4类;信号4满足a4 b3→d3,为第3类。这样就完成了辐射源信号识别。

4 结束语

本文研究了基于粗糙集的辐射源信号识别方法,针对雷达辐射源识别困难的问题,将粗糙集理论用于识别问题中,采用属性约简和属性值约简获取识别规则,建立了相应的识别模型。以雷达辐射源用途识别为例,给出了仿真分析,仿真结果验证了本文方法的有效性,为研究辐射源识别问题指出一条全新途径。■

[1] 陈锡明,祝正威,卢显良.用AUTES实现雷达辐射源识别专家系统[J].电子科技大学学报,2000,29(3):297-302.

[2] 张国柱,姜文利,周一宇.基于神经网络的辐射源识别系统设计[J].系统工程与电子技术,2004,26(2):268-272.

[3] 周旭,姜双章.雷达辐射源识别的算法研究[J].指挥控制与仿真,2007,29(5):36-40.

[4] 王杰贵,靳学明,罗景青.基于ESM与ELINT信息融合的机载辐射源识别[J].电子学报,2006,34(3):424-428.

[5] 吕铁军,魏平,肖先赐.基于分形和测度理论的信号调制识别[J].电波科学学报,2001,16(1):123-127.

[6] 陈婷,罗景青.粗集-神经网络在雷达信号识别中的应用研究[J].计算机工程与应用,2008,44(10):28-30.

[7] 庄德慧,李孝全.基于粗径向基网络的雷达信号模式识别[J].雷达科学与技术,2008,6(5):342-346.

[8] Roy A,Pal SK.Fuzzy Discretization of feature space for a rough set classifier[J].Pattern Recognition Letters,2003(24):895-902.